Modellieren von Rundspantrümpfen
C-spline Lofted Surface und die Vertexkurven-Methode
von Reinhard Siegel

Einleitung
Dieser Artikel beschreibt an Hand des Modells sy15.ms2 die bevorzugte Methode des Autors, in MultiSurf die Rumpffläche eines Rundspantbootes zu modellieren. Dabei geht es nicht um einen Rumpf mit spezifischen Abmessungen oder Formmerkmalen, sondern es soll eine in der Praxis erprobte Vorgehensweise gezeigt werden, so daß man am Ende das auf dem Bildschirm sieht, was man sich vorgestellt hat.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point)
Mc: Masterkurve, Stützkurve (master curve, support curve)
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
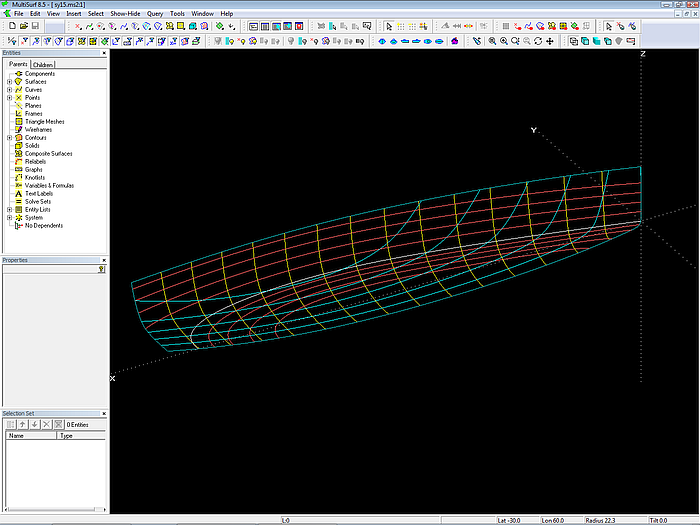
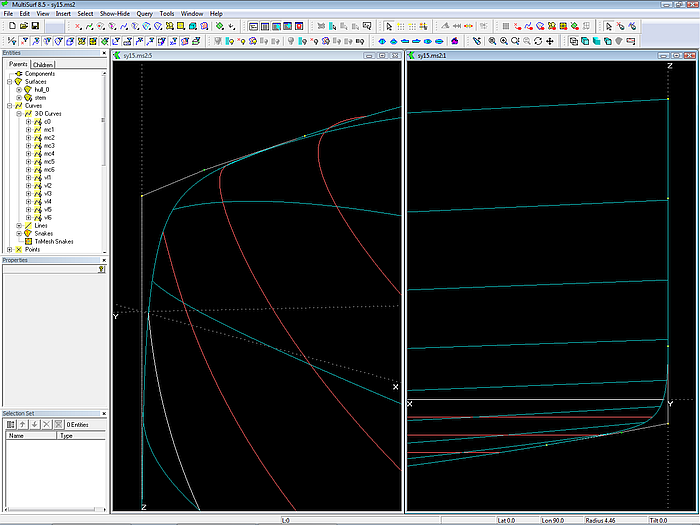
Modell sy15.ms2. Die Anordnung der Manager-Fenster und Werkzeugleisten ergibt eine möglichst große Zeichenfläche in MultiSurf.
Wird das Modell sy15.ms2 in MultiSurf geöffnet, werden für einen 15 m langen Rundspantboot der Umriß des Rumpfes, Spanten, Wasserlinien und Schnitte angezeigt.
Die für den Rumpf verwendete Flächenart ist eine C-spline Lofted Surface.
Warum C-spline Lofted Surface?
Die Rumpfform legt es nahe: sie ist in Längsrichtung wenig gekrümmt und weist keine Unstetigkeit auf. Eine C-spline Lofted Surface ist analog zu einem als Karweel-, Klinker- oder Leistenbau hergestellten Rumpf. Bei diesen Bauweisen wird ein Mallengerüst (Vorsteven, einige Spanten, Spiegel) mit Planken belegt. Bei einer C-spline Lofted Surface sind die Mallen die Masterkurven (Stützkurven), die mit C-spline Curves (kubische Splines) "beplankt" werden. Ein kubischer Spline ist das mathematische Modell einer Straklatte; seine Stützpunkte (die Punkte, durch die er verlaufen soll) entsprechen den Strakgewichten, mit denen die Latte auf dem Zeichentisch festgehalten wird. Ein kubischer Spline verläuft immer durch alle Stützpunkte.
Hinweis: läßt sich die Fläche gut mit Leisten beplanken --> C-spline Lofted Surface
Eine C-spline Lofted Surface verläuft immer durch ihre Stützkurven (Masterkurven, Mcs). Die "Planken" werden direkt an ihnen "befestigt". Darum liegen alle Mcs in der Fläche und nicht ganz oder teilweise außerhalb - so wie die Mc aussieht, so sieht der Rumpf an dieser Stelle aus.
Hinweis: soll die Oberfläche durch die Mcs verlaufen --> C-spline Lofted Surface
Die Rumpffläche wird von 6 Masterkurven gestützt.
Warum 6 Masterkurven?
Wieso nicht 3 oder 4 Masterkurven? Die Anzahl der Masterkurven hängt davon ab, an wievielen Stellen man eine Straklatte festhalten müßte, um den beabsichtigten Verlauf entweder der Oberkante (in Seitenansicht und Aufsicht)) oder der Unterkante (Bodenkontur) der Rumpffläche zu zeichnen. Je geringer die Anzahl der Mcs, umso geringer ist die lokale Kontrolle der Form, und umso mehr muß man akzeptieren, was die Latte „will“. Die Erfahrung zeigt, daß ein guter Kompromiß zwischen Einfachheit (wenige Mcs) und hinreichendem lokalem Einfluß bei 6 Mcs liegt.
Hinweis: die Randkurve (Oberkante Rumpf, Bodenkontur) mit der kompliziertesten Form bestimmt die Anzahl der Mcs sowie ihre Position in Längsrichtung.
Mitunter ist auf Grund der gewünschten Lage des Verdrängungsschwerpunktes der Verlauf der Bodenkontur komplexer als die Form der Rumpfoberkante.
6 Mcs sind kein Dogma. Wenn man die gewünschten Verlauf von Rumpfoberkante und Boden mit weniger Mcs erreichen kann, nimmt man weniger. Wenn 6 Mcs zu wenig sind, versucht man es mit 7 oder 8 Mcs.
Alle Mcs der Rumpffläche im Modell sy15.ms2 sind B-spline Curves.
Warum B-spline Curve als Stützkurve?
Der Rumpf ist in Querrichtung (Spantrichtung) sehr viel stärker gekrümmt als in Längsrichtung. Eine B-spline Curve ist mit wenigen Kontrollpunkten (Cps) leicht zu formen. Bis auf den ersten und den letzten Cp verläuft sie nicht durch ihre Kontrollpunkte, die Kurvenform ähnelt aber dem Polygonzug durch ihre Kontrollpunkte. Die B-spline Curve beginnt immer tangential zur Linie zwischen dem 1. und 2. Cp und endet immer tangential zur Linie zwischen dem vorletzten und letzten Cp. Diese Tangentialeigenschaft ist sehr nützlich für die Konstruktion eines strakenden Übergangs zwischen 2 Kurven oder 2 Flächen. Auch ein vertikaler Start oder ein horizontales Ende des Kurvenverlaufs ist mit einer B-spline Curve leicht zu bewerkstelligen. Im ersten Fall müssen cp1 und cp2 die gleiche Y-Koordinate haben, im zweiten Fall müssen vorletzter und letzter Kontrollpunkt die gleiche Z-Koordinate haben.
Alle B-spline Curves im Modell sy15.ms2 haben den gleichen Grad (degree) und die gleiche Anzahl von Cps.
Warum gleicher Grad und gleiche Anzahl von Cps?
Die Rumpffläche wird ja als C-spline Lofted Surface erzeugt - das heißt, die Mcs werden mit C-spline Curves "beplankt". Dabei geht das "Beplanken" wie folgt vor sich: durch den ersten Punkt jeder Mc wird eine C-spline Curve gelegt; das ergibt die Oberkante des Rumpfes. Dann wird auf jeder Mc ein weiterer Kurvenpunkt berechnet, der ein bißchen tiefer liegt als der vorangehende, und durch diese Punkte wird die nächste C-spline Curve gelegt. Diese Prozedur wird solange fortgesetzt, bis die letzte Kurve durch den Endpunkt von jeder Mc verläuft (Bodenkontur). Mit anderen Worten: immer in Kontakt mit den Mcs wandert eine Straklatte von oben bis unten entlang der Mcs und überstreicht so ein Fläche im Raum.
Betrachtet man einen karweel gebauten oder geklinkerten Rumpf, dann sieht man, daß alle Planken in harmonischer Form vom Bug zum Heck verlaufen.
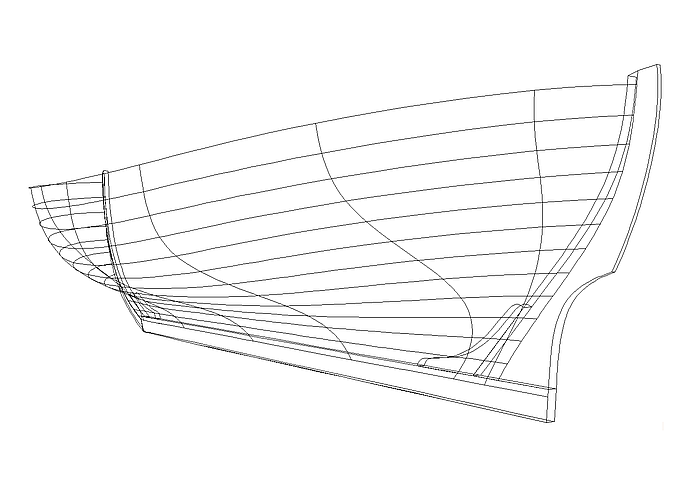
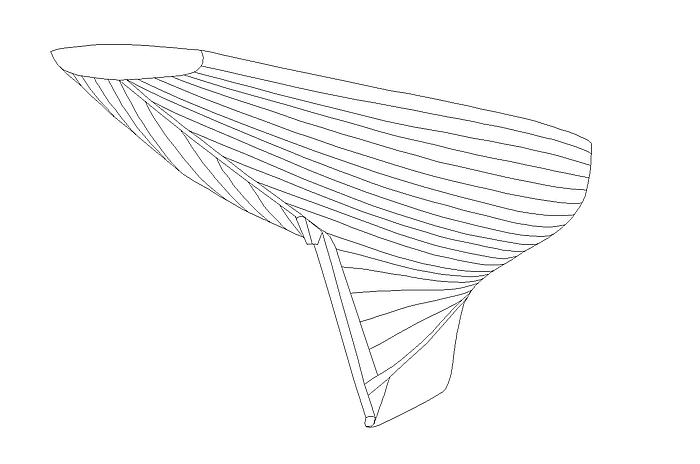
Diesen Planken entsprechen bei einer C-spline Lofted Surface die in Längsrichtung verlaufenden Parameterkurven (u-konstant) der Fläche. Um nun eine glatte, strakende C-spline Lofted Surface ohne ungewollte Unregelmäßigkeiten zu erzeugen, sollten diese u-Parameterkurven ebenfalls auf harmonische, regelmäßige Weise verlaufen. Das erfordert, daß die Abfolge der Kurvenpunkte auf den Mcs harmonisch verteilt ist. Bei Kurven vom Typ B-spline Curve ist das nur dann der Fall, wenn ihr Grad und die Anzahl der Cps gleich ist.
Warum 6 Cps?
Je mehr Cps verwendet werden, umso größer ist die lokale Kontrolle über die Form der Masterkurve. Andererseits nimmt der Aufwand zu, um die Cps so zu positionieren, daß eine harmonisch gekrümmte Kurve mit dem gewünschtem Verlauf entsteht. Die Erfahrung zeigt, daß 6 Cps ein guter Kompromiß sind zwischen Einfachheit (wenig Cps) und genügend lokalem Einfluß.
6 Cps sind kein Dogma. Läßt sich die gewünschte Form der Mcs mit weniger Punkten erreichen, nimmt man weniger. Wenn 6 Cps nicht ausreichen, muß man es mit 7 oder 8 versuchen.
Hinweis: die Mc mit dem kompliziertesten Verlauf bestimmt die Anzahl der Cps an allen Mcs.
Warum liegen bis auf den Bug alle Mcs in Spantebene?
Wenn bei einer C-spline Lofted Surface eine Mc ganz in Spantebene verläuft, dann ist die Form der Mc gleichzeitig auch Spantform. Das heißt, in X-Ansicht zeigt die Mc die wahre Rumpfform, und so haben wir einen unmittelbaren Zusammenhang zwischen der Anzeige der Mc auf dem Bildschirm und der Rumpfform: was man sieht, das bekommt man.
Mcs in Querschiffsrichtung sind kein Dogma. In stark gekrümmten Bereichen des Rumpfes, wie dem Vorschiff eines Motorbootes oder dem Heck eines Spitzgatters, kommt man ohne schräg angeordnete Mcs, die die Fläche besser stützen, nicht aus. Wo es diese Notwendigkeit nicht gibt, sind Mcs in Spantebene zu bevorzugen.
Alle korrespondierenden Cps der Mcs sind mit C-spline Curves als Vertexkurven verbunden.
Warum Vertexkurven?
Die Aufgabe besteht nicht nur darin, eine Fläche von gewünschter Größe und Form zu modellieren, die Fläche muß auch glatt sein, straken. Ähnlich wie bei einem realen Rumpf in Klinker-, Karweel- oder Leistenbauweise mit seinen strakend verlaufenden Planken ist eine C-spline Lofted Surface dann glatt, wenn ihre u-Parameterkurven (ihre "Planken") auch straken.
Wenn bei einer C-spline Lofted Surface alle Mcs als B-spline Curves vom gleichen Grad und gleicher Anzahl von Cps definiert werden, dann besteht ein enger Zusammenhang zwischen dem Verlauf ihrer u-Parameterkurven und dem Verlauf dieser Vertexkurven. Sie zeigen, wie sich die Position einander entsprechender Cps vom Bug zum Heck hin verändert. Verlaufen die Vertexkurven regelmäßig, ist die Fläche glatt.
Hinweis: strakende u-Parameterkurven sind Kennzeichen einer glatten Fläche.
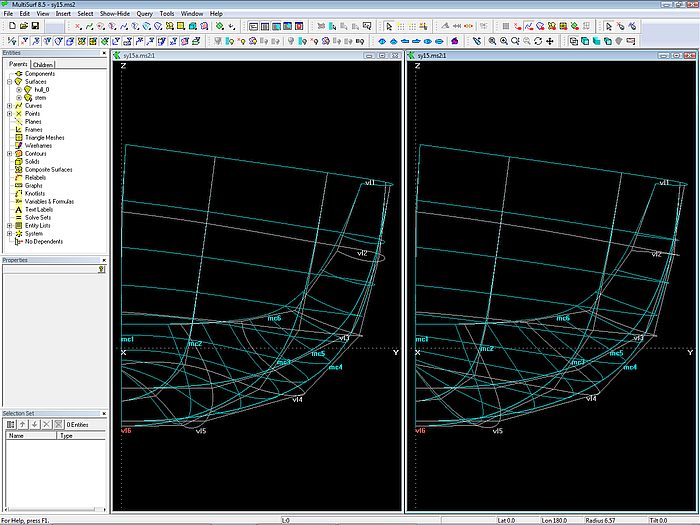
Bei einer C-spline Lofted Surface besteht ein enger Zusammenhang zwischen dem Verlauf ihrer u-Parameterkurven und dem Verlauf der Vertexkurven.
Die Vertexkurven-Methode
Unter der Voraussetzung, daß Kurventyp, Grad und Anzahl der Cps ist bei allen Mcs gleich ist, gilt:
- strakende Vertexkurven ergeben strakende u-Parameterkurven
- strakende u-Parameterkurven kennzeichnen eine strakende Fläche
- strakende Vertexkurven ergeben eine strakende Fläche
Vertexkurven sind also Hilfskurven zum Straken einer C-spline Lofted Surface. Sie machen deutlich, wie sich die Position der Cps von Bug zum Heck hin entwickelt. Verlaufen sie in harmonischer, regelmäßiger Weise, dann ist die Fläche glatt.
Eine der Voraussetzungen für die Vertexkurven-Methode - alle Mcs müssen die gleiche Anzahl von Cps haben - erzwingt, daß die Mc mit der kompliziertesten Form die notwendige Anzahl der Cps bestimmt. Obwohl andere Mcs für den Rumpf mit weniger Punkten definiert werden könnten, müssen wir die erforderliche höhere Anzahl verwenden.
Dieser Nachteil wird mehr als aufgewogen durch die Möglichkeit, mit der Vertexkurven-Methode schnell und visuell verständlich den Strak einer C-spline Lofted Suface zu kontrollieren.
Die Modellieraufgabe hat also zwei Seiten - man muß die Cps an allen Mcs so anordnen, daß sich die gewünschte Rumpfform ergibt und gleichzeitig die Vertexkurven einen strakenden Verlauf annehmen.
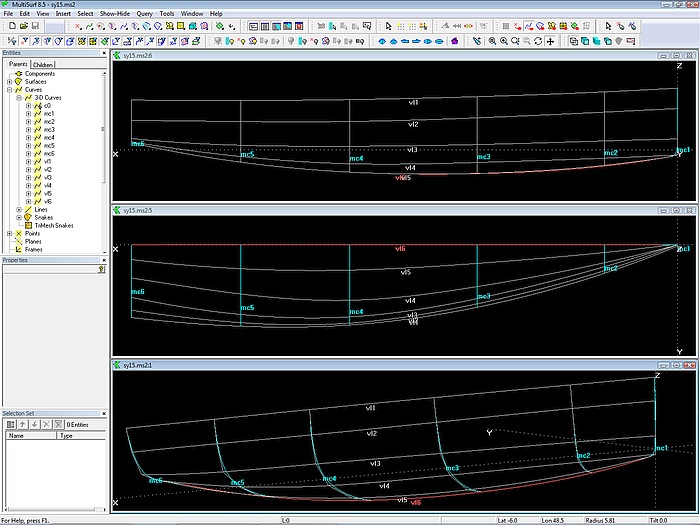
Vertexkurven als Strakhilfe
Es sei betont, daß unregelmäßige u-Parameterkurven nicht zwingend ein Anzeichen dafür ist, daß die Fläche nicht strakt.
Hinweis: auch wenn die u-Parameterkurven nicht straken, kann die Fläche dennoch glatt sein.
Man stelle sich einen glatten weißen Rumpf vor, auf den mit schwarzem Stift Längskurven gemalt werden. Wie krumm diese auch immer sein mögen, der Rumpf bleibt glatt.
Das Modellieren von Rümpfen nach der Vertexkurven-Methode ist jedoch viel einfacher und schneller, als bei unähnlichen Mcs (weil unterschiedlich im Typ, Grad oder Anzahl der Cps) durch Relabeln zu versuchen, regelmäßig verlaufende u-Parameterkurven zu erzeugen, oder ständig zu prüfen, ob die Fläche nicht trotzdem glatt ist, obwohl die u-Parameterkurven nicht straken.
Vertexkurve vl1 verläuft durch alle Cps Nr. 1 der Mcs. Sie ist identisch mit der Oberkante der Rumpffläche. Vertexkurve vl6 verläuft durch alle Cps Nr. 6 der Mcs. Sie ist identisch mit der Unterkante der Rumpffläche, also der Bodenkontur.
Warum in 3D straken?
Die Rumpfoberfläche muß glatt sein. Die Vertexkurven-Methode besagt: straken die Vertexkurven, dann strakt die Fläche. Folglich müssen die Cps der Mcs so angeordnet werden, daß die Vertexkurven glatt verlaufen. Das läßt sich sehr gut kontrollieren, in dem man sich diese Strakhilfskurven in 3D-Ansicht ansieht. Das Modell läßt sich auf dem Bildschirm um jeden beliebigen Punkt drehen, so daß man schräg entlang jeder Kurve schauen kann. Genau so, als hätte man ein echtes Modell gebaut und würde es in seiner Hand hin und her bewegen. Auf diese Weise läßt sich jede Unregelmäßigkeit im Verlauf einer Kurve, einer Wasserlinie etc. feststellen.
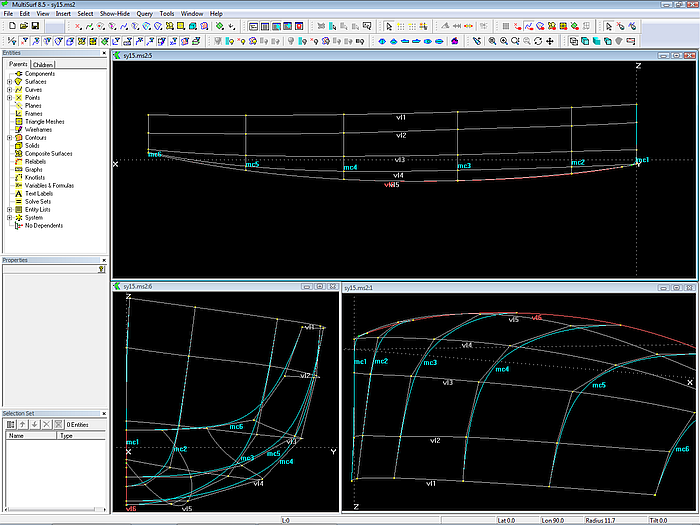
In der 3D-Ansicht läßt sich auf einfache Weise feststellen, wenn Kurven nicht straken. In der Seitensicht ist die leichte Delle der Vertexkurve vl2 nahe mc2 schwer zu erkennen. Vertexkurve vl4 verläuft unähnlich zu vl3 und vl5.
Warum das Verschieben von Cps einschränken?
Verschiebt man einen Kontrollpunkt einer Masterkurve in der 3D-Ansicht, ändern sich alle seine 3 Koordinaten gleichzeitig. Über die Eigenschaft "Dragging" bei Punkten kann dies verhindert werden. Zwei Beispiele:
Um sicherzustellen, daß alle Cps von mc2 bis mc6 in ihren Spantebenen bleiben, ist ihre "Dragging"-Eigenschaft auf (y and z) gesetzt. Wenn nun diese Punkte in 3D verschoben werden, ändern sich ihre X-Koordinaten nicht.
Mc4, mc5 und mc6 sollen senkrecht zur Mittschiffsebene enden. Diese Eigenschaft wird fest verdrahtet, in dem der vorletzte Cp (hier cp5) relativ zum letzten Cp (cp6) definiert ist, mit dz = 0. Um diese geometrische Beziehung beim Punkteverschieben zu bewahren, ist sein "Dragging" gesetzt auf (y). Somit läßt sich cp5 zwar horizontal verschieben, aber nicht vertikal. Da sein Bezugspunkt (cp6) immer auf der Mittschiffsebene liegen muß, wird diesem nur Bewegung in Z-Richtung erlaubt (Dragging: (z)).
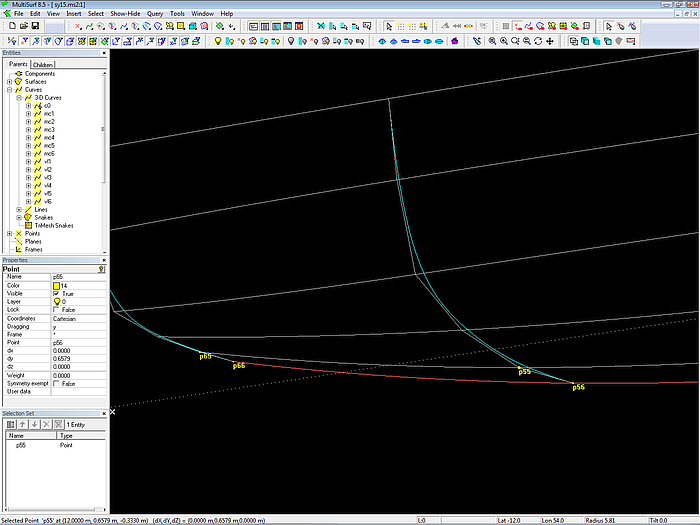
Die Punkte p55 und p65 sind relativ zu den Punkten p56 und p66 definiert. Setzt man die "Dragging"-Eigenschaft von p56 und p66 auf (z) und die von p55 und p65 auf (y), können alle Punkte in der 3D-Ansicht bewegt werden, ohne daß sich die geforderte geometrische Beziehung ändert (die Mcs sollen normal zur Mittschiffsebene enden).
Warum so und nicht anders?
Anstatt die Punkte cp5 der letzten 3 Mcs relativ zu cp6 zu definieren, könnte man auch cp6 als Projected Point von cp5 auf die Mittschiffsebene erzeugen. Dann hätten die Cps 5 und 6 auch immer die gleiche Z-Koordinate, und folglich würden die B-spline-Masterkurven immer exakt senkrecht auf der Mittschiffsebene enden.
Angenommen, es würde so gemacht. Und wir setzen Dragging von cp5 auf (y and z). Nun wollen wir diesen Punkt etwas weiter weg von der Mittschiffsebene bewegen, das heißt, seinen Y-Koordinatenwert ändern bei Beibehaltung des Z-Wertes. Also setzen wird sein Dragging auf (y) und verschieben ihn. Aber wenn wir später den Punkt in nur Z-Richtung schieben wollen, muß die Dragging-Einstellung wieder umgestellt werden. Darum muß ständig die Einstellung von Dragging verändert werden, wenn wir nicht wollen, das sich beide Koordinatenwerte ändern, wenn der Punkt in der 3D-Ansicht bewegt wird. Das ist einfach sehr umständlich.
Warum muß man auf den Verlauf von vl5 und vl6 achten?
Ab mc4 sollen alle Mcs normal (senkrecht) zur Mittschiffsebene enden. Darum haben jeweils ihre cps 5 und 6 die gleiche Z-Koordinate. An der Position dieser Mcs verlaufen also vl5 und vl6 in Y-Ansicht übereinander. Aber auch zwischen den Mcs müssen beide Vertexkurven in der Seitenansicht übereinander liegen. Ansonsten würde eine positive oder negative Aufkimmung der Rumpffläche entstehen. Deswegen muß man dafür sorgen, daß in der Seitenansicht vl5 und vl6 von mc4 an genau übereinander verlaufen.
Wie macht man das?
Man wähle cp5 von mc3 aus (Name im Modell sy15.ms2: "p35"). Dann wählt man die Y-Ansicht aus und zoomt tief in den Bereich zwischen mc4 und mc5. Nun prüft man, ob vl5 über oder unter vl6 verläuft. Falls dies der Fall ist, und cp5 von mc3 immer noch ausgewählt ist, ändert man im Properties-Manager seine Z-Koordinate, bis beide Vertexkurven zusammenfallen. Oftmals handelt es sich um Änderungen in der Z-Koordinate von Cp5 an mc3 in der Größenordnung von 1/10 Millimeter.

Bei starker Vergrößerung der Anzeige lassen sich sehr kleine Ungenauigkeiten feststellen und korrigieren.
Hinweis: mit Hilfe des Properties-Managers lassen sich die Koordinaten eines Punktes ändern, der nicht im Anzeigebereich liegt.
Auch in der Render-Ansicht kann man kontrollieren, ob die Fläche im Hinterschiff einen First oder Einschnitt hat.
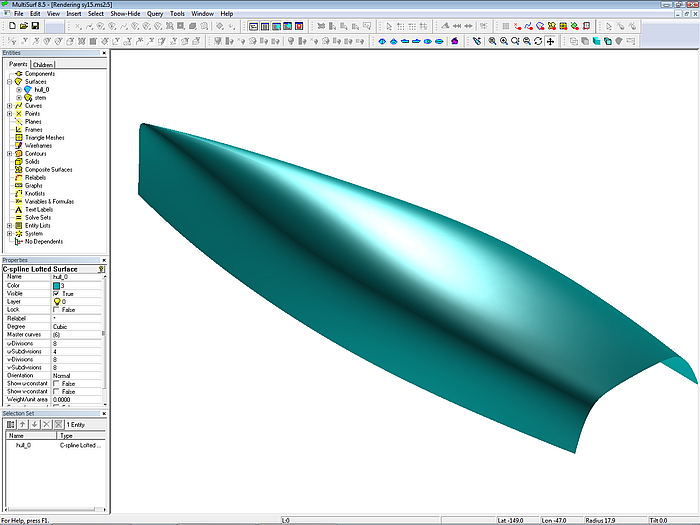
Überprüfen der Aufkimmung im Hinterschiff in der Render-Ansicht
Warum man auf den Einlauf der Bug-Mc in die Bodenkontur achten sollte
Die Vertexkurve vl6 beschreibt die Bodenkontur des Rumpfes. Die Bug-Mc muß ohne Knick in den Boden einlaufen (es sei denn, dies wäre Absicht). Das läßt sich leicht in 3D-Ansicht überprüfen. Dazu wählt man zuerst cp6 von mc1 aus, gefolgt vom Befehl "Zoom to Selection", um cp6 zum Mittelpunkt der Drehung zu machen, abschließend durch Zoomen und Drehen die Ansicht so einstellen, daß man schleifend entlang dem Ende von mc1 und dem Anfang von vl6 blickt.
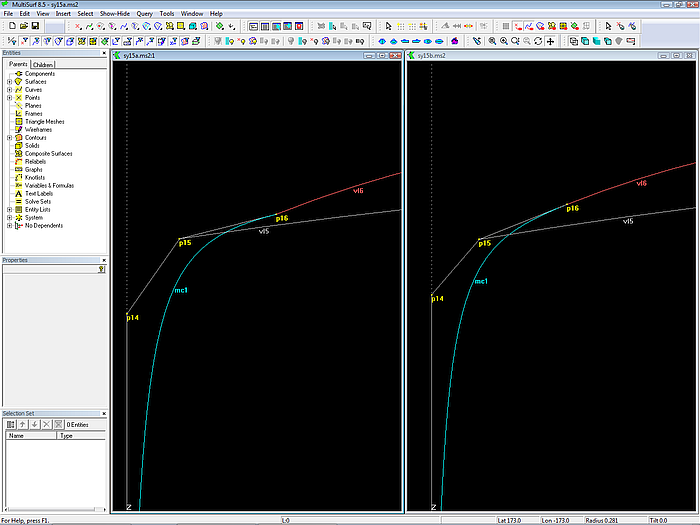
In einer 3D-Ansicht läßt sich ein Knick zwischen Bug-Mc und Bodenkontur (vl6) leicht feststellen.
Beide Kurven treffen sich dann ohne Knick, wenn die Richtung der Tangente am Ende der Bug-Mc mit der Richtung der Tangente am Beginn der Vertexkurve vl6 übereinstimmt.
Gibt es einen Knick, kann man dies manuell beheben durch Verschieben von cp5 oder cp6 von mc1 in Z-Richtung, bis es für die Genauigkeit beim Bau der Großausführung hinreichend glatt aussieht.
Dies ist jedoch keine dauerhafte Lösung. So wie etwas an der Form der Bug-Mc oder dem Verlauf der Bodenkontur geändert wird muß man den Übergang zwischen beiden Kurven erneut prüfen und gegebenenfalls wieder korrigieren.
Man löst das Problem in MultiSurf dauerhaft besser folgendermaßen. Wobei wir uns erneut die Tangentialeigenschaft von B-spline-Kurven zu Nutze machen. Zuerst benötigen wir eine Linie, die zu vl6 im Anfangspunkt tangential ist. Dazu erzeugen wir auf vl6 einen Bead mit t=0, darauf basierend einem Tangent Point und zwischen beiden eine Line. Dann setzt man einen Bead auf diese Tangentenlinie und ersetzt damit cp5 der Bug-Mc. Mit dieser einfachen geometrischen Konstruktion ist der tangentiale Einlauf der Bug-Mc in die Bodenkontur des Rumpfes im Modell fest verdrahtet.
Hinweis: geforderte geometrische Beziehungen sollten fest eingebaut werden.
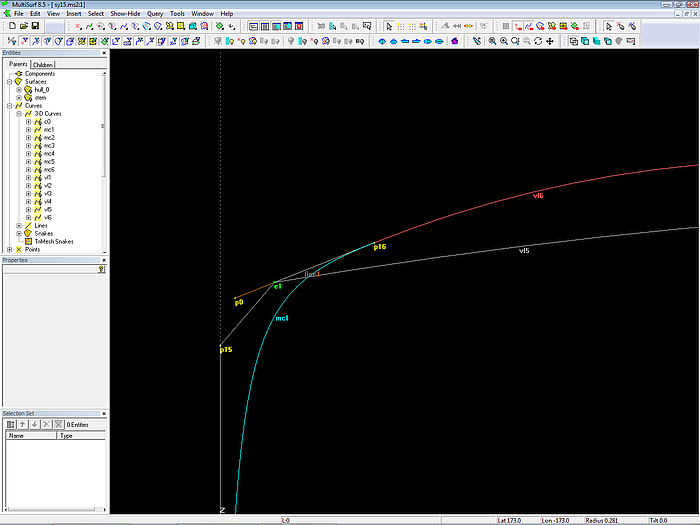
Fest verdrahteter tangentialer Übergang zwischen Bug und Bodenkontur
Warum liegt die letzte Mc hinter dem Spiegel?
Die Rumpffläche ist etwas länger als das tatsächliche Boot. Das heißt, der Rumpf soll an einem Spiegel getrimmt werden. Wenn man die letzte Mc als Snake (Flächenkurve) auf der Spiegelfläche erzeugt, um sich das Trimmen des Rumpfes zu sparen, dann sollte man bedenken, daß die Rumpffläche sich unvermeidlich ändern wird, wenn der Spiegel in Position, Neigung oder Form modifiziert wird. Häufig kommen solche Änderungswünsche in letzter Minute.
Man baut Unabhängigkeit in das Modell ein, wenn man nicht so vorgeht. Dann kann die Spiegelfläche geändert werden, ohne daß es Einfluß auf die Rumpfform hat. Gibt es einen plausiblen Grund, warum sich die Rumpfform ändern sollte, wenn man Neigung, Radius oder Position des Spiegels ändert?
Hinweis: keine unnötigen Abhängigkeiten einbauen.
Wie man hohle Wasserlinien beseitigt
Bei einem Rumpf, dessen Vorsteven mit starker Krümmung in die Bodenkontur einläuft, sind die Wasserlinien im Bugbereich oft hohl. Das ist kein Naturgesetz beim rechnergestützten Schiffsentwurf.
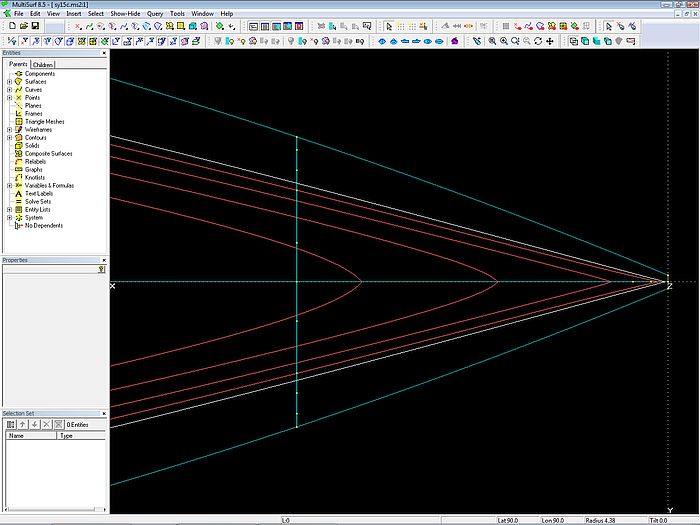
In der Aufsicht (Z-Ansicht) läßt sich nicht erkennen, ob Wasserlinien hohl verlaufen.
In der Z-Ansicht sind hohle Wasserlinien nicht zu erkennen. Besser ist es, den Wasserlineneintritt in der 3D-Ansicht zu kontrollieren.
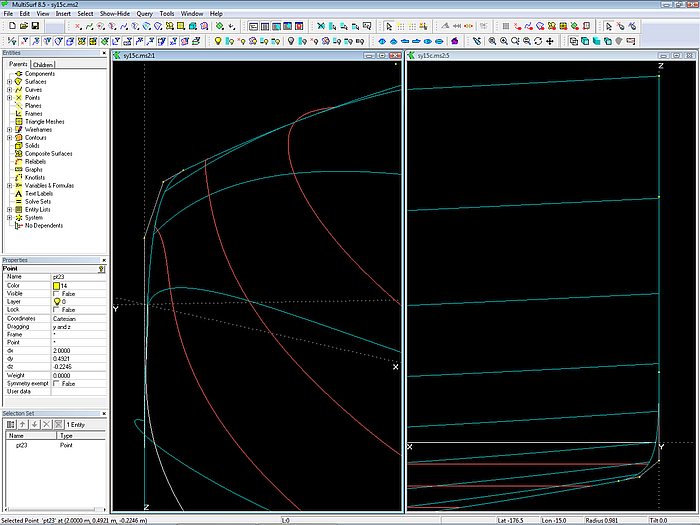
Der Strak von Kurven und Schnitten (hier Wasserlinien in rot) kann in der 3D-Ansicht auf effektive Weise überprüft werden.
Was ist der Grund für hohle Wasserlinien? Wie jeder andere Rumpfschnitt ist die Form der Wasserlinien das Resultat aus dem Verlauf der u-Parameterkurven der Rumpffläche. Wenn sie zum Steven hin beträchtlich ansteigen, treten hohle Wasserlinien auf. Ein Rumpf mit engem Vorfuß ist dafür besonders anfällig.
Wenn Wasserlinien nicht absichtlich hohl verlaufen sollen, muß der Anstieg der u-Parameterkurven hin zum Steven vermindert werden.
Hohle Waserlinien beseitigt durch Re-Verteilung der unteren Cps der Bug-Mc.
Dazu verschiebt man die unteren Cps der Bug-Mc etwas nach hinten. So steigen die u-Parameterkurven weniger steil an und die Wasserlinien werden gerade.
Warum Entity Lists?
Im Modell sy15.ms2 sind 3 Entity Lists enthalten: edit_hull_0, view_boat_0, view_lines_0. Eine Entity List enthält eine Liste von Objektnamen.
Entity Lists sind außerordentlich hilfreich bei der Kontrolle, was am Bildschirm angezeigt wird. Ein ganzer Satz von Objekten kann damit schnell ausgewählt, angezeigt oder verborgen werden. Anders als bei Layern kann ein Objekt in verschiedenen Listen enthalten sein.
Um zum Beispiel den Inhalt einer Entity List anzuzeigen: im Entities-Manager die gewünschte Liste auswählen, dann Hauptmenü/ Show Hide/ Show/ Parents (oder Toolbar-Button "Show Parents").
In der Entity List „edit_hull_0“ sind nur solche Punkte, Kurven etc. enthalten, die mit dem Modellieren der Rumpffläche zu tun haben.
Warum hull_0, stations_0 ...?
Namen sind in MultiSurf sehr wichtig. Weiß man, wie ein nicht angezeigtes Objekt heißt, kann man schneller darauf zugreifen, z. B. über „Select by Name“ oder direkte Auswahl im Entities-Manager, als über die Anzeige seine Eltern oder Kinder auf dem Bildschirm.
Darum sind einprägsame und informative Namen nützlich. Jeder wird dafür sein eigenes System entwickeln.
Der Anhang "_0" im Namen „hull_0“ bedeutet, daß es sich um die Basisfläche des Rumpfes handelt, nämlich die Fläche, die direkt von den Mcs abhängig ist. Gibt es eine von dieser Basisfläche abhängige Trimmed Surface oder SubSurface, z. B. gestutzt am Spiegel oder an der Bugrundung, heißt sie dann „hull“. „Hull_0“ signalisiert Basisfläche, „hull“ signalisiert fertige Fläche.
Somit sind „stations_0“ Spantschnitte durch die Fläche hull_0 und so weiter.
So viel zum Modell sy15.ms2. Das Modellieren eines Rundspantrumpfes mit einem durchlaufendem oder auslaufendem Längsknick wird in nachfolgenden Artikeln behandelt.