Auslaufende Spritzkante
Formmerkmale von Rümpfen
von Reinhard Siegel
Einleitung
Manche Bootsrümpfe weisen eine auslaufende Spritzkante auf. Diese Eigenschaft der Form ist eng verwandt mit einem Längsknick, der sich über einen Teil des Rumpfes erstreckt. Es gibt nicht nur eine Richtungsunstetigkeit im Spantverlauf, sondern einen ausgeprägten Absatz in den Spanten. Außerhalb des Bereichs der Spritzkante ist der Rumpf glatt und strakend.
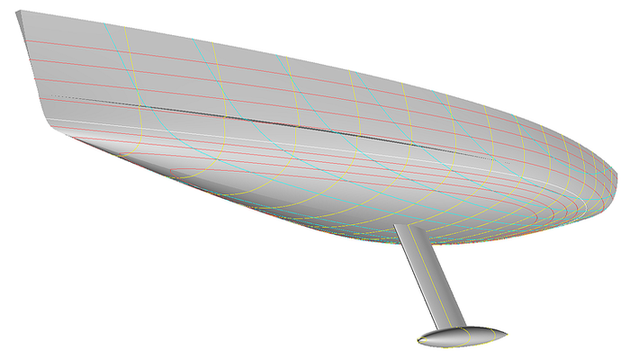
Es geht in diesem Artikel nicht um einen Rumpf mit spezifischen Abmessungen, sondern es sollen in der Praxis erprobte Vorgehensweisen gezeigt werden, um auslaufende Spritzkanten zu modellieren.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point)
Mc: Masterkurve, Stützkurve (master curve, support curve)
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
Eine auslaufende Spritzkante kann auf zwei Arten modelliert werden:
1 - der Rumpf wird aus zwei Basisflächen zusammengesetzt, die sich bis auf den Bereich der Spritzkante entlang einer gemeinsamen Längskante ohne Knick berühren.
2 - eine fertige Rumpffläche wird in zwei Längsstreifen aufgeteilt und im Bereich der Spritzkante wird der obere Streifen nach außen gedrückt.
Methode 1
In Modell cloft-cloft-spraychine.ms2 setzt sich der Rumpf aus zwei separaten Flächen zusammen, eine Fläche für die Seite und eine Fläche für den Boden. Beides sind C-spline Lofted Surfaces und nach der Vertexkurven-Methode aufgebaut (siehe hierzu auch den Artikel „Modellieren von Rundspantrümpfen“). Die Anzahl der B-spline-Masterkurven (Mc), ihre Längsposition sowie die Anzahl ihrer Kontrollpunkte (Cp) ist jeweils gleich. C-spline Curves verlaufen als Strakhilfe durch korrespondierende Kontrollpunkte (Vertexkurven).
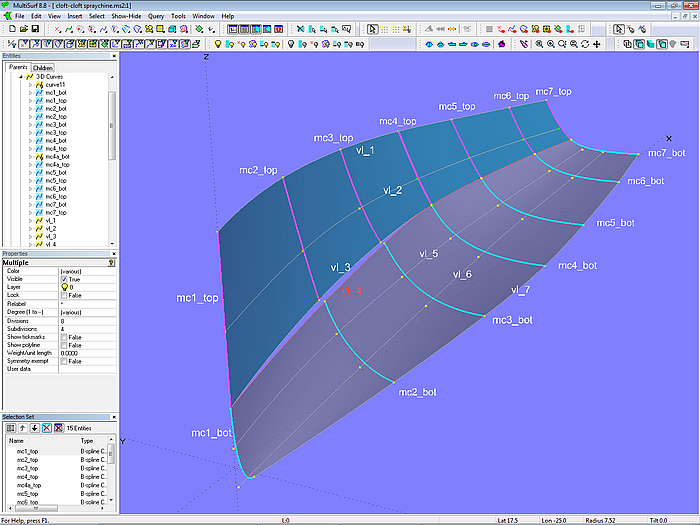
Modell cloft-cloft-spraychine.ms2 – Anordnung der Masterkurven und der Hilfskurven für den Strak der beiden C-spline Lofted Surfaces Seite und Boden
Die Vertexkurve vl_3 beschreibt die Unterkante der Seitenfläche, die Vertexkurve vl_4 die Oberkante der Bodenfläche. Zwar haben vl_3 und vl_4 ab Mc4 die gleichen Kontrollpunkte, aber das ist keine Gewähr, daß beide Kurven übereinander liegen. Wie man dies erzwingen kann, ist in Modell ccurve.ms2 gezeigt.
Side step
Modell ccurve.ms2 enthält die beiden C-spline Curves c1 und c2, jeweils gestützt durch 6 Cps. Davon sind 5 gemeinsame Cps, sowie die beiden unterschiedlichen Punkte p2_a und p2_b. Zwar verlaufen die Kurven durch die gemeinsamen Cps, liegen aber ab dem Stützpunkt p3 nicht genau übereinander. Die Abweichung nimmt allmählich ab, verschwindet aber nicht ganz.
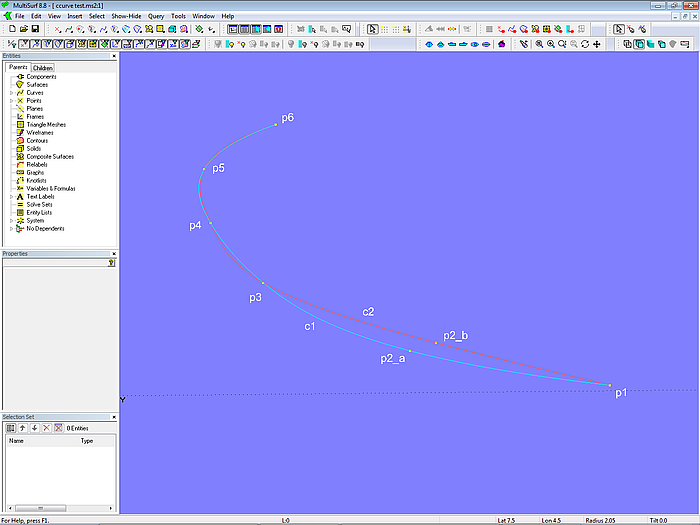
Modell ccurve.ms2 –abweichender Verlauf zweier C-spline Curves trotz gemeinsamer Kontrollpunkte
Setzt man jetzt auf die Kurve c1 einen Bead e1 kurz hinter p3 und nimmt e1 als weiteren Cp zur Kurve c2 hinzu, dann verläuft c2 gleich wie c1. Dies ist analog zum manuellen Zeichnen mit einer Straklatte, die man in eine bestimmte Richtung zwingen kann, in dem zwei Gewichte dicht nebeneinander stellt.
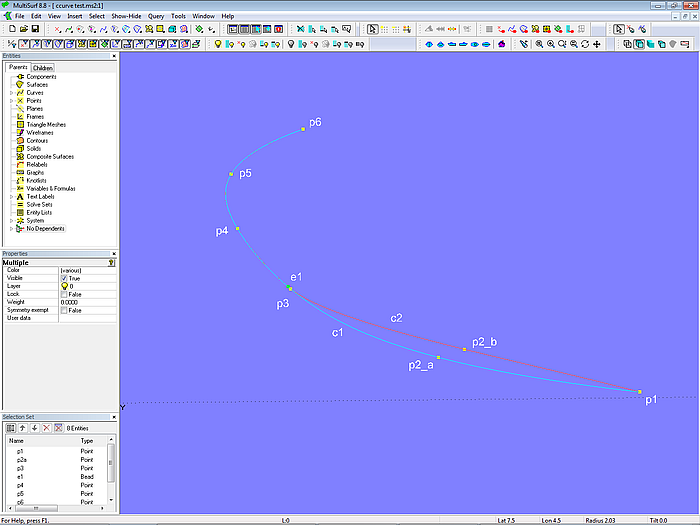
Modell ccurve.ms2 –gemeinsamer Kurvenverlauf, erzwungen durch zwei Kontrollpunkte in engem Abstand
Die Kurve c2 ist nun durch 7 Cps gestützt, wobei e1 als Bead auf c1 ein passiver Kontrollpunkt für c2 ist, da er nicht frei ist, sondern nur auf der Kurve c1 verschoben werden kann.
Zurück zu Modell cloft-cloft-spraychine.ms2.
Auch hier ist kurz hinter dem ersten gemeinsamen Cp am Ende der Spritzkante ein Bead e1 auf die Vertexkurve vl_3 gesetzt, der nun als zusätzlicher Cp für vl_4 dient, um das Zusammenlaufen zu erzwingen. Wird jetzt für die Fläche Boden dicht hinter Mc4 eine weitere Masterkurve (mc4a_bot) eingesetzt und e1 als ersten Punkt für diese Kurve verwendet, ist sichergestellt, daß die Ränder von Seitenfläche und Bodenfläche zusammenfallen.
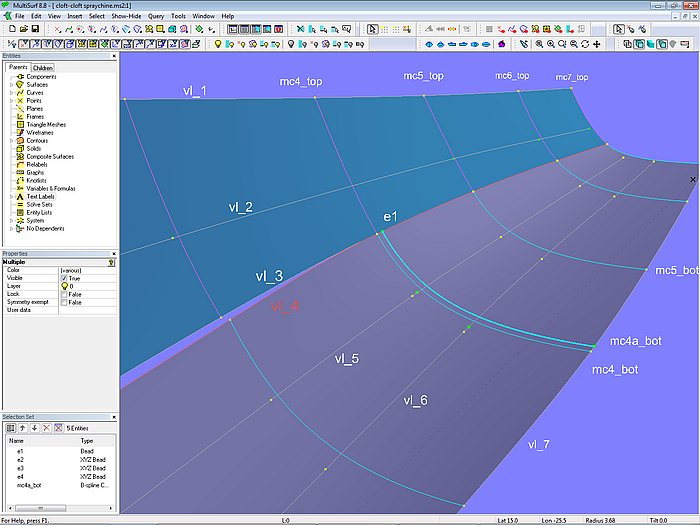
Modell cloft-cloft-spraychine.ms2 – in engem Abstand zusätzlich angeordnete Masterkurve mc4a_bot erzwingt das Zusammenlaufen von Seite und Boden und damit das Auslaufen der Spritzkante.
Die anderen Cps von mc4a_bot erhalten wir als Schnittpunkte (XYZBeads) mit den Vertexkurven vl_5, vl_6 und vl_7 an der Längsposition von e1.
Durch diese Konstruktion, die nur passive Cps für die in engem Abstand zusätzlich angeordnete Masterkurve verwendet, wird das Zusammenlaufen beider Flächen in Längsrichtung festverdrahtet.
Aber wie wird gewährleistet, daß ab Mc4, wo die Spritzkante ausläuft, kein Knick in Querrichtung zwischen Seite und Boden entsteht?
Damit keine solche Unstetigkeit entsteht, müssen die Mcs des Bodens mit der gleichen Richtung beginnen, mit der die Mcs der Seite enden. Das ist dann der Fall, wenn der vorletzte Cp der oberen Mc, der gemeinsame Cp sowie der zweite Cp der unteren Mc auf einer Linie liegen. B-spline Curves beginnen immer tangential zum ersten Segment und enden immer tangential zum letzten Segment des Polygonzugs durch ihre Kontrollpunkte.
Um diese Beziehung fest einzubauen, wird im Modell cloft-cloft-spraychine.ms2 eine Line zwischen dem vorletzten und letzten Cp der oberen Mc aufgespannt. Und darauf ein Bead gesetzt, der als zweiter Cp für die untere Mc verwendet wird.
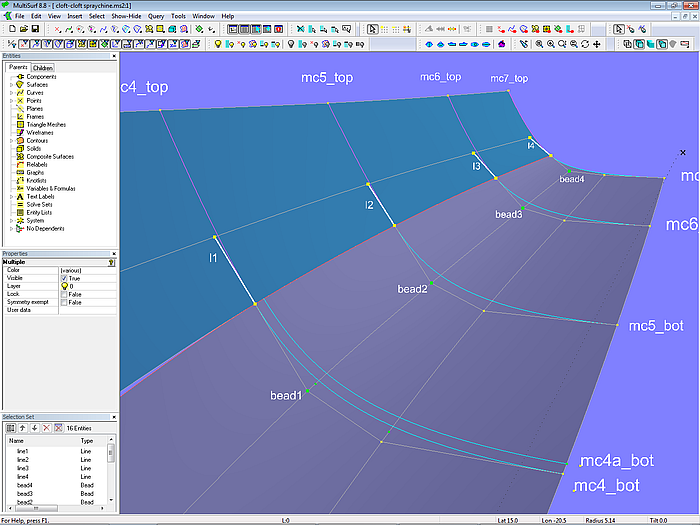
Modell cloft-cloft-spraychine.ms2 – tangentialer Übergang zwischen den Mcs von Seite und Boden durch Anordnung der benachbarten Cps auf einer Linie
Damit ist der knickfreie Übergang der Seite in den Boden festverdrahtet.
Die eigentliche Spritzkantenfläche ist eine Ruled Surface, aufgespannt zwischen SubSnakes auf den jeweiligen EdgeSnakes von Seite und Boden.
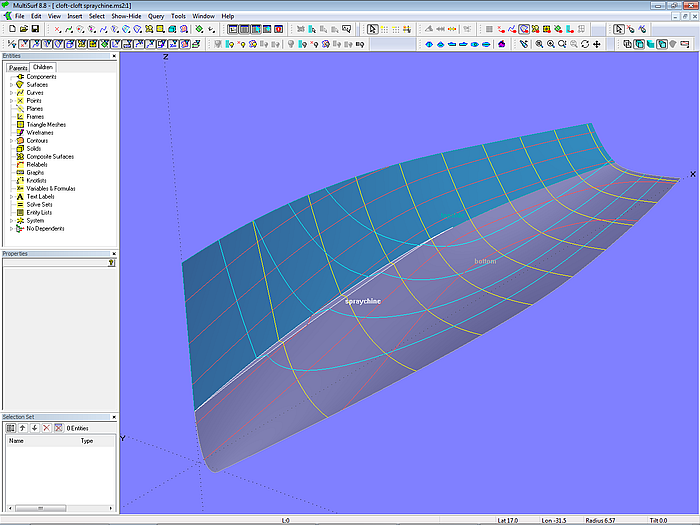
Modell cloft-cloft-spraychine.ms2 – Ruled Surface spraychine aufgespannt zwischen den offenen Kanten von Seite und Boden
Methode 2a
Man kann sich eine auslaufende Spritzkante auch so entstanden denken, daß eine fertige Rumpffläche entlang einer Längskurve in eine Fläche Seite und eine Fläche Boden aufgeteilt wird und dann die Seite im Bereich der Spritzkante nach außen gedrückt wird.
Modell cloft-spraychine.ms2 zeigt diesen Ansatz. Die Rumpffläche ist eine C-spline Lofted Surface mit 6 B-spline-Mcs zu je 6 Cps. Durch die Cps verlaufen C-spline Curves als Strakhilfskurven (Vertexkurven).
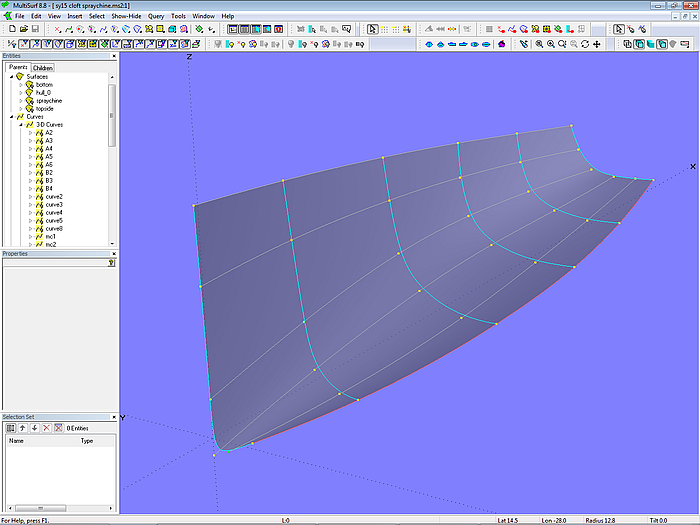
Modell cloft-spraychine – Anordnung von Masterkurven und Vertexkurven der C-spline Lofted Surface
Kurz hinter Mc3 (deren erster Kontrollpunkt p31 ist) wird auf der Vertexkurve vl_1 der Bead e1 erzeugt. Dann werden an dieser Position die anderen Vertexkurven geschnitten (XYZBeads). Nun wird mit diesen passiven Kontrollpunkten eine weitere Masterkurve bestimmt. Es ist der Zweck dieser Masterkurve, die Rumpfläche am Ende der Spritzkante festzuklammern.
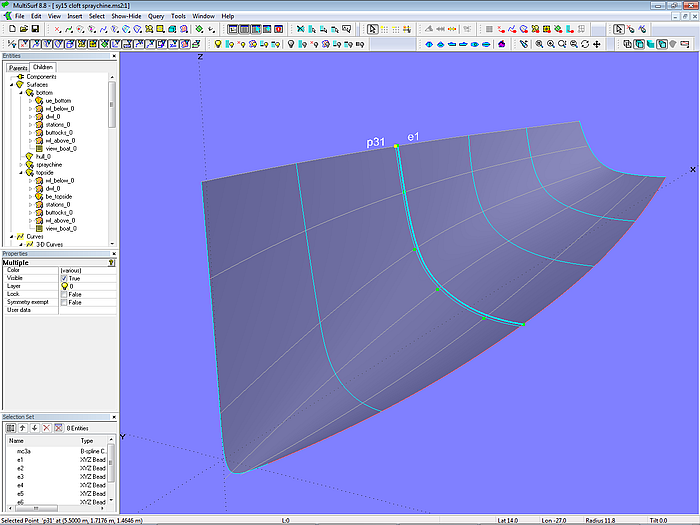
Modell cloft-spraychine.ms2 – in engem Abstand zusätzlich angeordnete Masterkurve
Anschließend wird auf jede Mc ein Bead gesetzt und durch diese in Längsrichtung eine C-spline Curve gelegt, die den Verlauf der Spritzkante beschreibt.
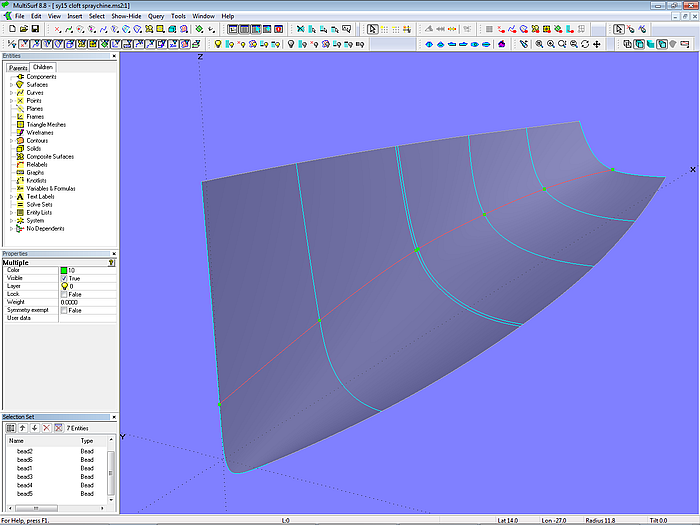
Modell cloft-spraychine.ms2 – Verlauf der Spritzkante (C-spline Curve durch Beads auf den Masterkurven)
Jede Mc wird nun mit Hilfe des Beads in zwei SubCurves aufgeteilt. Alle unteren SubCurves sind Mcs für den Boden.
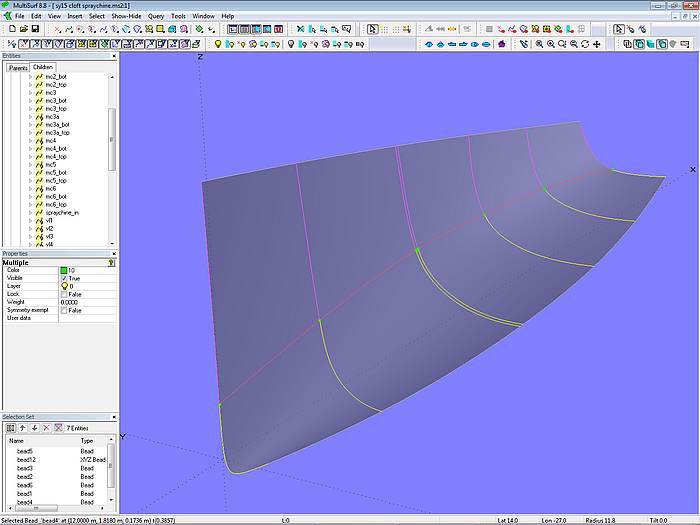
Modell cloft-spraychine.ms2 – Aufteilung der Masterkurven in SubCurves für Boden und Seite
Anschließend wird die zweite Mc der Seite durch eine Relative Curve (mc2a_new) ersetzt, so daß ein Spalt entsteht. Mit dieser und den anderen oberen SubCurves als Mcs wird die Seitenfläche definiert.
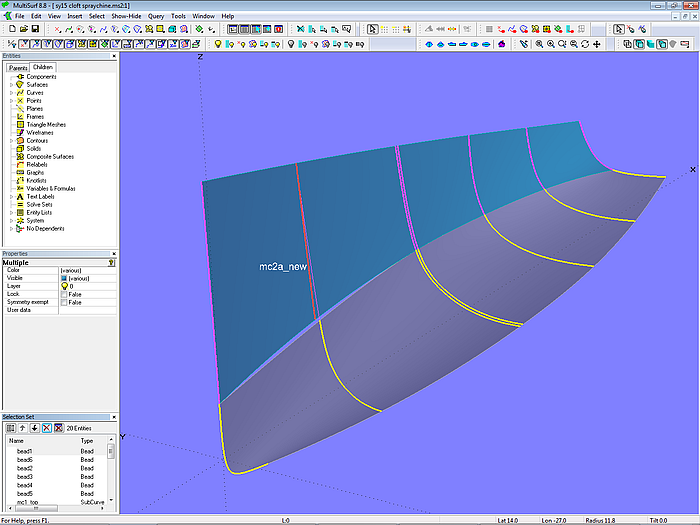
Modell cloft-spraychine.ms2 – Masterkurven für Seite und Boden. Die Relative Curve mc2a_new bestimmt die Breite der auslaufenden Spritzkante.
Wie im vorherigen Modell ist die Fläche der Spritzkante eine Ruled Surface, aufgespannt zwischen SubSnakes auf den jeweiligen EdgeSnakes von Seite und Boden.
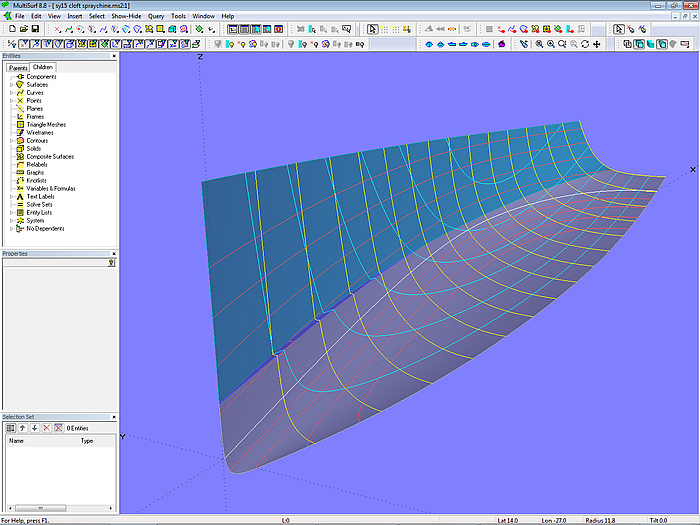
Modell cloft-spraychine.ms2 – Seite und Boden sind C-spline Lofted Surfaces, die auslaufende Spritzkante ist eine Ruled Surface.
Anders als im vorherigen Modell ist keine Hilfskonstruktion erforderlich, damit sich die Masterkurven für Seite und Boden tangential berühren, sondern es werden die von Oberkante bis Bodenkontur durchlaufenden Mcs geteilt. In beiden Modellen sorgt eine in engem Abstand angeordnete zusätzliche Masterkurve für den gleichen Verlauf von Seite und Boden entlang ihres gemeinsamen Rands.
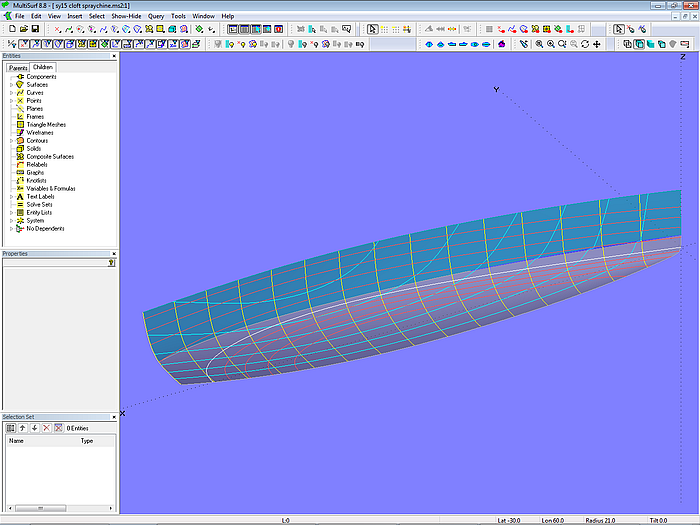
Modell cloft-spraychine.ms2
Methode 2b
Modell blister-spraychine.ms2 zeigt einen anderen Ansatz. Ausgangspunkt ist ebenfalls eine fertige Rumpffläche.
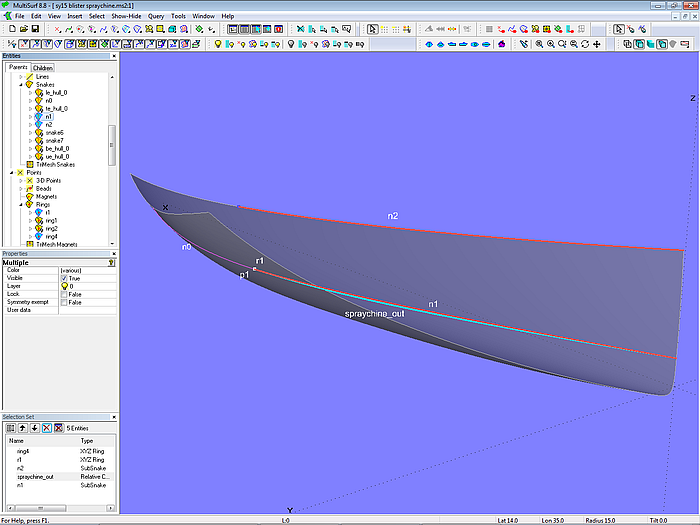
Modell blister-spraychine.ms2 – Subsnake n1 und Relative Curve spraychine_out bestimmen die Ränder der auslaufenden Spritzkante.
Die Snake n0 teilt die Rumpffläche in zwei Bereiche und bestimmt so den Verlauf der Spritzkante. Auf der Snake n0 liegt der Ring r1, der das Ende der Spritzkante festlegt. Die SubSnake n1 ist das vordere Teilstück von n0. Den Verlauf der Außenkante der Spritzkante definiert die Relative Curve spraychine_out. Die Breite der Spritzkante wird bestimmt durch den Punkt p1, der relativ zum Ring r1 liegt.
Desweiteren liegt auf der Rumpfoberkante (EdgeSnake) die SubSnake n2.
Mit den beiden Snakes n2 und n1 und der Relative Curve spraychine_out wird nun eine Blister-Fläche erzeugt. Der Flächenbereich zwischen den beiden Snakes wird quasi „aufgeweicht“ und die Kante n1 nach außen „geklappt“, bis sie mit der Kurve spraychine_out übereinstimmt.
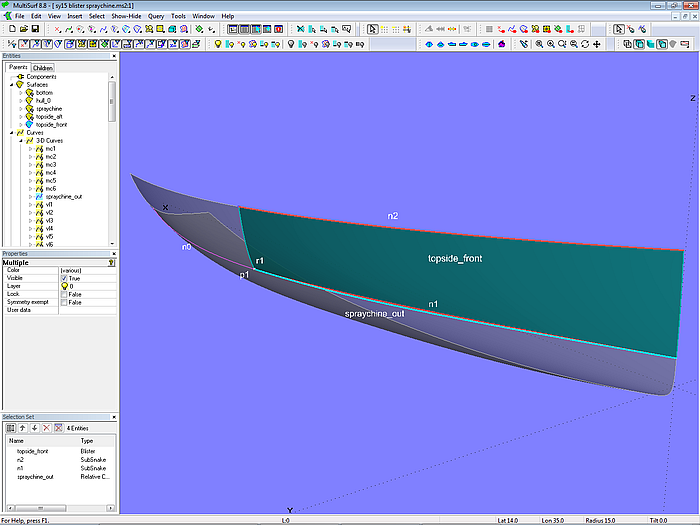
Modell blister-spraychine.ms2 – Blister-Fläche topside_front
Entscheidend für den Verlauf der Relative Curve spraychine_out ist die Verwendung eines Graphs. Damit läßt sich die Verteilung der Distanz zwischen den Punkten r1 und p1 über der Länge der Relative Curve kontrollieren.

Modell blister-spraychine.ms2 – der Verlauf der Relative Curve spraychine_out wird durch einen Graph kontrolliert. Dadurch läßt sich auch der tangentiale Einlauf in das Ende der SubSnake n1 auf einfache Weise vorgeben.
Der Verlauf eines Graphs kann über View/ Display/ Profile/ Graph dargestellt werden. Im Profile-Fenster können die Werte des Graphs auch mit den Pfeil-Tasten oder per Maus verändert werden..
Im vorliegenden Beispiel sind die beiden letzten Werte des Graphs gleich Null, so daß die Relative Curve tangential in das Ende der SubSnake n1 einläuft.
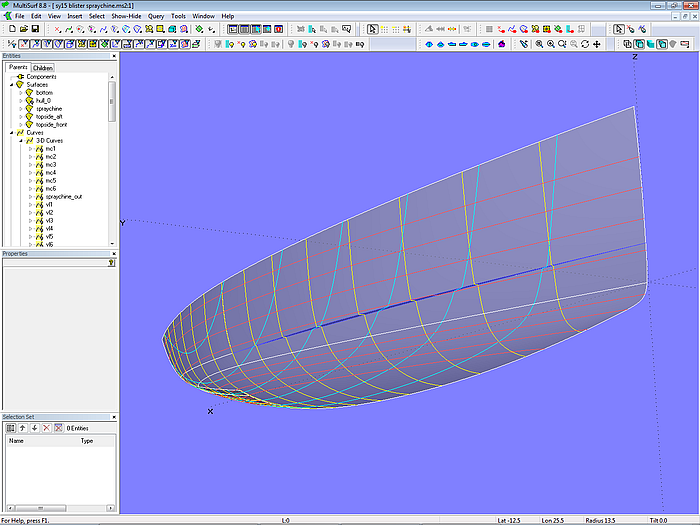
Modell blister-spraychine.ms2