Decks und Aufbauten
von Reinhard Siegel
Einleitung
Kleine Boote kommen ohne Deck und Aufbau aus, aber bei größeren Booten sind sie unverzichtbare Bestandteile des Wasserfahrzeugs. Dieser Artikel beschreibt verschiedene Methoden, in MultiSurf Flächen für Decks und Aufbauten zu modellieren.
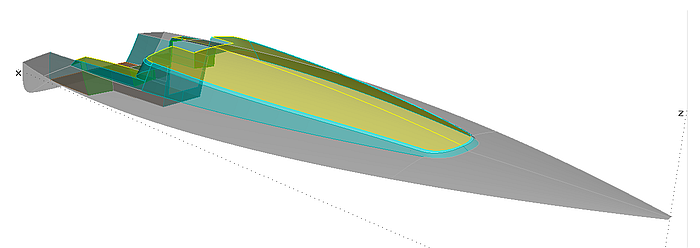
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point)
Mc: Masterkurve, Stützkurve (master curve, support curve)
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
1 - Decks
Bevor wir einen Aufbau modellieren können, benötigen wir ein Deck. Oft ist ein Deck wenig mehr als ein Vor- und Seitendeck. Dennoch ist es sinnvoll, mit einer Basisfläche von Bug bis Heck zu beginnen und anschließend den von Aufbau und Cockpit überdeckten Bereich herauszuschneiden. Dann läßt sich leicht Bucht oder Sprung des Decks ändern, ohne daß man auf den Strak und das Aneinanderhängen von Einzelflächen achten muß.
Methode 1: Freiformen
Wie ein Bootsrumpf läßt sich auch ein Deck nach der Methode „Masterkurven beplanken“ modellieren. Diese Methode bietet die größte Flexibilität in Bezug auf Verlauf der Höhe der Decksbucht in Längsrichtung und Formgebung in Querrichtung.
Es bietet sich an, für das Deck den gleichen Flächentyp wie für den Rumpf zu verwenden und die Deckbalken-Masterkurven an die gleiche Position wie die Masterkurven für die Rumpffläche zu setzen. Dann schließen beide Flächen entlang der gemeinsamen Kante wasserdicht aneinander.
C-spline Lofted Surface über B-spline Mcs
Modell deck_cloft_bcurve.ms2 zeigt ein Deck mit B-spline Curves als Deckbalken-Masterkurven. Jede Mc wird mit 3 Cps definiert, wobei cp1 der erste Punkt der Rumpfmasterkurve ist. Damit die Deck-Mc senkrecht zur Mittschiffsebene endet, wird cp2 auf diese projeziert als Projected Point cp3.
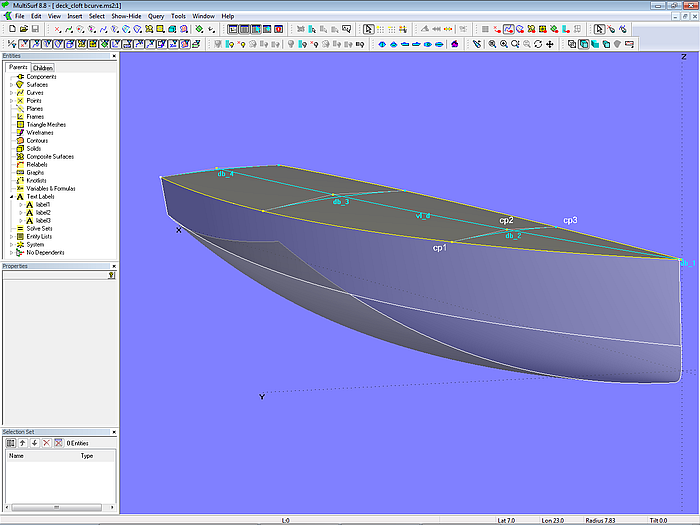
Modell deck_cloft_bcurve.ms2 - Deck als C-spline Lofted Surface mit 4 B-spline-Masterkurven
Als Strakhilfe für den harmonischen Verlauf der Balkenbuchthöhe über der Länge verläuft die Vertexkurve vl_d durch alle Punkte cp2 der Mcs. Sieht man in der 3D-Ansicht schleifend entlang dieser Kurve, lassen sich Unregelmäßigkeiten leicht erkennen.
Je weiter cp2 nach außen zur Deckskante hin positioniert wird, umso parabelförmiger wird die Deckbalken-Mc.
Natürlich können mehr als 3 Cps für die Masterkurven verwendet werden, aber der Schlüssel zum Strak ist Einfachheit.
C-spline Lofted Surface mit Arc-Mcs
Alternativ kann man für die Mcs auch Kreisbögen verwenden. Dies zeigt Modell deck_cloft_arc.ms2.
Nur die Höhe von cp2 über cp1 am Rand des Rumpfes spielt hier eine Rolle, nicht seine Y-Position. Der Type 5 des Arc stellt sicher, daß der Bogen senkrecht zur Mittschiffsebene endet.
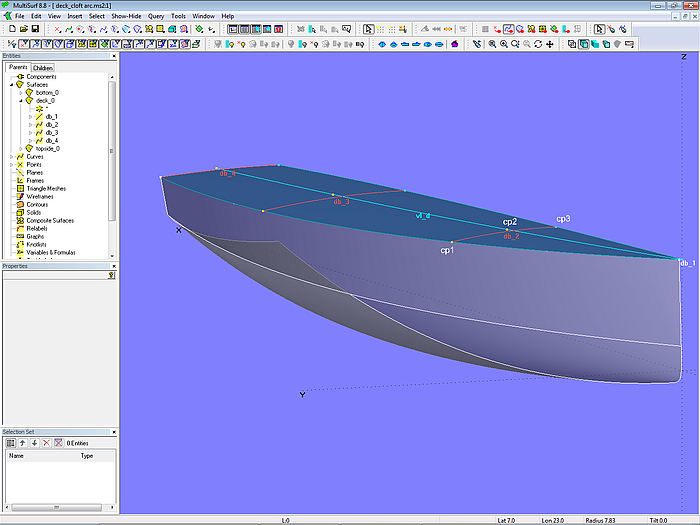
Modell deck_cloft_arc.ms2 – Deck als C-spline Lofted Surface mit 4 Kreisbogen-Masterkurven
Arc Lofted Surface mit längslaufenden Mcs
Bislang wurde ähnlich zur Rumpffläche das Deck von querlaufenden Mcs gestützt. In Modell deck_arcloft.ms2 dagegen spannen die längslaufenden Mcs vl_1, vl_d und c0 eine Arc Lofted Surface auf. Die Kurve vl_d, die vom gleichen Typ wie die Vertexkurve vl_1 ist, bestimmt die Buchthöhe; ihre Cps liegen genau vertikal über dem 1. Cp der Rumpf-Mcs. Damit die Arc Lofted Surface vom Typ 5 senkrecht zur Mittschiffsebene endet, wird vl_d als c0 auf diese projeziert.
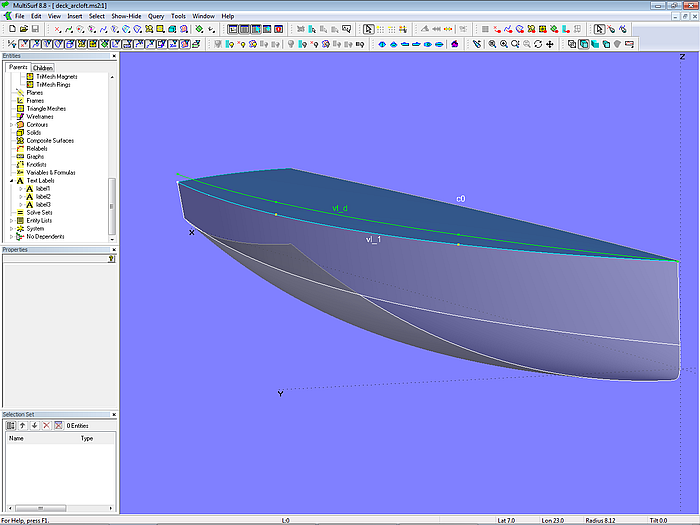
Modell deck_arcloft.ms2 – Deck als Arc Lofted Surface mit längslaufenden Mcs; c0 ist die Projektion von vl_d auf die Mittschiffsebene.
Alternativ könnte vl_d auch eine Relative Curve zur Vertexkurve vl_1 sein, deren Verlauf durch einen BGraph gesteuert wird.
Methode 2: prozedurale Konstruktion
Decksbalken gleicher Form
Mitunter ist es von Vorteil, wenn alle Balken eines Decks die gleiche Form haben, also Abschnitte eines einzigen Malls sind. Zum Beispiel wenn Holzdeckbalken lamelliert werden.
Modell deck_const_pattern.ms2 zeigt diesen Ansatz. Das Balkenbuchtmall ist die Kurve pattern, die über dem Vorsteven als Arc definiert ist. Die Oberkante des Rumpfes ist die EdgeSnake n0. Auf dieser liegt der Ring d_sheer. Nun wird die Kurve pattern geschnitten im Intersection Bead d_e0, wobei die Schnittebene parallel zu Mitte Schiff ist und durch d_sheer geht. Der Kurvenabschnitt von MS bis d_e0 (SubCurve sub_pattern) wird abschließend an die Position von d_sheer kopiert (Copy Curve moving_cv). Die Procedural Surface deck_0 wiederholt diese Konstruktion für alle Positionen von d_sheer.
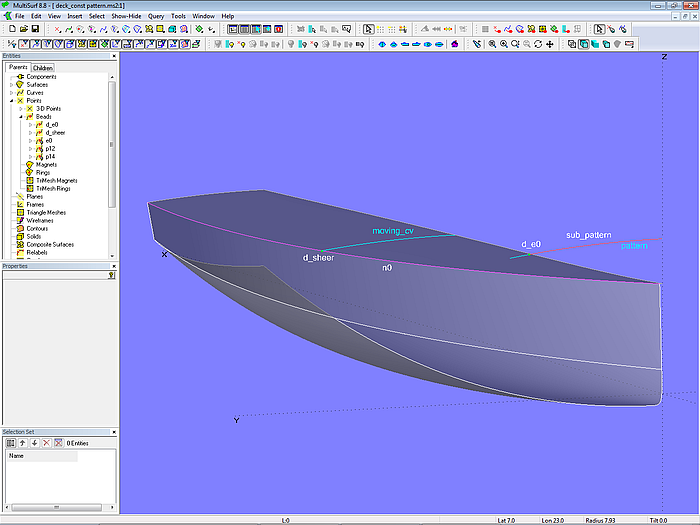
Modell deck_const_pattern.ms2 - Deck mit gleichen Decksbalken als Procedural Surface
Da der Ring d_sheer auf der Edgesnake n0 liegt, hat das Deck das gleiche Labeling wie die Rumpffläche; das garantiert eine wasserdichte Verbindung beider Flächen entlang der gemeinsamen Kante.
Deck mit gleichem Buchtverhältnis
Ebenfalls mit einer prozeduralen Konstruktion läßt sich eine Decksfläche erzeugen, bei der die Buchthöhe in einem konstanten Verhältnis zur Decksbreite steht. Modell deck_constant_camber_ratio.ms2 zeigt diese Variante.
Angetrieben wird die Konstruktion wiederum von dem Ring d_sheer, der auf der Rumpfoberkante liegt (EdgeSnake n0). Dieser Ring wird auf die Mittschiffsebene (Y=0) projeziert im Projected Point d0. Die Line half_chord zwischen d_sheer und d0 ist die halbe Breite an der Position von d_sheer. Nun wird auf dieser Line der Bead ratio gesetzt, dessen t-Parameterwert der Hälfte des Buchtverhältnisses ist. Soll das Verhältnis Buchthöhe zu Breite zum Beispiel 15% betragen, ist der t-Wert für ratio auf 0.075 zu setzen. (Die Position eines Beads auf einer Line entspricht dem Wert seines Parameters t; für t = 0.33 liegt der Bead auf 1/3 der Länge, für t = 0.5 auf der Hälfte usw.)
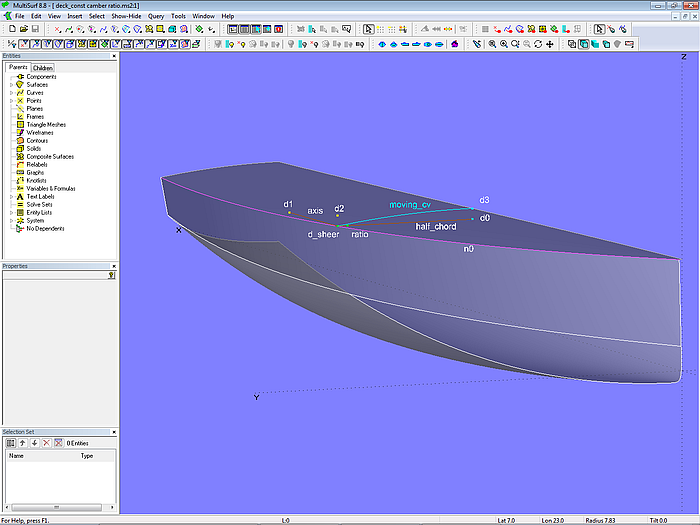
Modell deck_constant_camber_ration.ms2 – Deck mit konstantem Buchtverhältnis als Procedural Surface
Dieser Bead ratio wird nun um 90 Grad nach oben gedreht (Rotated Point d2) und dieser dann auf MS projeziert im Projected Point d3. Abschließend wird mit den Punkten d_sheer, d2 und d3 der Arc moving_cv definiert. Die Procedural Surface deck_0 wiederholt nun für alle Positionen von d_sheer auf n0 diese Decksbalkenkonstruktion.
Methode 3: abwickelbares Deck
Ein Deck läßt sich auch als abwickelbare Fläche erzeugen. Dies wird in Modell deck_devsurf.ms2 gezeigt. Die Developable Surface deck_0 wird aufgespannt zwischen der Oberkante des Rumpfes (EdgeSnake n0) und einem Decksbalken am Heck (Arc db).
Der Preis für die einfachere Fertigung einer abwickelbaren Fläche (nur Verbiegung) ist die Einschränkung in der Form. Die Deckskurve auf MS ist gerade, Spanten durch das Deck verlaufen teilweise auch gerade.
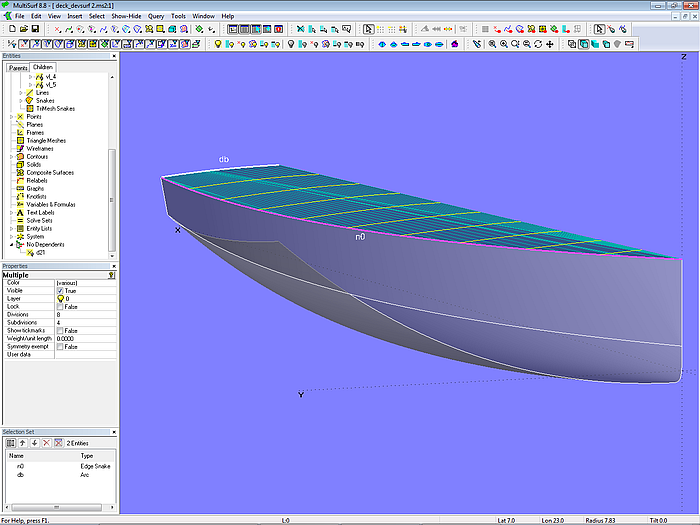
Modell deck_devsurf.ms2 – abwickelbare Fläche aufgespannt zwischen Oberkante Rumpf n0 und Deckbalken db achtern
So viel zu möglichen Deckkonstruktionen.
2 – Der kastenförmige Aufbau
Aufbau 1 - Freiformen
Die einfachste Form eines Aufbaus ist der Kasten. Er besteht aus Seitenwand, Frontwand, Rückwand und Dach. Das Modell trunk_cabin-1.ms2 zeigt ein Beispiel.
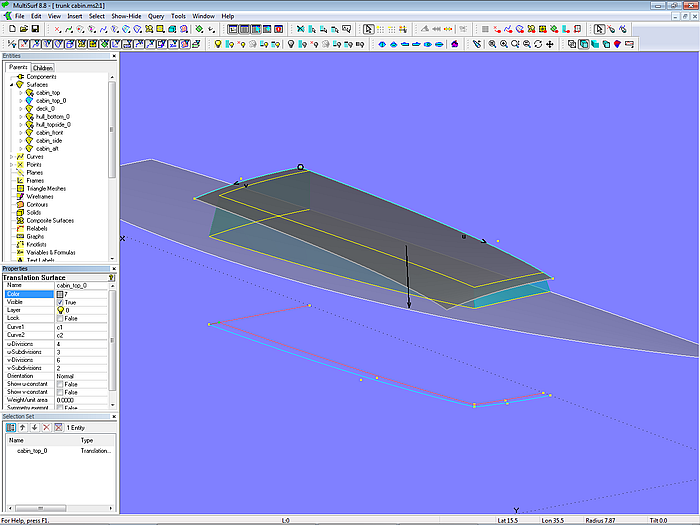
Modell trunk_cabin.ms2 – Aufbau in Kastenform
Die Basisfläche des Aufbaudachs ist eine Translation Surface; Leitkurve ist eine B-spline Curve auf Mitte Schiff, erzeugende Kurve ein Kreisbogen. Auf diese Basisfläche werden die Unter- und Oberkanten der Aufbauwände projeziert (als Projected Snakes), die In der XY-Ebene definiert sind. Dadurch bleibt in der Aufsicht die Aufbauform gleich, wenn man das Deck ändert.
Hinweis: es ist wichtig, daß das Deck strakt. Denn eine Projected Snake, die eine glatte Kurve auf ein nicht strakendes Deck abbildet, ist nicht glatt. Eine von der Snake abhängige Fläche strakt nicht. Eine Fläche, die von einer Snake auf einem nicht strakendem Deck abhängt, strakt nicht.
Alle Deckbalken des Dachs sind gleich. Alle Wände sind abwickelbar, das Dach aber nicht. Es wäre nur dann abwickelbar, wenn das Dach auf Mitte Schiff eine Line wäre.
Nur die Dachfläche ist größer als ihre fertige Form, alle anderen Flächen müssen nicht getrimmt werden.
Man kann bei dieser Konstruktion nur die Kurven für die Flächenkanten ändern und dann sehen, ob es einem gefällt. Spezielle Vorgaben wie z. B. Einfall der Seitenwand oder Neigung der Front, sind nicht möglich.
Aufbau 2 - Vorgaben
Gibt es geometrische Vorgaben, wie zum Beispiel: Einfall der Seitenwand 10°, Front mit Kreisbucht und Neigung 35°, ist ein Vorgehen wie in Modell trunk_cabin-2.ms2 möglich.
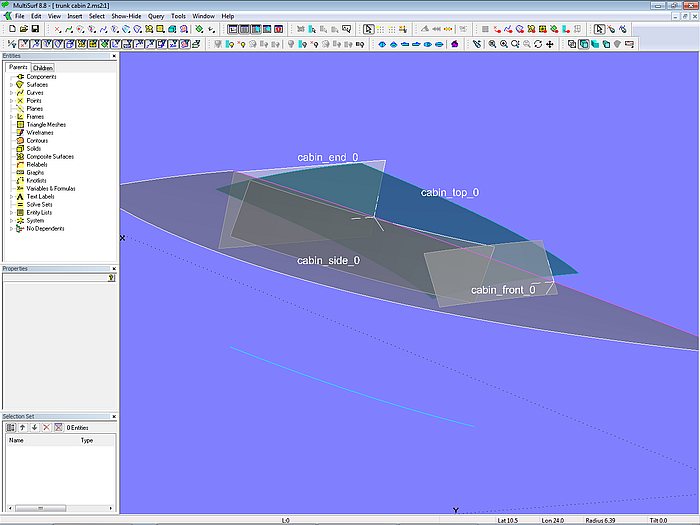
Modell trunk_cabin-2.ms2 – Basisflächen für Aufbaudach, –seite, - front, und -ende
Zunächst werden die Aufbauflächen als etwas größere Flächen erstellt, die jeweils für sich die geforderte Form haben.
Beginnen wir mit dem Aufbaudach. Gefordert sind Deckenbalken, die über einem Mall lamelliert werden sollen. Daher wird eine Translation Surface verwendet. Leitkurve ist B-spline Curve c1 auf MS, erzeugende Kurve ist Arc c2 (Kreisbogen). Über die Eigenschaft „Dragging“ sind ihre Kontrollpunkte so festgelegt, das stets c1 auf MS bleibt und c2 senkrecht zu MS verläuft.
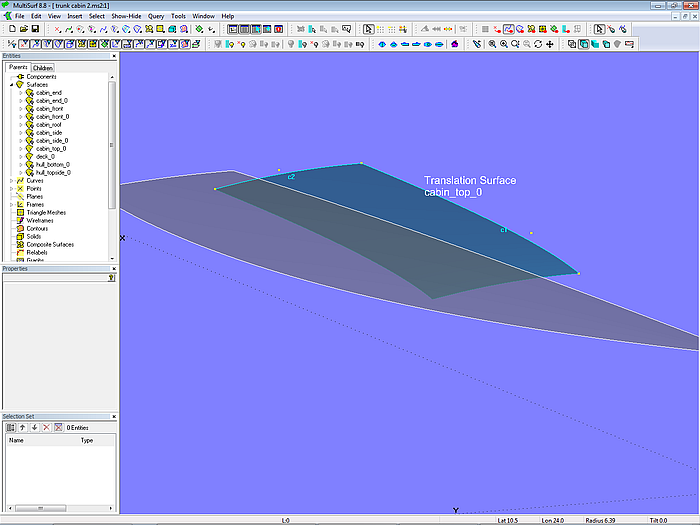
Modell trunk_cabin-2.ms2 – Konstruktion der Grundfläche für das Aufbaudach
Die Front soll in Position und Neigung veränderbar sein, die Krümmung in Querrichtung die Form eines Kreisbogens haben. Darum wird auf die Snake n0 der XYZRing ring1 gesetzt und mit den Punkten pt1 und pt3 ein 3-point Frame definiert. Auf diesen Frame beziehen sich die Punkte pt2, pt4 und pt5, die den Kreisbogen c3 bestimmen (hier ist es ein Arc, man könnte aber auch einen RadiusArc verwenden, bei dem man einen gewünschten Radiuswert angeben kann). Zwischen pt1 und pt2 ist die Line line1 aufgespannt. Mit dieser und c3 ist damit die Translation Surface cabin_front_0 definiert.
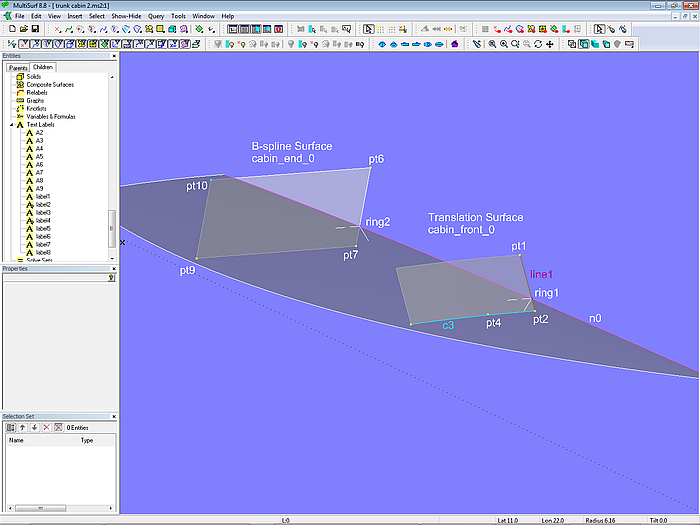
Modell trunk_cabin-2.ms2 – Konstruktion der Grundflächen für Aufbaufront und -ende
Die Aufbaurückwand soll eben sein und nur in der Neigung und Position varierbar. Mit Ring ring2, pt6 und pt8 ist der hintere 3-point Frame erzeugt, und in diesem liegen die Punkte pt7 und pt9. Pt10 ist ein Copy Point, der für die Ebenheit der rechteckigen B-spline Surface cabin_end_0 sorgt.
Hinweis: eine ebene rechteckige Fläche läßt sich am einfachsten mit 4 Punkten und einer B-spline Surface vom Typ 1 sowohl in u- wie in v-Richtung erzeugen. Drei der Punkte bestimmen die räumliche Lage der Fläche, der 4. Punkt ist ein Copy Point mit den anderen Punkten als Eltern.
Die Aufbauseite soll eine konstante Neigung nach innen haben. Sie ist ebenfalls eine Translation Surface. Auf der XY-Ebene ist der Verlauf der Unterkante als B-spline Curve c0 definiert. Diese wird dann auf das Deck als Projected Snake n1 projeziert. Am hinteren Ende von c0 liegt der Ring ring3, von dem der Punkt pt11 abhängt, der Höhe und Neigung kontrolliert. Mit der Line line2 zwischen ring3 und pt11 als Erzeugende und der Snake n1 als Leitkurve ist die Basisfläche cabin_side_0 der Aufbauseite bestimmt.
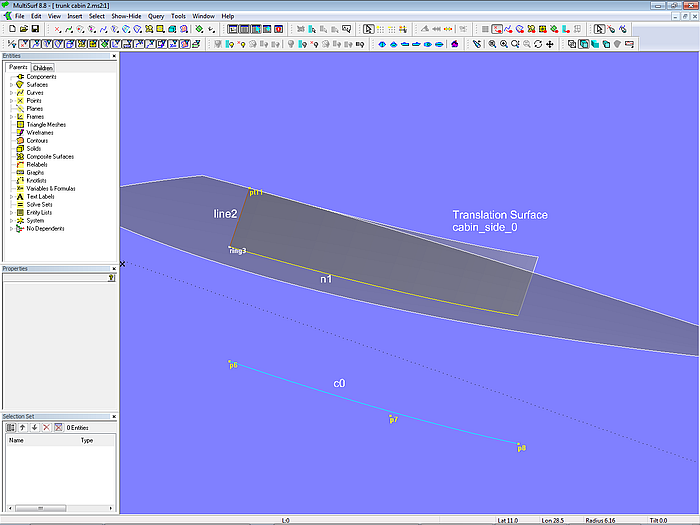
Modell trunk_cabin-2.ms2 – Konstruktion der Grundfläche für die Aufbauseite
Nachdem nun die Grundflächen erzeugt sind, müssen die überstehenden Flächenteile abgeschnitten werden. Betrachten wir zuerst die Front des Aufbaus. Sie wird vom Dach, vom Deck und von der Aufbauseite durchdrungen.
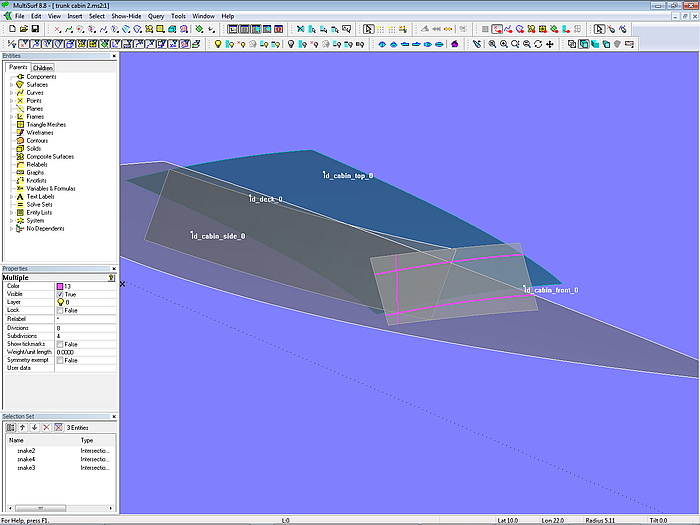
Modell trunk_cabin-2.ms2 – Durchdringung der Aufbaufront mit Deck, Aufbauseite und -dach
Diese Durchdringungen werden durch 3 Intersection Snakes bestimmt, die alle auf der Translation Surface cabin_front_0 liegen. Die nicht überstehenden Teilstücke dieser Snakes werden durch SubSnakes bestimmt, die ihrerseits als die Randkurven für die Trimmed Surface cabin_front dienen. Diese ist die fertige Frontfläche.
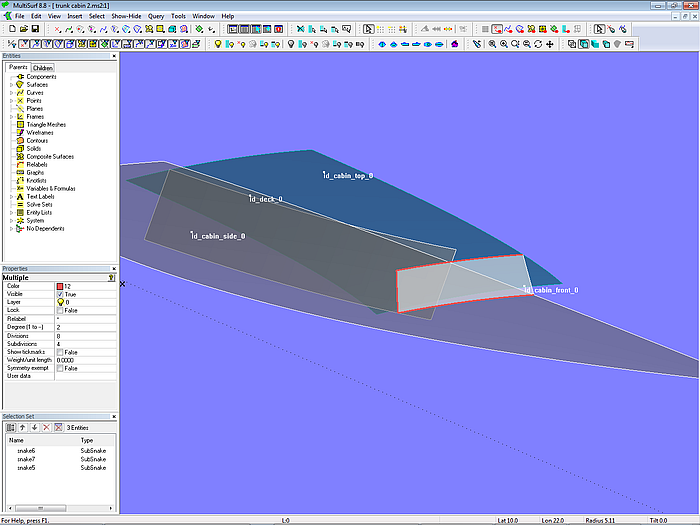
Modell trunk_cabin-2.ms2 – fertige Frontfläche als Trimmed Surface
In gleicher Weise wird mit dem anderen Flächen verfahren. Zuerst die Durchdringung mit den benachbarten Flächen bestimmen (Intersection Snakes), dann die nichtüberstehenden Kurvenstücke als SubSnakes erzeugen, und mit diesen dann die fertigen Flächen als Trimmed Surface.
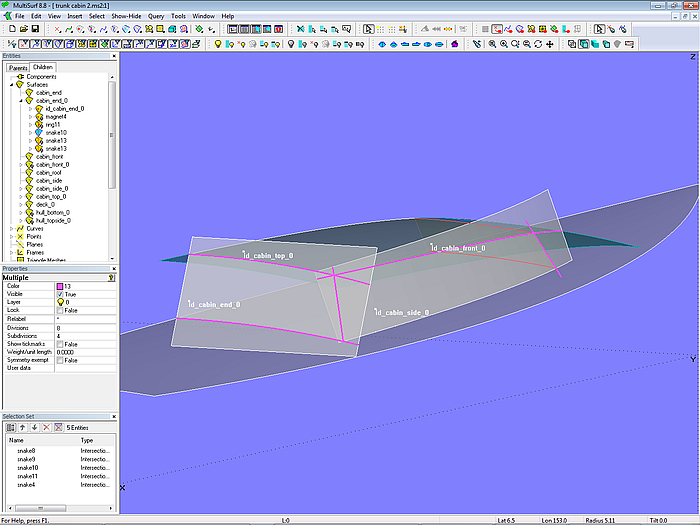
Modell trunk_cabin-2.ms2 – Durchdringung der Grundflächen von Deck, Dach, Seite und Aufbauende
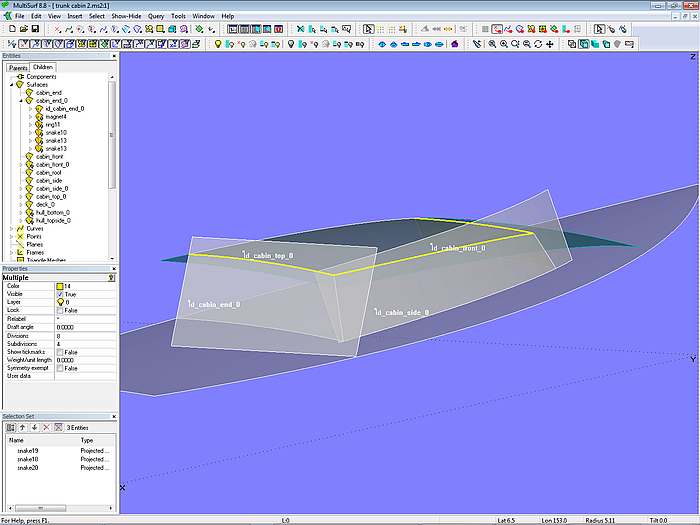
Modell trunk_cabin-2.ms2 – Verwendung von bereits erzeugten SubSnakes für die Trimmed Surface cabin_top
Beim Aufbaudach muß man deren Grundfläche nicht ihrerseits mit den anderen Grundflächen schneiden, sondern man kann die entsprechenden SubSnakes der anderen Flächen auf das Dach projezieren (Projected Snake). Das erspart wiederholte Arbeit.
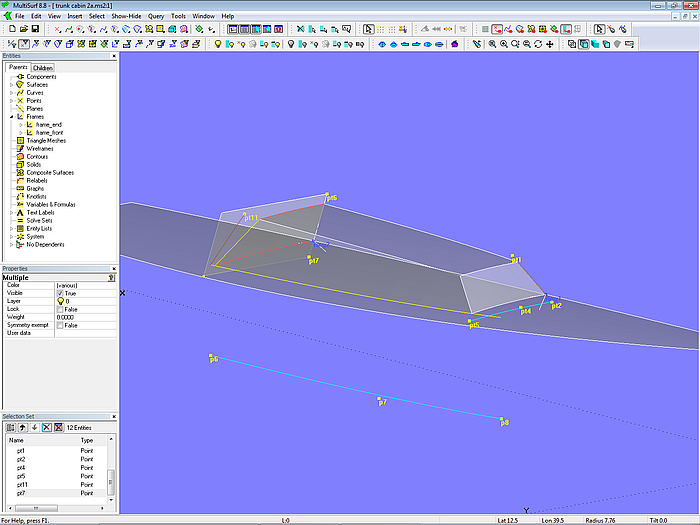
Modell trunk_cabin-2.ms2 – fertige Flächen und ihre definierenden Kurven und Punkte
Es ist zweckmäßig, von den Objekten, die den Aufbau in seiner Form bestimmen, eine Entity List zu machen. Dann kann man rasch all die Punkte und Kurven auf den Bildschirm bringen, die ausschließlich die Form und Lage der einzelnen Flächen kontrollieren. Hilfspunkte wie Ringe zum Trimmen von Intersection Snakes, diese selbst oder SubSnakes brauchen nicht angezeigt werden, das sind nur Sachen im Hintergrund. Von Hauptinteresse ist das fertige Teil und die Kurven und Punkte (Ziehpunkte), die die Form bestimmen.
Die Objekte einer Entity List lassen sich schnell folgendermaßen anzeigen:
- im Entities Manager einen Rechts-Mausklick auf den Namen der Liste, dann im Kontextmenü „Show Parents“ auswählen, oder
- im Entities Manager auf den Namen der Liste klicken, dann in der “Show-Hide”-Toolbar einen Klick auf die Schaltfläche „Show Parents”
Im vorliegenden Modell ist die Unterkante der Aufbauseite eine Projected Snake auf dem Deck. Das hat den Vorteil, daß man unmittelbar erkennt, wo die Seite auf das Deck stößt. Man kann direkt sehen, wie breit das Gangbord ist.
Durch die beiden Ringe wird direkt angegeben, wo Front und Ende des Aufbaus auf MS liegen.
Wird das Deck aber etwas geändert, z. B. die Bucht etwas vergrößert, dann ändert sich die Lage der Snake in der Höhe, und damit wandert die Unterkante Aufbauseite auch etwas nach oben. Zwar bleiben die Ringe auf MS an ihrer Längsposition, aber sie verschieben sich etwas nach oben, ziehen ihre Frames mit, und alles, was davon abhängt.
Im Modell trunk_cabin-3.ms2 sind dagegen alle Basisflächen vom Deck unabhängig. Sie sind im Prinzip in gleicher Weise wie vorangehenden Beispiel definiert, aber die Unterkante Aufbauseite liegt unter der Decksfläche. Auch ist die Lage von Front- und Endfläche nur indirekt durch die Punkte pt2 und pt7 angegeben.
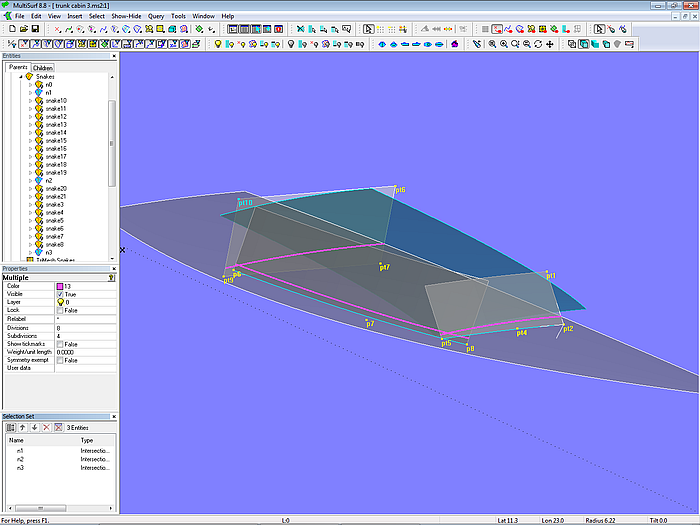
Modell trunk_cabin-3.ms2 – Basisflächen eines Aufbaus, dessen geometrische Form vom Deck unabhängig ist
Wie an den Intersection Snakes erkennbar, werden bei einer Änderung der Decksform die Grundflächen des Aufbaus mehr oder weniger tief in das Deck eintauchen. Aber sonst bleibt die Aufbaugeometrie unverändert. Was sich ändern wird, ist die Gangbordbreite und die Aufbauhöhe über Deck.
3 – Der Freiform-Aufbau
B-spline Lofted Surface mit querlaufenden Mcs
Beim kastenförmigen Aufbau gab es separate Flächen für Front, Seite und Dach. In Modell bubble_cabin_bloft-1.ms2 werden diese 3 Elemente durch eine einzige Fläche vom Typ B-spline Lofted Surface gebildet. Dies ermöglicht runde, weiche Übergange zwischen Aufbaufront, -seite und -dach.
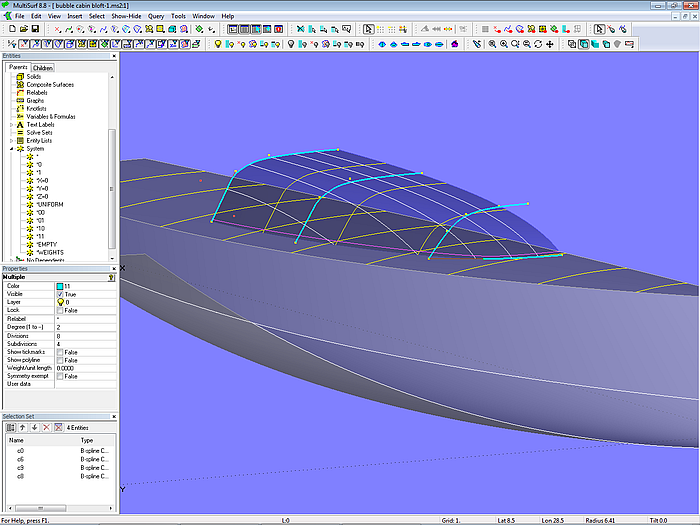
Modell bubble_cabin bloft-1.ms2 – Anordnung der Masterkurven
Die Stützkurven der B-spline Lofted Surface sind hier 4 B-spline Mcs, die in Querrichtung verlaufen. Die Mc-Anordnung ähnelt derjenigen für eine um 90 Grad gedrehte Rumpfhälfte.
B-spline Lofted Surface mit längslaufenden Mcs
In Modell bubble_cabin_bloft-2.ms2 verlaufen die Stützkurven in Längsrichtung. Das ermöglicht, eine Mc als Snake auf das Deck zu legen, so daß man den Aufbau nicht extra am Deck abzuschneiden braucht.
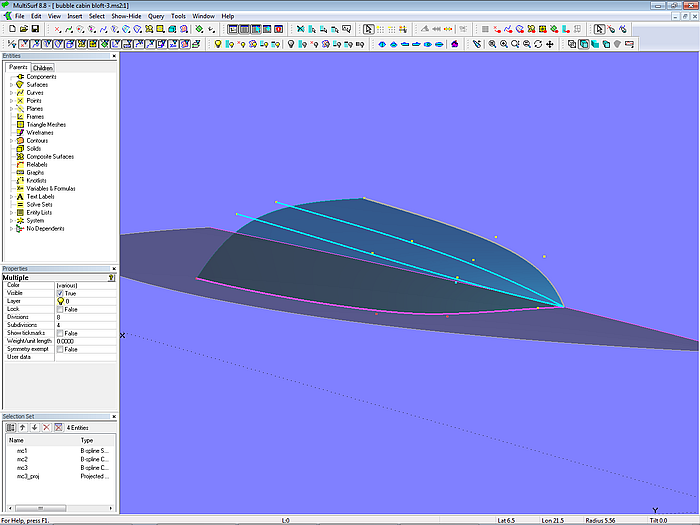
Modell bubble_cabin_bloft-2.ms2 – Anordnung der Masterkurven
Tangent Boundary Surface
Die Konstruktion des ultimativen Bubble-Aufbaus ermöglicht der Flächentyp Tangent Boundary Surface. Zum einen wird die Form durch ihre 4 Randkurven definiert. Zum anderen kann durch innere Kontrollpunkte die Fläche beliebig verformt werden.
Im Modell bubble_cabin_tbs.ms2 wird zuerst die Form der Unterkante des Aufbaus als Kurve c1 erzeugt, diese dann als Projected Snake n0 auf das Deck projeziert. Der Ring r0 teilt die Projected Snake n0 in die beiden SubSnakes n1 und n2. Hinterkante Aufbau bestimmt die B-spline Curve c2, den Verlauf der Kontur auf der Mittschiffsebene die B-spline Curve c3. Damit sind die 4 Randkurven der Tangent Boundary Surface gegeben.
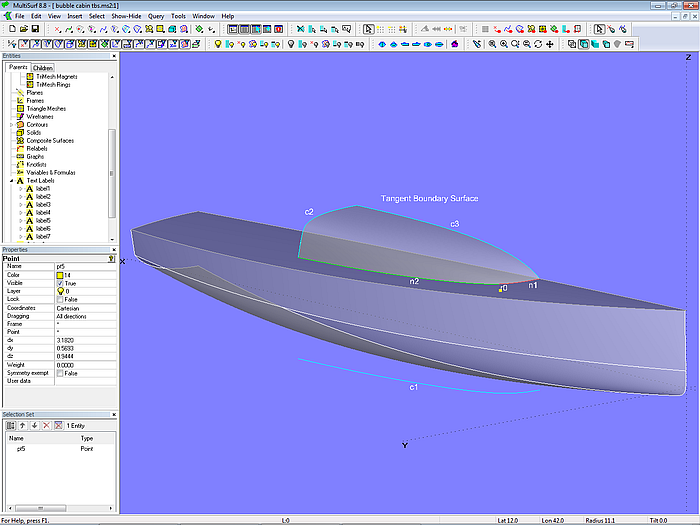
Modell bubble_cabin_tbs.ms2 – Freiform-Aufbau als Tangent Boudary Surface; Anordung der Randkurven
Ist die Form noch nicht wie gewünscht, dann kann über innere Kontrollpunkte (Anzahl in u- und v-Richtung wählbar) die Fläche verändert werden.
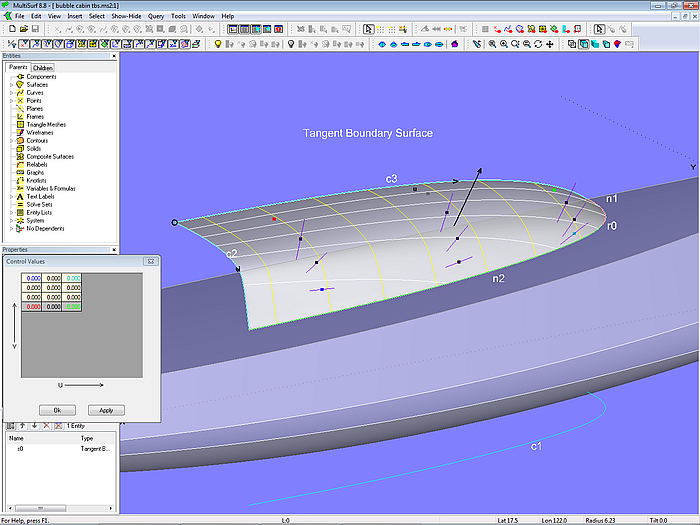
Modell bubble cabin tbs.ms2 – die innere Form einer Tangent Boundary Surface kann durch zusätzliche interne Kontrollpunkte gestaltet werden.
4 - Etwas komplexere Aufbauten
Abgerundete Front
Ein kastenförmiger Aufbau wie in den trunk_cabin-Modellen kann abgerundete Ecken haben. Modell trunk_cabin_cornerpost.ms2 zeigt, wie man so etwas machen kann. Der Grundaufbau ist der gleiche, getrennte Basisflächen für Seite, Front usw. Hinzu kommt die Fläche cabin_front_round vom Typ Rolling Ball Fillet zwischen Frontwand und Seitenwand. Wie der Name andeutet, kann man sich diese Fläche entstanden denken durch eine Kugel, die zwischen beiden Flächen abrollt und dabei eine Abrundung überstreicht, die sich zwischen dem Pfad aller Berührpunkte auf der einen Fläche und dem Pfad aller Berührpunkte auf der anderen Fläche erstreckt.
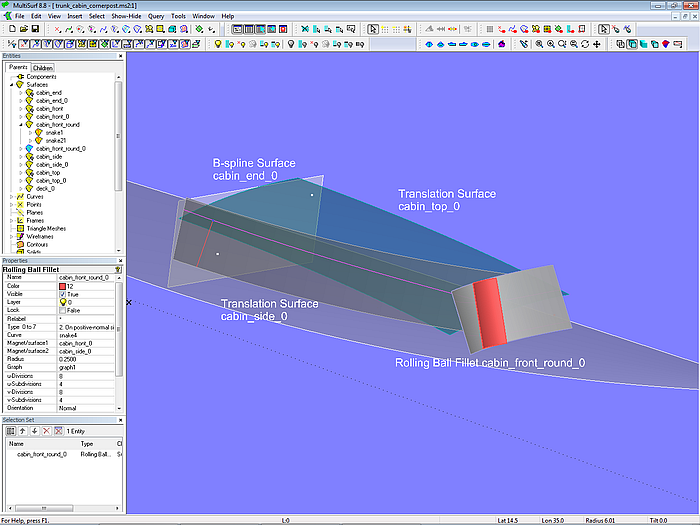
Modell trunk_cabin_cornerpost.ms2 – Basisfläche der Abrundung zwischen Aufbaufront und –seite
Wie bei den anderen Flächen auch wird die Abrundung mit den angrenzenden Flächen zum Schnitt gebracht (Intersection Snakes) und dann der gewünschte Flächenteil als SubSurface oder Trimmed Surface erzeugt.
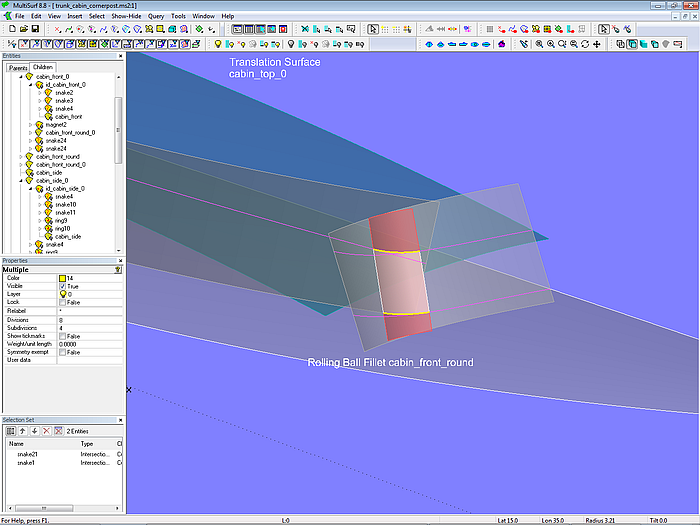
Modell trunk_cabin_cornerpost.ms2 – Abrundung geschnitten an Deck und Aufbaudach (SubSurface)
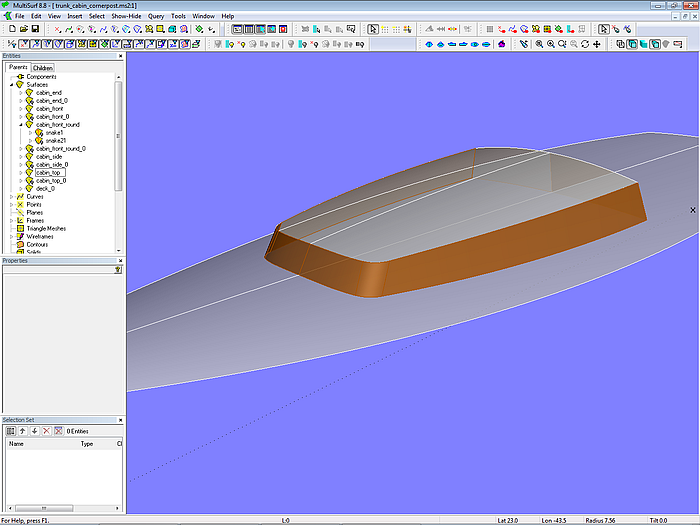
Modell trunk_cabin_cornerpost.ms2 – fertige Aufbauflächen
Abgerundete Aufbaukanten
Mit dem Flächentyp Rolling Ball Fillet lassen sich auch die Kanten entlang des Aufbaudaches abrunden. Modell trunk_cabin_round_edges.ms2 zeigt ein Beispiel.
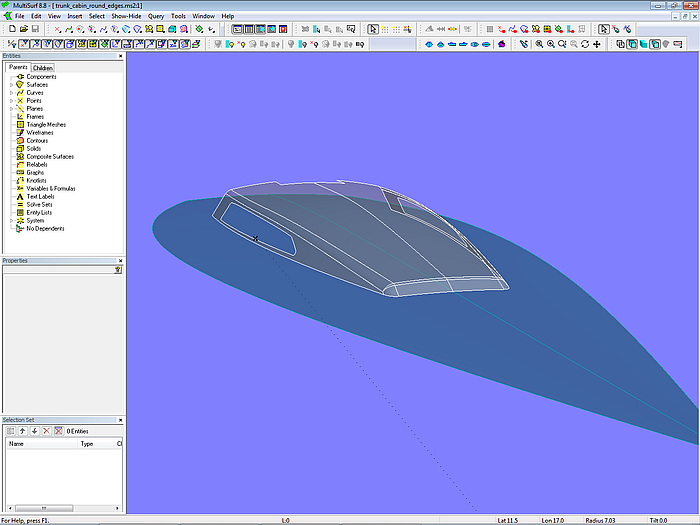
Modell trunk_cabin_round_edges.ms2 – Abrundung der Aufbaukanten mit Rolling Ball Fillets
Zu den Grundflächen des Aufbaus kommen drei Abrundungsflächen hinzu: das Rolling Ball Fillet cab_top_rnd_0 zwischen Aufbaudach cab_top_0 und Aufbaufront cab_front_0, das Rolling Ball Fillet cab_front_rnd_0 zwischen Aufbauseite cab_side_0 und Front sowie das Rolling Ball Fillet cab_side_rnd_0 zwischen Dach und Seite. Alle Fillets haben den gleichen Radius.
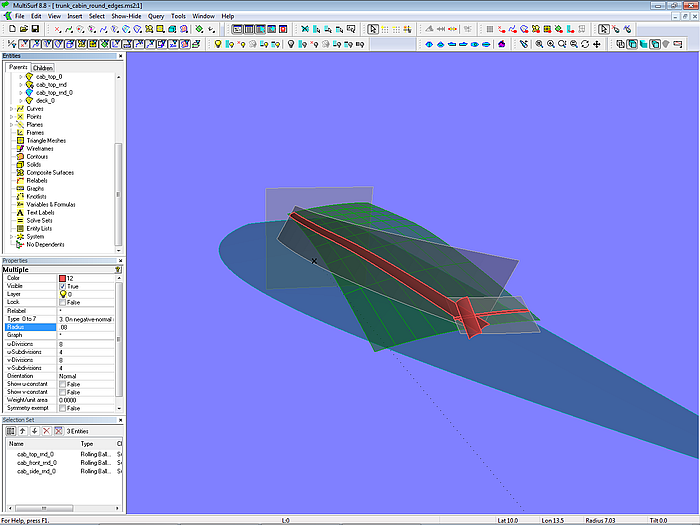
Modell trunk_cabin_round_edges.ms2 – die Abrundungsflächen treffen in der Ecke zwischen Seite, Dach und Front des Aufbaus zusammen.
Die Abrundungen treffen in der Ecke zwischen Dach, Seite und Front aufeinander.
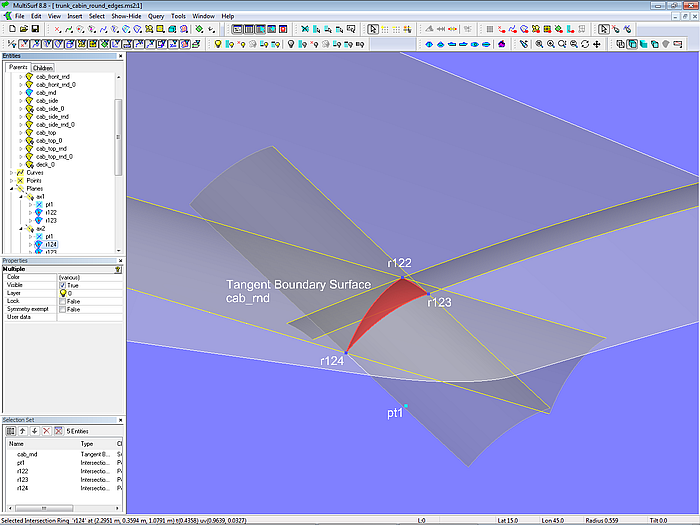
Modell trunk_cabin_round_edges.ms2 – Kugeldreieck zwischen den Abrundungsflächen in der Ecke von Seite, Dach und Front
Die Kugel, die entlang der Durchdringung von Aufbauseite und Aufbaudach rollt, stößt vorne gegen die Frontwand (r123), ihre Abrundungsfläche endet also vor der Front. Läuft die Kugel entlang dem Schnitt von Dach und Front, stößt sie gegen die Seite (r124), ihre Abrundungsfläche endet also vor der Seite. Rollt sie entlang dem Schnitt von Seite und Front, stößt sie gegen das Dach (r122), ihre Abrundungsfläche endet also vor dem Dach. Es entsteht so eine Lücke zwischen den 3 Abrundungsflächen. Geschlossen wird diese Lücke durch einen Teil der Oberfläche der in der Ecke feststehenden Kugel (Mittelpunkt pt1); die Abrundung hier ist ein Kugeldreieck.
Im Modell trunk_cabin_round_edges.ms2 wird dieses Kugeldreieck durch die Tangent Boundary Surface cab_rnd erzeugt.
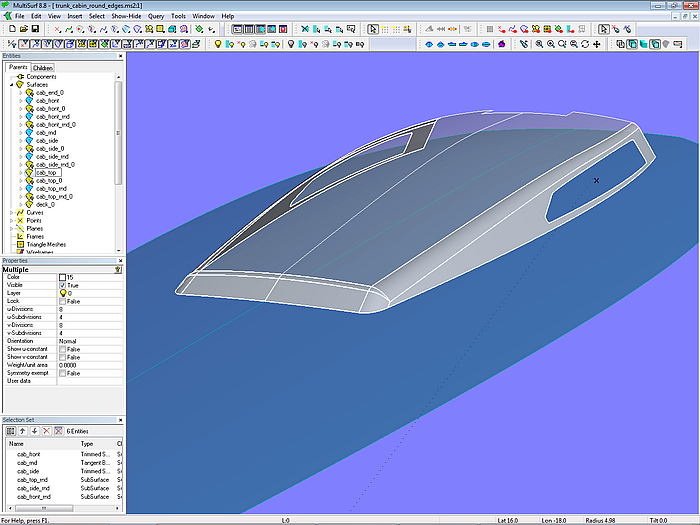
Modell trunk_cabin_round_edges.ms2
Aufbaufront mit ebenen Fenstern
Im Modell front_windows-1.ms2 wird gezeigt, wie sich am einfachsten Flächen für Frontfenster erzeugen lassen. Bedingung ist, daß sie eben und rechtwinklig sein sollen.
Startpunkt ist der XYZRing r0 auf Mitte Deck. Von diesem hängt der Punkt pt2 auf der Mittschiffsebene ab, er kontrolliert die Neigung des inneren Fensters. Zusammen mit dem Punkt pt1 bestimmen sie den 3-point Frame F0, auf den sich dann alle weiteren Punkte beziehen.
Die halbe Breite des Fensters auf MS bestimmt der Punkt pt3. Damit das Fenster rechteckig ist, wird der Copy Point pt4 erzeugt. Mit r0, pt2, pt3 und pt4 ist die B-spline Surface window1_0 bestimmt. (Eine plane rechteckige Fläche läßt sich mit einem Minimum von 4 Punkten und einer B-spline Surface erzeugen, wovon ein Punkt ein Copy Point der anderen 3 Punkte ist.)
Das anschließende Fenster window2_0 ist ebenfalls eine B-spline Surface mit 4 Cps; pt5 ist in Polarkoordinaten definiert, so daß der Radius die Fensterbreite angibt und der Wert Latitude den Winkel zum inneren Fenster.
Das äußere Fenster window3_0 ist in analoger Weise definiert. Soll der Knickwinkel so groß sein wie bei der benachbarten Fläche window2_0, dann muß für den Punkt pt7 der Wert für Latitude das Zweifache des Wertes für pt5 betragen.
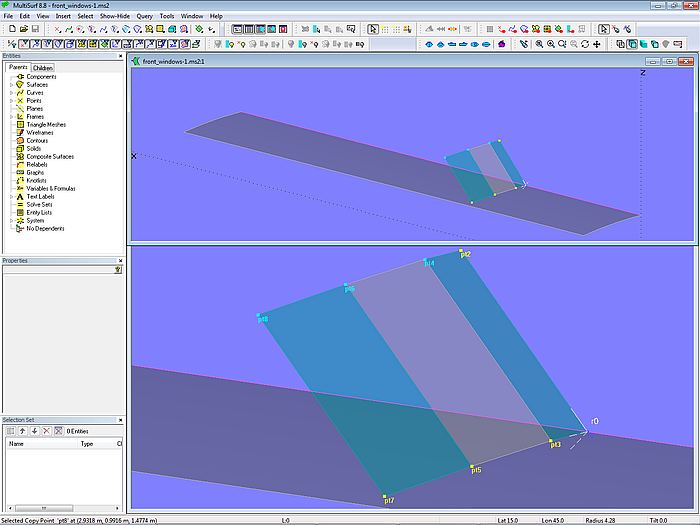
Modell front_windows-1.ms2 – Anordnung der Kontrollpunkte für drei ebene rechtwinklige Fensterflächen
Soll eine der Fensterflächen nicht rechtwinklig sein, sondern am oberen Rand eine andere Breite als am unteren Rand haben, läßt sich das mit der in Modell front_windows-2.ms2 gezeigten Methode einfach bewerkstelligen.
Zwischen den Punkten pt4 und pt6 wird eine Line (line1) aufgespannt, und auf diese der Arc-length Bead e0 gesetzt. Für die B-spline Surface window2_0 ersetzt man dann den Kontrollpunkt pt6 durch e0. Die Fensterfläche ist immer noch plan (sichergestellt durch den Copy Point pt6), aber man kann jetzt die gewünschte obere Breite durch e0 einstellen.
Analog kann man bei der Fensterfläche aussen vorgehen.
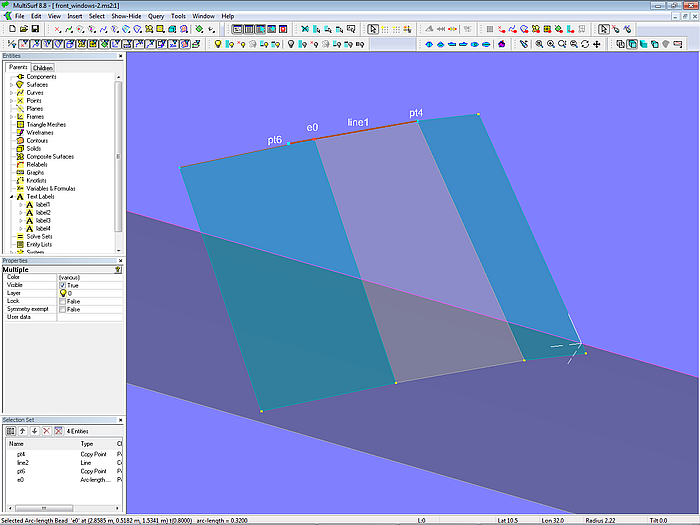
Modell front_windows-2.ms2 – Anordnung der Kontrollpunkte für veränderliche Fensterbreite oben
Modell front_windows-3.ms2 zeigt ein Anwendungsbeispiel.
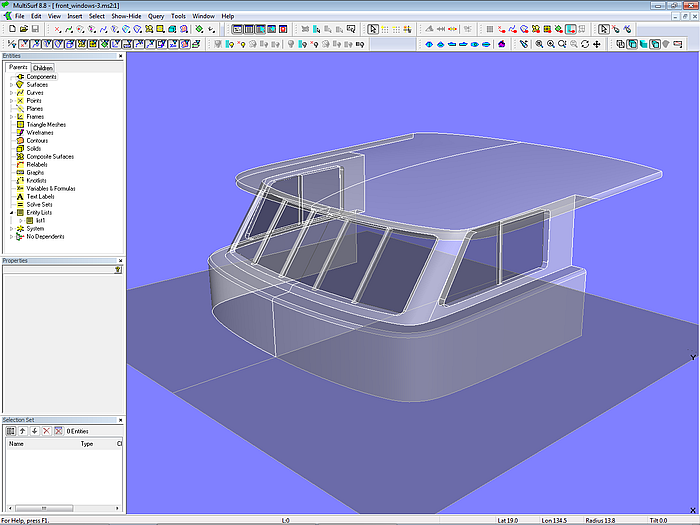
Modell front_windows-3.ms2
5 – Komplexe Aufbauten
Komplexe Aufbauten sind eine Aneinandereihung einfacher Elemente, deren Modellierung in den vorstehenden Abschnitten gezeigt wurden. Hier einige Beispiele.
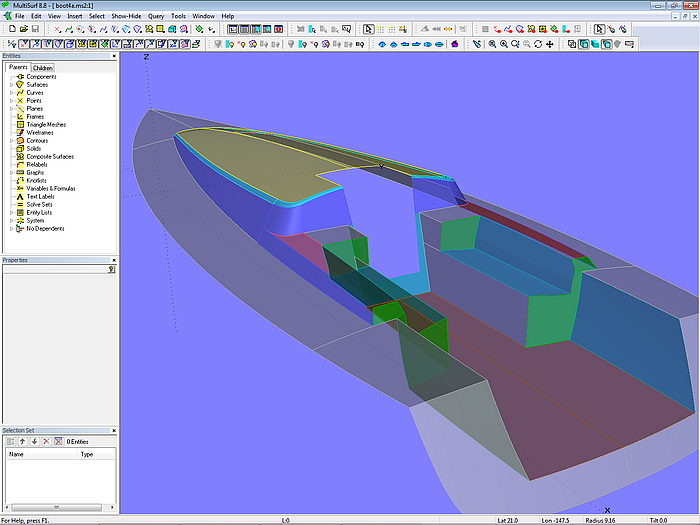
Modell design-4.ms2 - 10 m-Segelboot; Aufbau und Cockpit
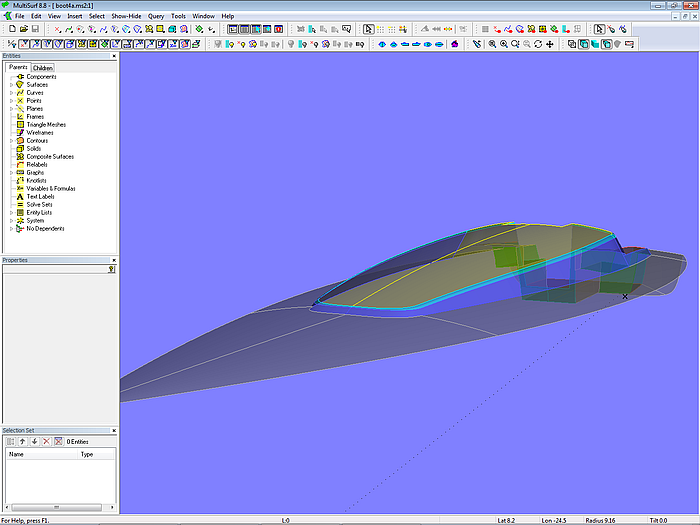
Modell design-4.ms2 - 10 m-Segelboot; Aufbau und Cockpit
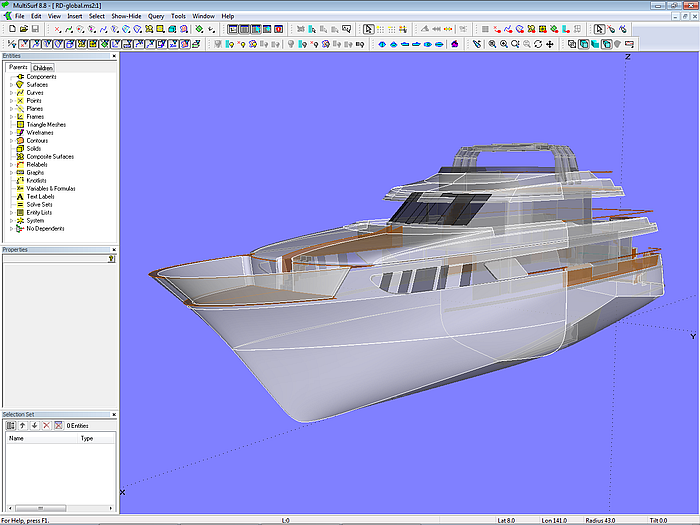
120 ft-Motoryacht (Russel Dowland Design)
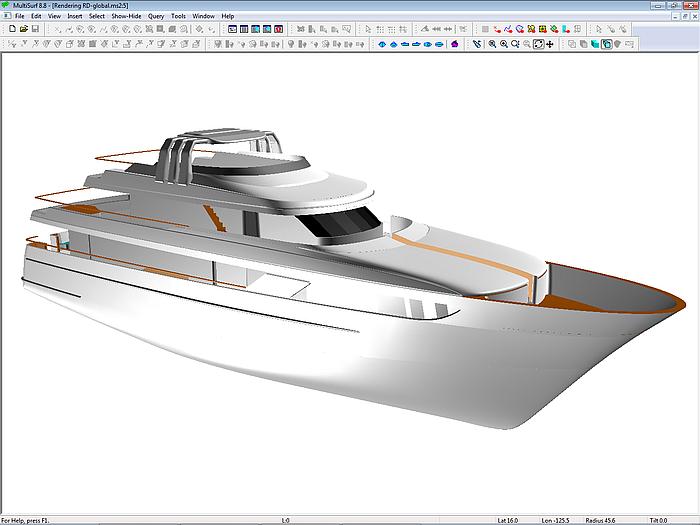
120 ft-Motoryacht (Russel Dowland Design)

10 m-Segelyacht (Juliane Hempel Design)

27 m-Passagierschiff (CL Shipdesign)

11.5 m-Motorboot (CL Shipdesign)