Rechnende Modelle in MultiSurf
Variablen, Formeln und Funktionen
von Reinhard Siegel
Inhalt
Einleitung
Grundkonzept - Variablen, Formeln, Funktionen
- Variablen
- Formeln
- Funktionen
Einfache Anwendungen von Variablen und Formeln
- I-Profil
- Hauptabmessungen
- Segelplan
- Lateralplan
Weiterführende Anwendungen von Variablen und Formeln
- Hydrostatic Reals
- Freie Schwimmlage – ohne Krängung
- Freie Schwimmlage – mit Krängung
- Berechnung des Rumpfwiderstands
- Anordnung der Planken einer klassischen Yacht
- Vermessungsregeln im Modell
Mathematische Funktionen in MultiSurf
Einleitung
Es gibt zwei Möglichkeiten, eine reelle Zahl in der Definition eines Objekts anzugeben: mit einem konstanten Wert oder einer realen Größe. Variablen und Formeln sind Beispiele für reale Größen. Eine Variable trägt einen Wert, der innerhalb eines bestimmten Bereichs liegt. Eine Formel beinhaltet einen Berechnungsausdruck, der aus Variablen, Konstanten, Operatoren und Funktionen besteht. Variablen und Formeln können Eltern aller Objekte sein, die von einem realen Wert abhängig sind.
Welchen Vorteil bieten Variablen und Formeln?
Mit Variablen und Formeln können einfachere, übersichtlichere Modelle erstellt werden. Modelle lassen sich unmittelbar ändern, man muß nicht erst denjenigen Punkt suchen, der eine bestimmte Teilkonstruktion steuert, sondern man kann direkt die Variable auswählen und dann ihren Wert ändern. Beispiel I-Profil: bei gegebener Grundgeometrie bestimmen nur wenige Masse die Form; aber anstatt erforderliche Hilfspunkte einzeln zu konstruieren, können sie durch Rechnung bestimmt werden.
Mit Variablen und Formeln lassen sich Modelle erstellen, die Berechnungen ausführen: Hauptabmessungen, Flächengrößen und Schwerpunkte, Vermessungsmaße, Schwimmlage, hydrostatische Kennwerte, Widerstand und so weiter. Auf diese Weise stellt ein Modell dem Konstrukteur erheblich mehr zusätzliche Informationen bereit, die bei Änderung unmittelbar aktualisiert werden.
Variablen und Formeln erweitern die Funktionalität von MultiSurf enorm - sie machen MultiSurf grenzenlos.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point)
Mc: Masterkurve, Stützkurve (master curve, support curve)
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
Grundkonzept – Variablen, Formeln, Funktionen
Variablen
Wenn ein normaler 3D-Punkt in MultiSurf erstellt wird, müssen seine Koordinaten dx, dy und dz eingegeben werden. In der Regel wird eine konkrete Zahl, z. B. 1.2345, verwendet, um den Wert einer Koordinate anzugeben. Andererseits kann man statt einer Zahl auch eine Variable verwenden, ein Symbol für jedes Element einer bestimmten Menge.
Betrachten wir das Modell box-1.ms2, einen kastenförmigen Körper.
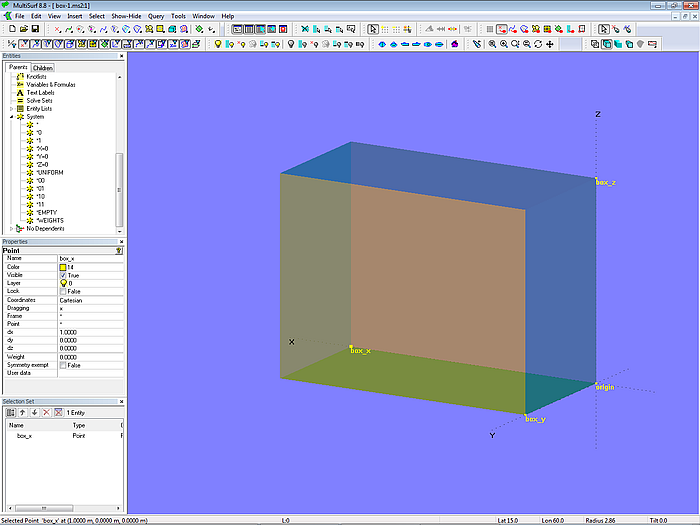
Modell box-1.ms2 – quaderförmiger Kasten
Seine Länge wird durch Point box_x, die Breite durch Point box_y und die Höhe durch Point box_z bestimmt. Die dx-, dy-, dz-Koordinatenwerte sind (1; 0; 0), (0; 0; 0,5) und (0; 0; 0,75). Wenn man einen dieser Punkte verschiebt, werden die entsprechenden Abmessungen des Quaders geändert.
Das Modell box-2.ms2 sieht identisch aus. Allerdings sind nun die Abmessungen mit den 3 Variablen length, breadth und height bestimmt. Zum Beispiel ist für die dx-Koordinate des Punktes box_x nicht der Zahlenwert 1 eingetragen, sondern die Variable length.
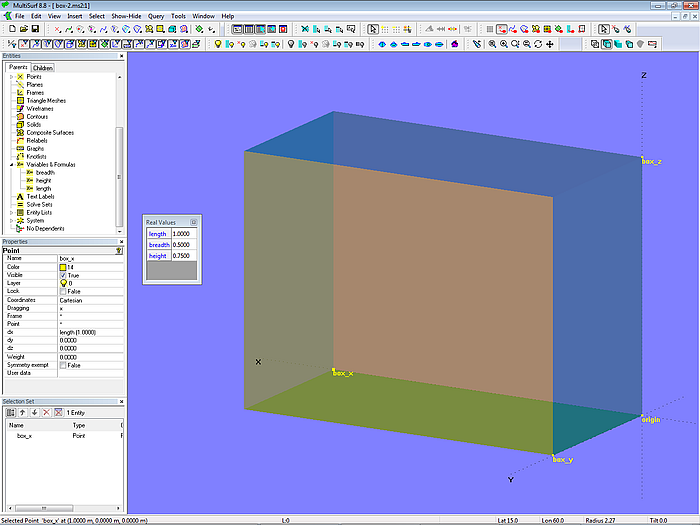
Modell box-2.ms2 – 3 Variablen legen die Abmessungen des Quaders fest.
Um alle Variablen in einem Modell anzuzeigen, kann man „Tools/ Real Values“ im Hauptmenü auswählen, oder als Abkürzung einfach die Taste „V“ drücken. Im dann angezeigten „Real Values“-Dialogfenster kann der momentane Wert einer Variablen direkt geändert werden. Oder man wählt die Variable im Enities Manager aus und editiert sie dann im Properties Manager.
Im Gegensatz zu Punkten, die man manuell am Bildschirm nur verschieben kann, wenn sie sichtbar sind, können mit Variablen definierte Objekte ausgeblendet sein. Beispielsweise einfach ihren Wert im „Real Values“- Fenster ändern und schon paßt sich das Modell an.
Variablen können Eltern sein von allen Objekten, die von einem realen Wert abhängen. Darum können sie Eltern sein von Punkten (als Koordinaten, Offsets, Winkel, t-, u- und v-Parameterwerten), sowie von Kurven und Flächen (via Knotlists und Weights).
Bei allen Geometrien, deren generelle Form feststeht, aber konkrete Abmessungen noch offen sind, lassen sich Variablen vorteilhaft verwenden. So zum Beispiel für Querschnittmaße von Längspanten, Höhe und Breite einer Fußreling, dem Radius der Abrundung zwischen Flächen im Cockpit, usw.
Formeln
Einer Variablen ist stets ein bestimmter Wert zugewiesen (box-2.ms2). Soll beispielsweise die Länge des Quaders immer das Zweifache seiner Höhe betragen, kann diese Bedingung aber nicht mit einer Variablen in das Modell eingebaut werden. Stattdessen muß das Objekt Formula (Formel) verwendet wer-den. Formeln liefern das Ergebnis einer Berechnung mit Konstanten, Variablen und Funktionen.
Im Modell box-3.ms2 ist die veranschaulicht.
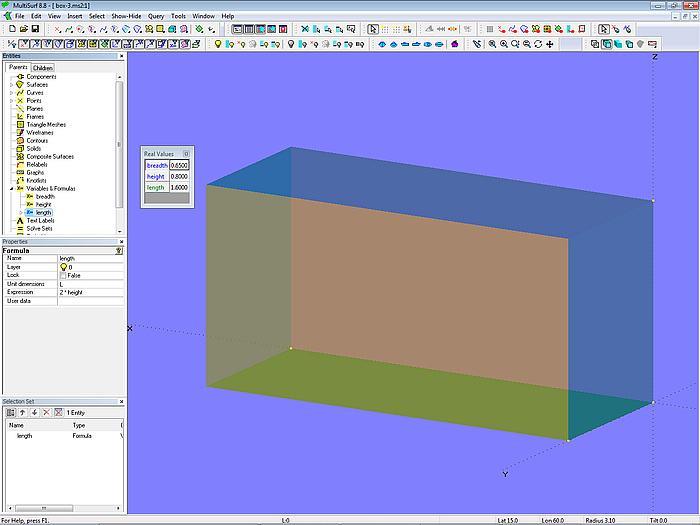
Modell box-3.ms2 – mit Hilfe der Formel length wird festgelegt, dass die Abmessung des Quaders in X-Richtung immer das Zweifache seiner Höhe ist.
Im „Real Values“–Dialogfenster werden die Namen von Variablen und Formeln in unterschiedlicher Farbe angezeigt. Nur die Werte der Variablen können hier geändert werden, für Formeln wird das Ergebnis der Rechenanweisung angezeigt.
Modell box-3.ms2 ist nur ein einfaches rechnendes Modell. Mit Variablen und Formeln lassen sich komplexe Modelle erzeugen, die zum Beispiel Vermessungsmaße, Druckpunktlage, Schwimmlage usw. ermitteln.
Funktionen
Wesentlicher Bestandteil von Formeln sind Funktionen (Functions), die im Rechenausdruck verwendet werden können. Mit Funktionen lassen sich die dx, dy, dz-Koordinaten eines Punktes bestimmen, der Abstand zwischen 2 Punkten ermitteln, man kann quadrieren, Wurzelziehen usw. Oder beispielsweise die Größe einer Fläche berechnen, wie im Modell area-1.ms2 demonstriert wird.
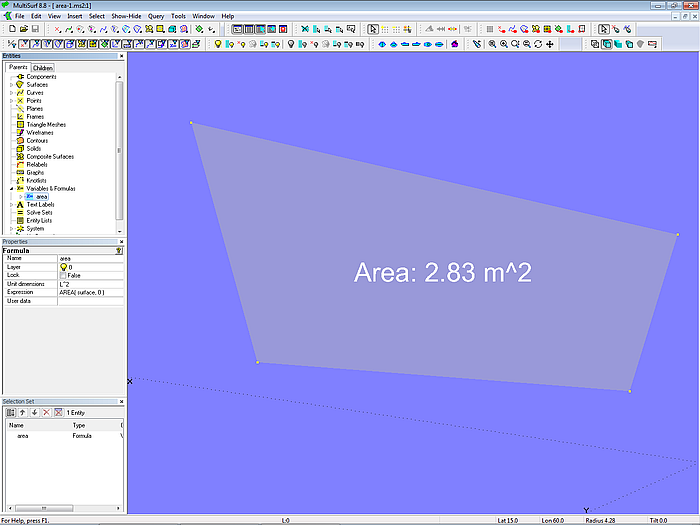
Modell area-1.ms2 – Anwendung der Funktion AREA
Wird die Form der Fläche durch Verschieben der Kontrollpunkte geändert, wird die Flächengröße neu berechnet und mit einen Text Label angezeigt.
Häufig verwendete Funktionen
In Formeln werden häufig folgende Funktionen verwendet:
- XPOS, YPOS, ZPOS: gibt die XYZ-Position eines Punktes an
- TPOS gibt die t-Position eines Punktes an
- ARCLEN: bestimmt die Bogenlänge zwischen zwei Kurvenpunkten
- DIST: bestimmt den Abstand zwischen zwei Punkten
- AREA: berechnet die Größe einer Fläche
- CENTROID: ermittelt die XYZ-Koordinaten des Schwerpunkts einer Fläche
- HYDRO: liefert hydrostatische Werte (für feste Schwimmlage; in Kombination mit dem Objekt Solve Set auch für Schwimmlagen mit freier Tauchung und freiem Trimm)
Die Liste aller in MultiSurf zur Verfügung stehenden Funktionen befindet sich am Ende dieses Tutorials.
Funktion DIST
Betrachten wir hierzu ein einfaches Beispiel: das Modell wl_length.ms2.
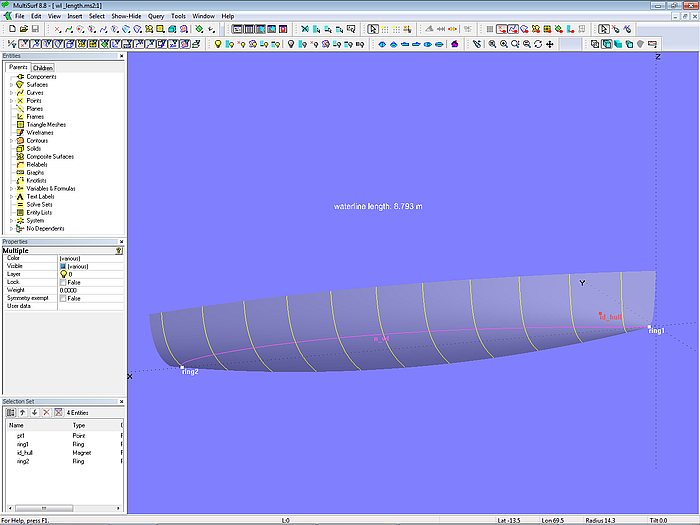
Modell wl_length.ms2 - Berechnung der Wasserlinienlänge
Das Modell enthält die Fläche hull eines Bootsrumpfs. Dessen Wasserlinienlänge soll ermittelt werden.
- Erzeuge Magnet id_hull im Bugbereich
- Schneide den Rumpf mit der *Z = 0 – Ebene. Dies ist die Intersection Snake n_wl.
- Setze ring1 an den Anfang der Snake.
- Setze ring2 an das Ende der Snake.
- Erzeuge die Formel wl_length mit diesem Rechenausdruck:
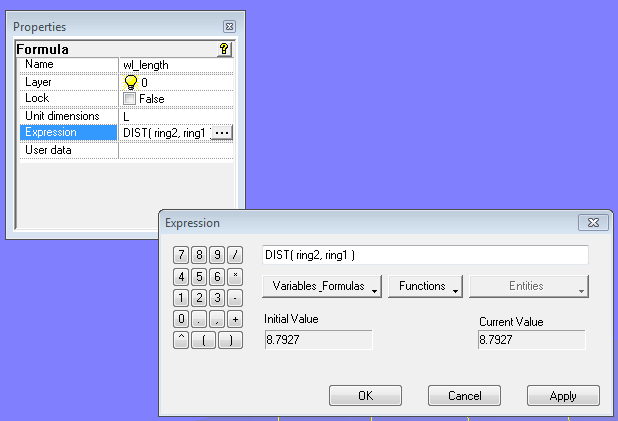
Der in der Formel wl_length verwendete Rechenausdruck, um den Abstand zwischen den Wasserlinienenden zu berechnen
Mit der Funktion DIST wird der Abstand zwischen den beiden Ringen berechnet. (Man beachte, dass hier bei der Verwendung der DIST-Funktion angenomen wird, dass beide Ringe die Koordinaten Y = 0 und Z = 0 haben.)
Um das Ergebnis unserer Berechnung anzuzeigen (d. h. den Wert von Variablen und Formeln), gibt es Möglichkeiten:
- Real Values
- Text Label
Zur Anzeige von Real Values kann man „Tools/ Real Values“ im Hauptmenü auswählen, oder als Abkürzung einfach die Taste „V“ drücken.
Um mit einem Text Label den Wert einer Variablen oder einer Formel darzustellen, sind diese Schritte nötig:
- Erzeugen eines Punktes, der als Bezugspunkt des Text Labels dient (im Modell wl_length.ms2 ist dies Point pt1)
- Einfügen eines Text Label-Objekts. Über die Eigenschaft "Legend" wird die Beschreibung sowie die Formatierung des angezeigten Wertes festgelegt.
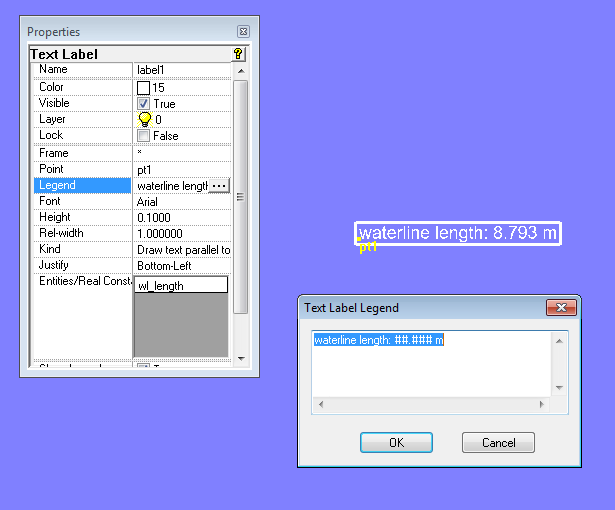
Anzeige des Wertes von Variablen und Formeln mit Hilfe eines Text Labels
Funktion TPOS, XPOS, YPOS, ZPOS
Modell positions.ms2 zeigt, wie die XYZ-Koordinaten eines Punkts und der t-Parameter-Wert eines Beads oder eines Rings ermittelt werden. Die Formel t_e1 liefert den t-Parameter von Bead e1; die Rechenanweisung lautet einfach: TPOS (e1). Die Formel x_e1 gibt die X-Koordinate von Bead e1 zurück; der Rechenausdruck ist: XPOS (e1). Entsprechend lauten die Funktionen für die Y- und Z-Koordinaten YPOS und ZPOS.
Funktion AREA, CENTROID
Ähnlich wie im bereits gezeigten Beispiel wird im Modell area-2.ms2 die Größe einer Fläche mittels der Funktion AREA berechnet. Zusätzlich werden mit der Funktion CENTROID die Koordinaten des Flächenschwerpunkts ermittelt. Mit diesen Ergebnissen ist der Punkt CE definiert.
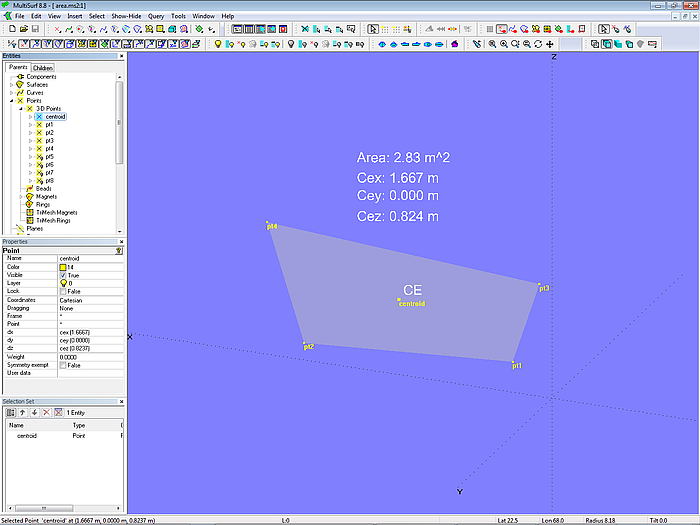
Modell area-2.ms2 – Anwendung der Funktionen AREA und CENTROID
Die Formel area verwendet in ihrer Rechenanweisung die Funktion AREA (surface, use_sym). Sie benötigt zwei Argumente: den Namen der Fläche sowie die Zahl 0 oder 1, abhängig von der Verwendung der Modellsymmetrie (0 = keine Symmetrie; 1 = Symmetrie verwenden). Im Beispiel hier lautet für die Formel area der Rechenausdruck: AREA (s0, 0).
Die Funktion für den Flächenschwerpunkt ist: CENTROID (entity, use_sym (0 oder 1), index (1-3, für X, Y, Z-Koordinate). Sie benötigt also drei Argumente. Mithin lauten die Ausdrücke für die den Punkt ce definierenden Formeln: cex: CENTROID (s0, 0, 1), cey: CENTROID (s0, 0, 2), cez: CENTROID (s0, 0, 3).
Funktion ARCLEN
Modell arc_length.ms2 gibt ein Beispiel für die Funktion ARCLEN an. Diese ermittelt die Bogenlänge zwischen zwei t-Positionen auf einer Kurve. Sie benötigt 3 Argumente: den Namen der Kurve und die beiden t-Positionen. Die Formel length_01_05 berechnet beispielsweise die Bogenlänge der Kurve c0 zwischen t = 0.1 und t = 0.5. Somit lautet der Rechenausdruck für die Formel length_01_05: ARCLEN (c0, 0.1, 0.5).
Wenn die Bogenlänge zwischen zwei Beads oder Rings auf einer Kurve oder Snake ermittelt werden soll, kann die Funktion TPOS verwendet werden. TPOS gibt den t-Parameter-Wert eines Beads oder Rings zurück.
Im Modell arc_length.ms2 liegen auf der Kurve c0 die Beads e1 und e2. Die Formel length_e1_e2 berechnet die Bogenlänge zwischen diesen beiden Beads. Der Berechungsausdruck von length_e1_e2 lautet damit: ARCLEN (c0, TPOS (e1), TPOS (e2)).
Einfache Anwendungen von Variablen und Formeln
I-Profil
Das Modell I-beam.ms2 ist im „Examples“-Ordner von MultiSurf enthalten. Es zeigt, wie sich ausgehend von 4 Variablen für Höhe, Breite sowie Dicken eines I-Profils (Doppel-T-Profil) die Eckpunkt-Koordinaten des Stegs und der beiden Gurte ermitteln lassen. Die dafür benutzten Formeln d1, d2 und d3 verwenden nur einfache Arithmetik im jeweiligen Rechenausdruck.
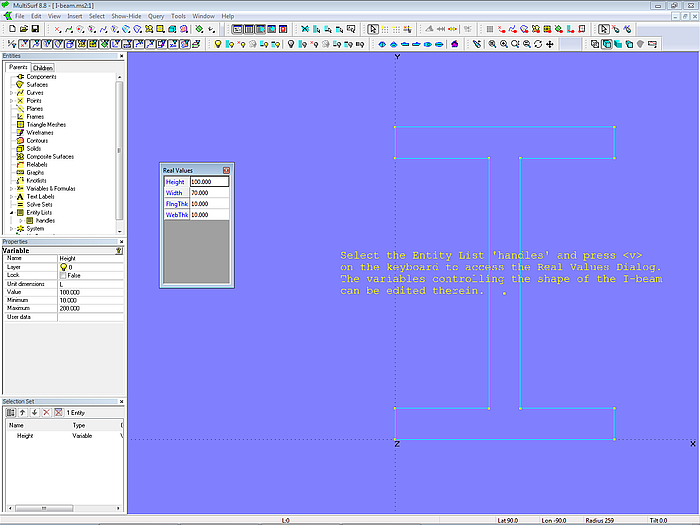
Modell I-beam.ms2 (aus dem MultiSurf “Examples-Ordner") – 4 Variablen definieren die Abmesungen des Profils, drei Formeln ermitteln die Koordinaten der Eckpunkte.
Hauptabmessungen
Das Modell main_dimensions.ms2 berechnet die Hauptabmessungen eines Rumpfes. Im Wesentlichen werden in den Formeln die Funktionen XPOS, YPOS und ZPOS verwendet, um die XYZ-Koordinaten von Punkten zu bestimmen. Mit diesen werden dann zum Beispiel die Länge über alles, die Länge in der Wasserlinie, vorderer und hinterer Überhang etc. ermittelt.
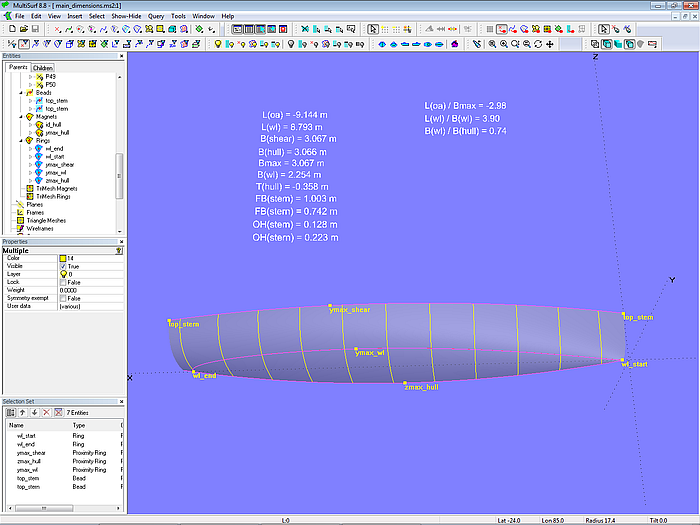
Modell main_dimensions.ms2
Die maximale Decksbreite und die größte Breite in der Wasserlinie wird jeweils mit Hilfe eines Proximity Rings ermittelt. Hierbei wird automatisch derjenige Kurvenpunkt mit dem größten Abstand von der Mitt-schiffsebene gesucht.
Eine Reihe von Text Labels zeigt die Ergebnisse an.
Segelplan
Das Modell sailplan.ms2 zeigt einen Segelplan, dessen Geometrie durch Eingabe der Abmessungen von Rigg und Segel bestimmt wird. Mit Hilfe von Formeln werden für Groß- und Vorsegel sowie für beide zusammen Fläche und Schwerpunkt berechnet.
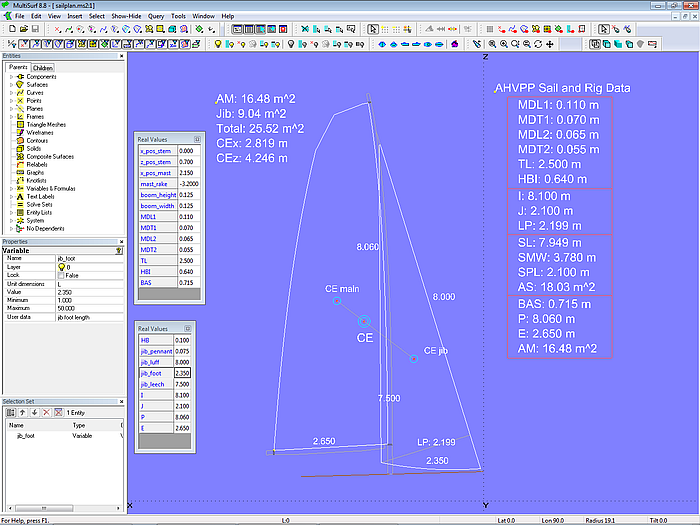
Modell sailplan.ms2 - im Real Values-Fenster können Rigg- und Segelmasse editiert werden.
Die Entity Lists edit_rig_dimensions und edit_sail_dimensions enthalten Variablen für Rigg und Segel. Im Entities Manager eine der Listen auswählen, dann das Real Values-Anzeigefenster öffnen mit Taste "V" oder Hauptmenü/ Extras/ Real Values. Hier können neue Werte eingegeben werden. Ändert man bei-spielsweise die Länge des Unterlieks des Vorsegels, wird der Segelplan entsprechend angepaßt. Segel-flächen, Gesamtfläche, Schwerpunkt usw. werden aktualisiert. Direkt stehen so dem Konstrukteur wert-volle Informationen zur Verfügung.
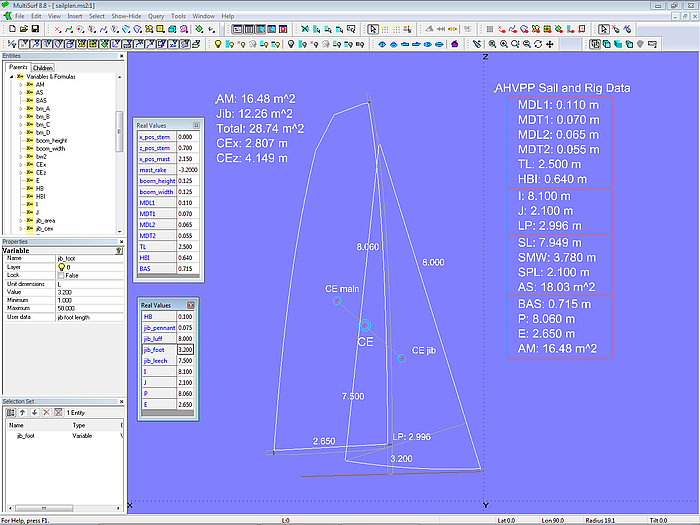
Modell sailplan.ms2 – Vorsegel mit längerem Unterliek; automatisch werden alle davon betroffenen Daten neu berechnet.
Lateralplan
Das Modell lateralplan.ms2 zeigt, wie sich Entwurfsdaten für den Lateralplan des Unterwasserschiffs eines Segelboots mit Hilfe von Variablen und Formeln berechnen lassen. Die unter der Wasserlinie lie-genden Flächenteile von Rumpf und Ruder werden zunächst mit SubSurfaces definiert, anschließend diese dann auf die Mittschiffsebene projeziert als Projected Surfaces. Die Kielfläche kann direkt projeziert werden.
Dann werden analog zum Segelplan die Einzelflächen und -schwerpunkte sowie die Gesamtgröße und Schwerpunktlage des Lateralplans bestimmt. Durch Kreise um Punkte mit Koordinaten entsprechend der Formel-Werte werden die Schwerpunktlagen veranschaulicht.
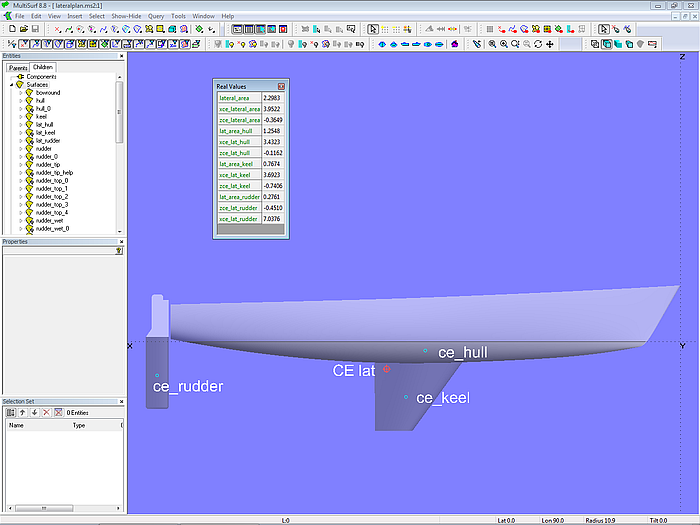
Modell lateralplan.ms2 – Berechnung von Größe und Schwerpunkt der Lateralfläche von Rumpf, Kiel und Ruder
Weiterführende Anwendungen von Variablen und Formeln
Hydrostatic Reals
Unter den Variablen und Formeln, die MultiSurf zur Verfügung stellt, gibt es einen speziellen Typ – Hydrostatic Reals. Mit Hydrostatic Reals ist es möglich, hydrostatische Formwerte für eine mit Tauchung, Trimm und Krängung vorgegebene Schwimmlage während der Arbeit an der Rumpfform anzuzeigen. Hydrostatic Reals ermöglichen es auch, für vorgegebenes Gewicht und Schwerpunktlage die Schwimmwasserlinie zu bestimmen. Dies ist zum Beispiel von Vorteil für die Beurteilung der Wasserlinienform bei verschiedenen Beladungszuständen. Ebenso kann die tatsächliche Wasserlinie bei Krängung angezeigt werden, was sehr praktisch ist, um zu prüfen, ob der Spiegel eintaucht.
Die Eltern für Hydrostatic Reals sind:
- Sp. Gravity
- Zcg
- Sink
- Trim
- Heel
- Type
- Contour List
Die ersten 5 Eltern sind die gleichen, die bei der Berechnung der Hydrostatik via Hauptmenü/ Tools/ Hydrostatics eingegeben werden.
Type gibt an, welcher Hydrostatikwert berechnet wird. Es gibt insgesamt 29 Typen, identisch mit den unter Tools/ Hydrostatics angegebenen Werten.
Contour List gibt den Namen einer Entity List an, die die Namen der Spantkonturen enthält, die zur Berechnung der Hydrostatic Reals verwendet werden. Diese Konturen können ausgeblendet sein, was sehr praktisch ist, damit die Bildschirmanzeige übersichtlich bleibt.
Im Modell Hydro_reals_example-1.ms2 gibt es die C-spline Lofted Surface hull_0. Damit die Spanten geschlossen sind, außerdem die Ruled Surface deck_0. In Contour List ist die Entity List Hydro_contours angegeben. Sie enthält die 3 Spantkonturen hydro_stations1, hydro_stations2 und hydro_stations3, die jeweils hull_0 und deck_0 schneiden.
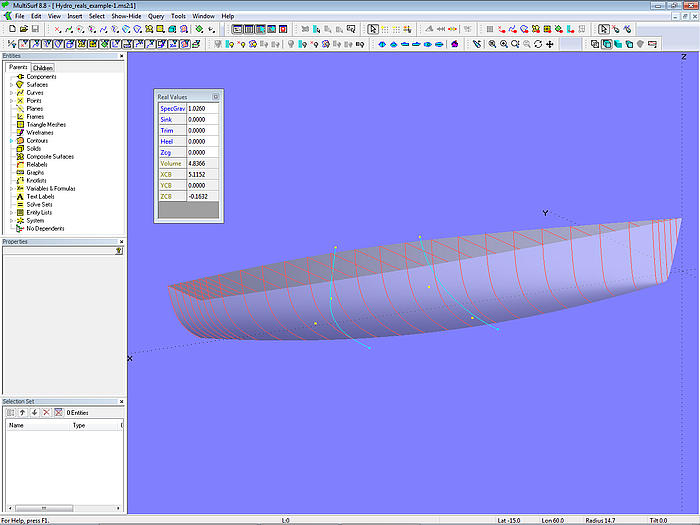
Modell Hydro_reals_example-1.ms2 – Berechnung der Hydrostatikwerte mit Hilfe des speziellen Formeltyps Hydrostatic Reals
Der Grund für die Verwendung einer Gruppe von 3 Spantkonturen mit unterschiedlichen Spantabständen besteht darin, damit die Genauigkeit der Ergebnisse zu verbessern, wenn sich die Rumpfform schnell ändert. Ein sehr enger Spantabstand verzögert die Programmantwort.
Das Modell Hydro_reals_example-1.ms2 berechnet die Hydrostatikwerte von Volumen, XCB, YCB und ZCB. Wenn das Modell geöffnet ist, die Taste "V" drücken oder über Hauptmenü/ Tools/ Real Values auswählen, um das Real Values-Fenster anzuzeigen. Sowie eine Mastercurve und damit die Rumpfform geändert wird, werden hier die neuen Werte angezeigt. Über das Real Values-Fenster läßt sich auch die Schwimmlage ändern, beispielsweise in dem man einen anderen Wert für Sink eingibt – umgehend werden die neuen Formwerte angezeigt.
Alle verfügbaren Formwerte mit Hilfe der Hydrostatic Reals werden im Modell Hydro_real_example-3.ms2 ermittelt.
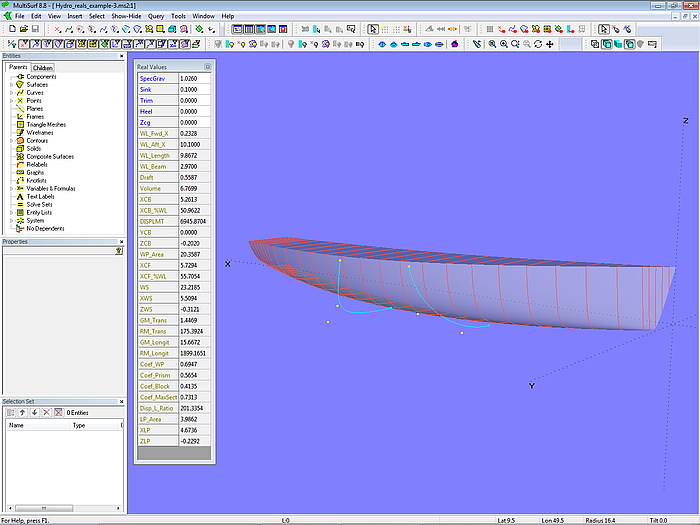
Modell Hydro_reals_example-3.ms2
Soweit die Einführung, wie sich mit Hydrostatic Reals die hydrostatischen Eigenschaften eines Rumpfes berechnen lassen.
Freie Schwimmlage – ohne Krängung
Im vorherigen Modell wurden die Hydrostatikwerte für eine vorgegebene Position des Bootes im Wasser berechnet. Darüber hinaus kann mit Hydrostatic Reals in Kombination mit dem Objekt Solve Set die Frage beantwortet werden, welche Schwimmlage das Boot bei gegebenem Gewicht und Schwerpunkt ein-nehmen wird. Dabei ändert das Solve Set-Objekt systematisch Tauchung (Sink) und Trimm (Trim), bis ein Gleichgewicht zwischen den Kräften und Momenten von Gewicht und Auftrieb besteht.
Das Modell Hydro_free_floating.ms2 ähnelt im Wesentlichen dem vorherigen Beispiel. Wiederum gibt es die C-spline Lofted Surface hull_0 und die Ruled Surface deck_0, die von den Spantkonturen hydro_stations1, hydro_stations2 und hydro_stations3 geschnitten werden. Diese sind in der Entity List Hydro_contours enthalten, die ihrerseits für Contour List eingetragen ist.
Der Point mass_boat repräsentiert das Gewicht des Bootes und dessen Schwerpunkt. Nehmen wir an, dass das fertige Boot geschätzt 5200 kg wiegt und der Gewichtsschwerpunkt in Längsrichtung bei 5,25 m liegt. Die Eigenschaft Weight des Punktes mass_boat erhält also den Wert 5200 (kg). Für die Längenposition (Koordinate dx von mass_boat) gibt die Variable Xcg, deren Wert zunächst mit 5,25 (m) eingetragen ist.
Um das Boot frei schwimmend darzustellen, gibt es den Roll-Pitch-Yaw-Frame F_float. In dieses schiffsfeste Koordinatensystem ist die Rumpffläche hull_0 kopiert, einmal als Copy Surface hull_float_stb und einmal als Copy Surface hull_float_ps.
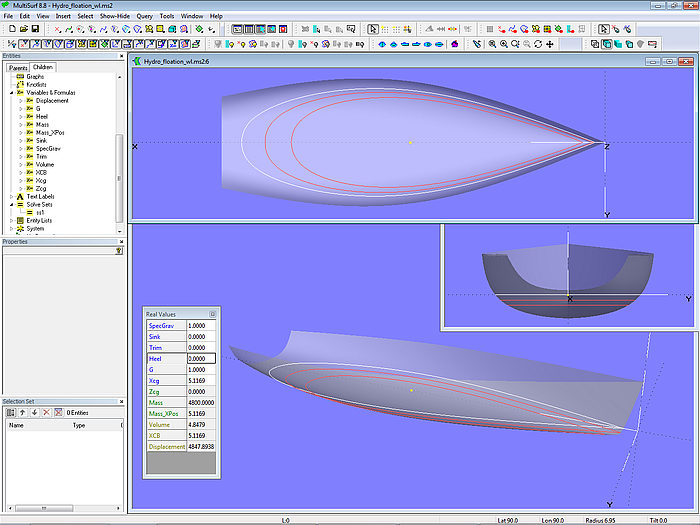
Modell Hydro_free_floating.ms2 – freie Schwimmlage bei Gleichgewicht von Gewicht und Auftrieb
Wenn das Modell geöffnet ist, kann das Fenster für "Real Values" angezeigt werden (Taste "V" oder Hauptmenü/ Tools/ Real Values). Wenn man dann im Entity-Manager die Kategorie Solve Sets öffnet und hier den Solve Set ss1 auswählt, zeigt ein Blick auf den Properties Manager, dass Type momentan auf "Dormant" eingestellt ist. Dies bedeutet, dass Solve Set ss1 ist nicht aktiv, es führt kein Gleichgewicht von Gewicht und Auftrieb durch Variation von Tauchung und Trimm herbei.
In der aufrechten Schwimmlage (Heel = 0) mit Sink = 0 und Trim = 0 ist das Volumen 4,84 m ^ 3, das Deplacement beträgt 4961 kg und XCB liegt bei 5,12 m.
Das geschätzte Bootsgewicht beträgt jedoch 5200 kg und Xcg liegt bei 5,25 m. Welche Schwimmlage tritt nun in dieser Situation ein?
Für die Antwort muß der Solve Set ss1 auf "Active" eingestellt werden. Tauchung und Trimm werden nun so geändert, bis das Deplacement dem Gewicht des Bootes entspricht und XCB und Xcg bezogen auf die Wasseroberfläche senkrecht übereinander liegen. Dies ist hier der Fall bei einer Tauchung (Sink) von -0,024 m und einer Vertrimmung (Trim) von 0,37 Grad. Jetzt weiß man, wie groß die Unterschiede bei Sink und Trim zwischen vorhandenem und geplantem Deplacement sind. Nun ist die Frage zu beantworten: den Rumpf so lassen oder ändern.
Freie Schwimmlage – mit Krängung
Ein verwandtes Problem besteht darin, die Schwimmlage bei Krängung zu kennen. Dahin gestellt sei, ob dafür das Motiv die Beurteilung der asymmetrischen Form der Wasserlinien ist, oder die Frage, wie weit der Spiegel frei von der Wasseroberfläche bleibt oder bereits eintaucht. Krängung bei festgehaltener Tauchung und Vertrimmung führt zu falschen Ergebnissen, da das verdrängte Volumen zunimmt. Um realistische Antworten zu erhalten, muß das Boot bei Krängung frei schwimmen.
Das Modell Hydro_free_floating.ms2 ist bereits für die Antwort eingerichtet. Man muß nur noch den Krängungswinkel eingeben, beispielsweise 15 Grad. Dazu kann man entweder im Entities-Manager die Kategorie Variables and Formulas öffnen, hier die Variable Heel auswählen und im Properties Manager den gewünschten Wert eingeben. Oder man gibt die Krängung direkt über das Fenster "Real Values" ein. Der aktive Solve Set ss1 sorgt dafür, das Sink und Trim entsprechend den Gewichtsverhältnissen angepaßt wird, die durch den Punkt mass_boat definiert sind.
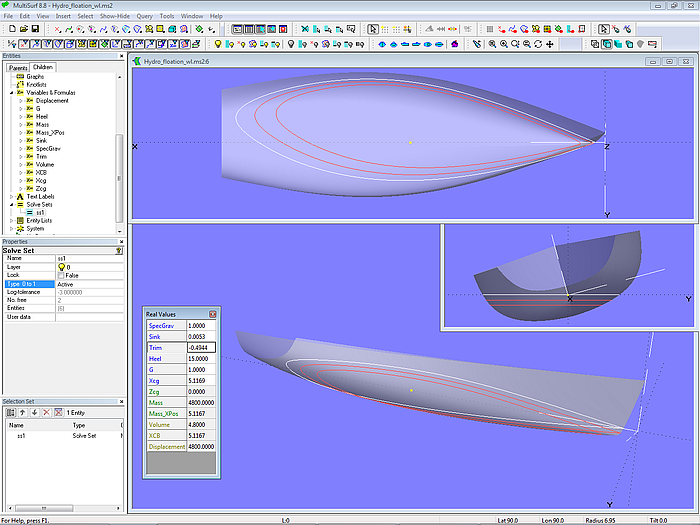
Modell Hydro_flotation.ms2 – freie Schwimmlage bei Krängung
So viel zum Thema, wie Hydrostatic Reals nützliche Informationen zum Rumpfentwurf beitragen.
Berechnung des Rumpfwiderstands
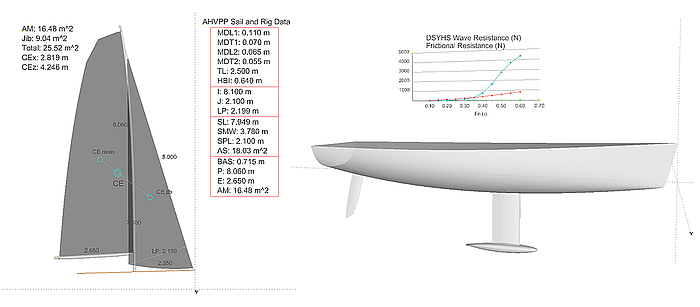
Mit Variablen und Formeln kann die Vorhersage hydrodynamischer Größen in einem Rumpfmodel im-plementiert werden. Für Segelboote gibt es beispielsweise die als Delft Systematic Yacht Hull Series (DSYHS) bekannten und berühmten Forschungsergebnisse.
Das Modell DSYHS.ms2 berechnet Wellenwiderstand und Reibungswiderstand gemäß den DSYHS-Gleichungen, die in dem Buch Aero-Hydrodynamics and the Performance of Sailing Yachts (Fabio Fossati; Adlard Coles Nautical, London, 2009) angegeben sind.
Der für die Wellenwiderstand angegebene Ausdruck lautet (Seite 24):
Rw LCB V^(2/3) BWL V^(1/3) LCB
----------- = a0 + ( a1 * ------- + a2 * Cp + a3 * ----------- + a4 * -------- ) * ----------- + ( a5 * -------- +
V * ρ * g LCF AWP LWL LWL LCF
BWL V^(1/3)
a6 * -------- + a7 *Cm ) * -----------
Tc LWL
mit
- Rw: Wellenwiderstand (N)
- LWL: theoretische Wasserlinienlänge (m)
- BWL: theoretische Wasserlinienbreite (m)
- Cp: Schärfegrad (prismatischer Koeffizient
- V: Rumpfvolumen (m^3)
- LCB: Abstand Volumenschwerpunkts vom vorderen Lot (m)
- LCF: Abstand des Wasserlinienflächenschwerpunkts vom vorderen Lot (m)
- AWP: Wasserlinienfläche (m^2)
- Tc: Rumpftiefgang (m)
- Cm: Völligkeitsgrad der Hauptspantfläche
- g: Erdbeschleunigung (m/s^2)
- ρ: Dichte des Wassers (kg/m^3)
- a0 ... a7: Koeffizienten in Abhängigkeit von der Froude-Zahl (Tabelle 2.5, Seite 24)
Als Formel für den Reibungswiderstand ist angegeben (Seite 14):
Rf = ½ * ρ * v^2 * Cf * AW
mit:
- Rf: Reibungswiderstand (N)
- ρ: Dichte des Wassers (kg/m^3)
- v: Bootsgeschwindigkeit (m/s)
- Cf: Widerstandsbeiwert
- AW: benetzte Oberfläche (m^2)
Der Beiwert des Reibungswiderstands ist gegeben durch:
0.075
Cf = ----------------------------------------------
(lg(588000 * LWL * v ) – 2) ^2
Er ist abgeleitet aus der ITTC 57-Formel unter Verwendung von 70% der Wasserlinienlänge für die Berechnung der Reynolds-Zahl.
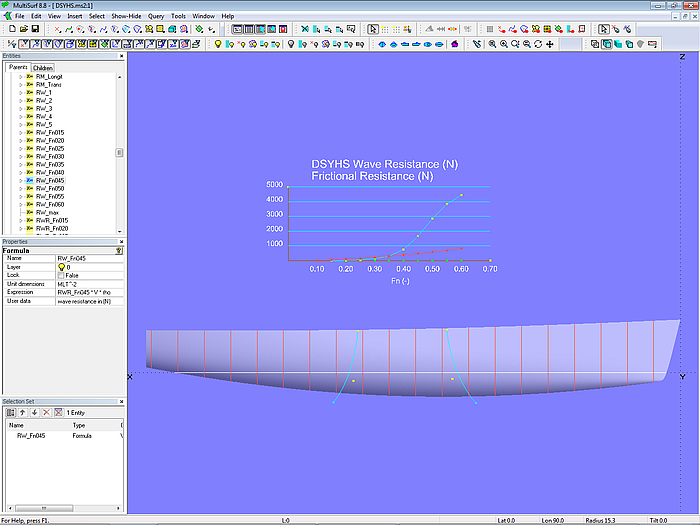
Modell DSYHS.ms2 – Wellenwiderstand und Reibungswiderstand berechnet nach den Gleichungen der Delft Systematic Yacht Hull Series
Die erforderlichen hydrostatischen Werte für die Berechnung der Formeln werden auf die oben erklärte Weise mit Hydrostatic Reals ermittelt. Der Wellenwiderstand wird für 10 Froude-Zahlen im Bereich von 0,15 bis 0,60 mit den jeweiligen Koeffizienten a0 – a7 berechnet. Für Bootsgeschwindigkeiten entsprechend diesen Froude-Zahlen wird der Reibungswiderstand bestimmt.
Über die Entity Lists frictional_resistance, wave resistance und velocities können die entsprechenden Zahlenwerte angezeigt werden – dazu Entity List auswählen, dann Taste „V“ drücken oder Hauptmenü/ Tools/ Real Values auswählen.
In einem Diagramm werden die Ergebnisse dargestellt. Zum Vergleichen, wie sich Änderungen der Rumpfform auswirken, kann man über das Kommando „Tempcopy“ den aktuellen Kurvenverlauf als tem-poräres 3DA-Wireframe-Objekt speichern (Taste „W“ oder Hauptmenü/ Tools/ Commmand Window). Diese können auch als permanente 3DA-Wireframes gespeichert werden.
Anordnung der Planken einer klassischen Yacht
Der Verlauf der Planken bei einem klassischen Bootsrumpf muß harmonisch sein, er muß dem Auge gefallen. Um dies zu erreichen, gilt der Grundsatz: alle Planken zwischen Schergang und erster Kielplanke sollen am gleichen Mall die gleiche Breite aufweisen. Im Folgenden wird gezeigt, wie man an Hand dieser Regel in MultiSurf den Plankenverlauf festlegen kann.
Rumpf
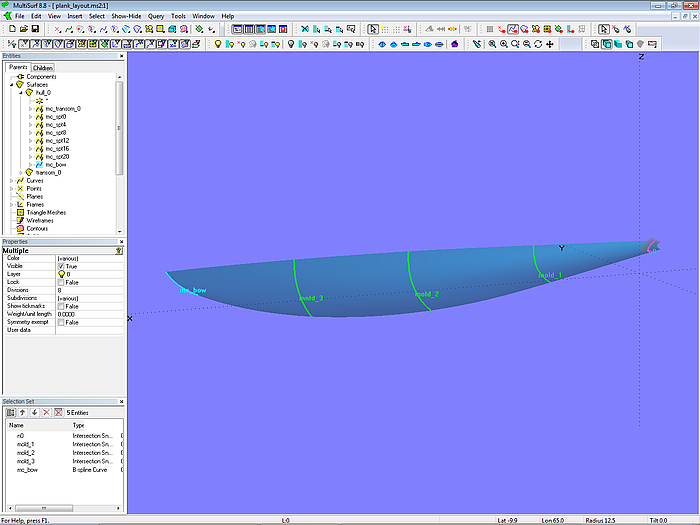
Als Beispiel dient das Modell plank_layout-1.ms2. Es enthält nur jene Flächen, Kurven und Punkte, die für die Erklärung der Plankenanordnung bei einem hölzernen Bootsrumpf notwendig sind.
Der Rumpf ist eine einfache -C-spline Lofted Surface, gestützt von B-spline-Mastercurves.
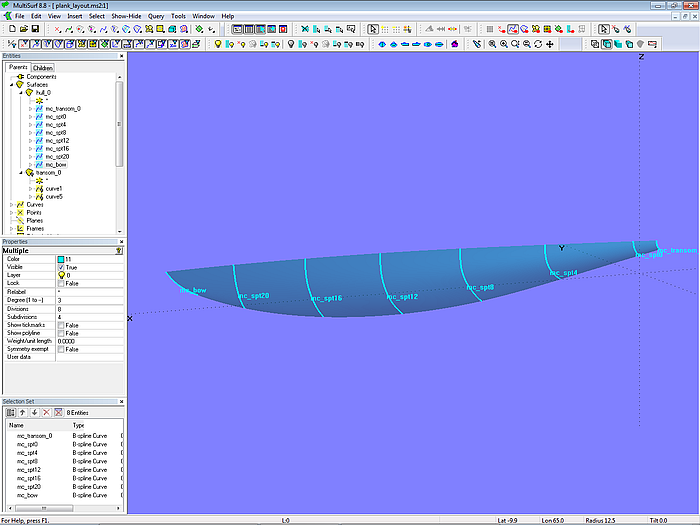
Modell plank_layout-1.ms2 - B-spline Mastercurves stützen die C-spline Lofted Surface
Warum so einfach?
Warum gibt es keinen Kiel?
Warum enden die Planken am Vorsteven und am Heckbalken, und nicht an den Sponungskurven?
Dies ist ein Beispiel. Je mehr Details, umso komplexer das Modell, die Darstellung auf dem Bildschirm, und folglich umso schwerer das Verständnis.
Der Verlauf der Planken wird in zwei Schritten definiert. Zuerst werden C-spline Curves für die Plankenkanten oder –nähte erzeugt. Diese Kurven werden dann mit Projected Snakes auf den Rumpf projiziert. Auf diese Weise hat der Verlauf der u-v-Parameterkurven der Rumpffläche keinen Einfluß auf den Verlauf der Plankenkanten, wie es der Fall wäre, wenn man mit C-spline oder B-spline Snakes den Plankenverlauf festlegen würde.
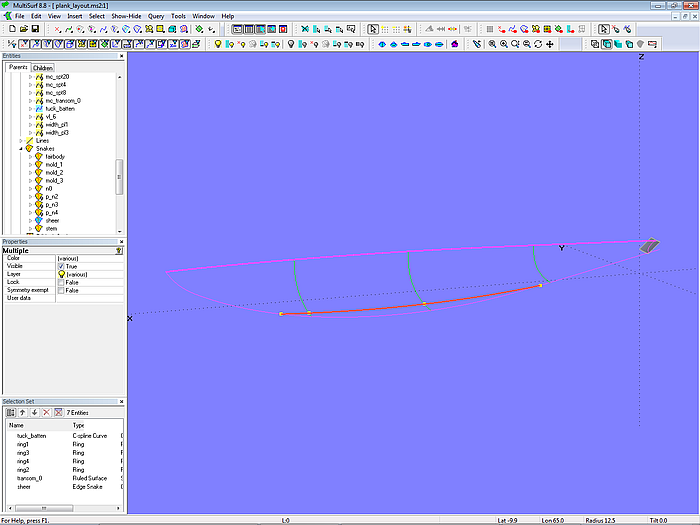
Mallen für die Definition der Plankennähte
Die Nahtkurven enden vorne entlang dem Vorsteven und achten am Spiegel oder am Heckbalken, dazwischen verbinden sie auf Mallen liegende Punkte auf dem Rumpf.
Warum hier nur 3 Mallen? (Bei einem 75 m^2-Schärenkreuzer wurden 10 Spantmallen verwendet.)
Dies ist ein Beispiel. Je mehr Mallen, umso mehr Dinge müssen beachtet werden. Das Ziel hier ist es, die Grundidee verständlich zu machen.
Modell plank_layout-1.ms2 – Mallen für die Kontrollpunkte der Plankennahtkurven
Die Grenze zwischen den Planken der Rumpfseite und den Planken der Kielseite
In diesem Beispiel geht es nur um den Bereich zwischen Schergang und der ersten Kielplanke. Die Oberkante dieser Planke bildet die Grenze zwischen den Planken der Rumpfseite und den Planken der Kielseite. Diese Grenzkurve beginnt dort, wo der Rudersteven den Heckbalken berührt, sie endet am Vorsteven. Sie ist eine geodätische Kurve auf dem Rumpf, das heißt, der kürzeste Weg auf der Oberfläche. Sie verläuft wie eine dünne Leine, die zwischen ihren Endpunkten am Rumpf festgespannt ist.
Modell plank_layout-1.ms2 – Bereich der Beplankung zwischen Schergang und erster Kielplanke
Plankenverlauf - Grundregel
Die Grundregel für den Verlauf der Beplankung (oberhalb der Kielplanken) lautet: alle Planken haben am gleichen Mall die gleiche Breite.
Daher müssen wir an jedem Mall die Kurvenlänge (Gurtmaß) von seinem oberen Ende bis zur Grenzkurve messen. Und dieses Maß dann durch die Anzahl der Planken teilen. Das Gurtmaß läßt sich über Hauptmenü/ Tools/ Measure/ Distance (oder die entsprechende Schaltfläche in der Werkzeugleiste) einfach bestimmen.
Betrachten wir zum Beispiel das Mall mold_2. Wählt man Ring ring6 (oberes Ende) und Ring ring4 (Schnittpunkt mit der Grenzkurve) aus und dann Tools/ Measure/ Distance, wird in den „Distance Mode“ gewechselt und es erscheint ein Distanz-Anzeigefenster. Da die Messung für zwei Ringe auf der gleichen Snake erfolgt, wird auch die Kurvenlänge zwischen diesen Punkten angegeben.
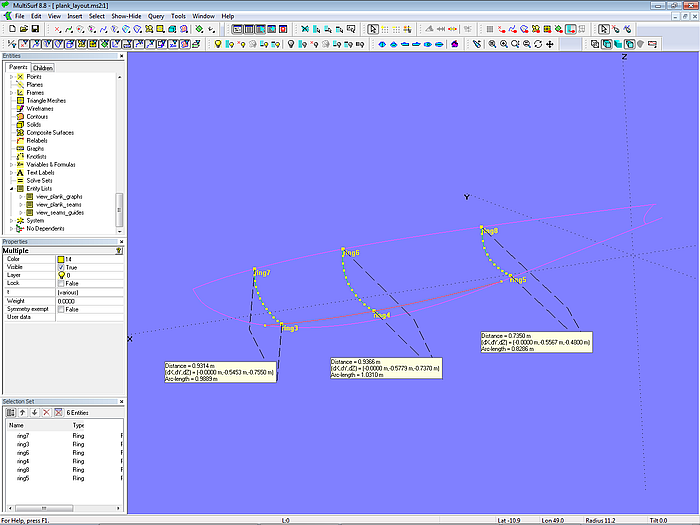
Modell plank_layout-1.ms2 – Distanzanzeige für die Kurvenlänge an 3 Mallen
An Mall mold_2 beträgt die Kurvenlänge 1,07 m. Bei 11 Planken von gleicher Breite ist an diesem Mall jede 0,097 m breit. Folglich sind auf Mall mold_2 10 Arc-length Rings zu setzen, jeweils Im Abstand von 0,097 m vom vorangehenden Ring entfernt.
Bei Mall mold_3 beläuft sich die Kurvenlänge auf 1.008 m, so daß sich für 11 Planken eine Breite von 0,091 m ergibt.
Modell plank_layout-1.ms2 – Plankennähte, definiert mit Hilfe von Arc-length Rings auf Spiegel und Spantmallen
Diese Arc-length Rings auf den Spantmallen und dem Spiegel sind zusammen mit normalen Ringen entlang Vorsteven und Heckbalken die Kontrollpunkte für die Nahtkurven.
Man beachte die besondere Situation bei Mall mold_1. Die Grenze zwischen Rumpf- und Kielbeplankung liegt vor dieser Position. Mithin können nur 10 Planken gleicher Breite an diesem Mall angebracht werden. Der untere Ring (ring5) für die Gurtmessung muß so positioniert werden, daß die Nahtkurve (C-spline Curve c_n11) strakend verläuft. Da der Anfangspunkt dieser Nahtkurve (ring9 auf dem Heckbalken) nahe bei mold_1 liegt, muss auch dessen Lage sorgfältig gewählt werden, so daß die Nahtkurve c_n11 gut strakt.
Auch die Länge der Plankenenden, bestimmt durch die Endpunkte der Nahtkurven entlang Vorsteven und Heckbalken, muß sich auf harmonische Weise ändern. Ob alle Nahtkurven gut straken, läßt sich in der 3D-Ansicht gut kontrollieren. Man dreht das Modell auf dem Bildschirm so, daß man schräg entlang der Kurven schauen kann. Genau so, als hätte man ein echtes Modell gebaut und würde es in seiner Hand hin und her bewegen. Auf diese Weise läßt sich jede Unregelmäßigkeit im Verlauf der Kurven feststellen.
In unserem Beispiel wird angenommen, dass der Schergang nicht breiter ist als die nachfolgenden Planken. Wird ein breiterer Schergang gewünscht, um zum Beispiel die Abdeckung durch eine Scheuerleiste zu kompensieren, definiert man zuerst diese Planke und beginnt die Gurtmessungen entsprechend von ihrer Unterkante aus.
Wie gesagt, dies ist ein Beispiel. Je mehr Mallen, umso mehr Dinge sind zu beachten. Ziel ist, das Grundprinzip zu verstehen.
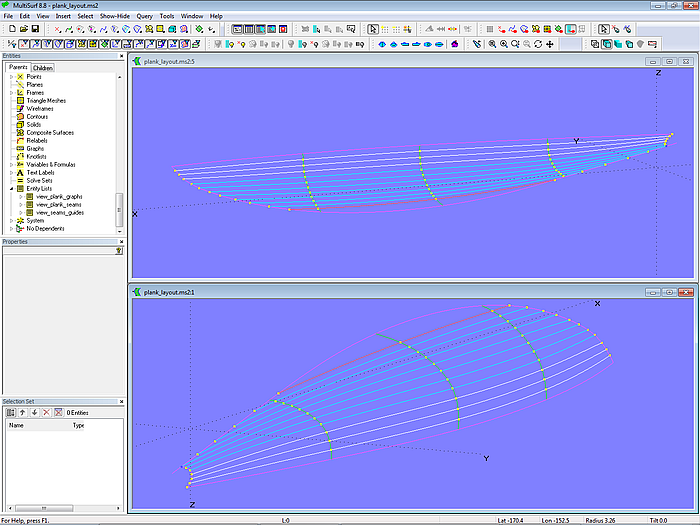
Plan der Plankenbreite
Um sicherzustellen, dass sich die Planken gleichmäßig verjüngen, ist eine Zeichnung der Plankenbreite hilfreich. Im Modell plank_layout-1.ms2 ist dies für Planke Nr. 1 und Nr. 3 gezeigt.
Die Entity List view_plank_graphs enthält alle Objekte, um den Verlauf der Breite über der Plankenlänge als Kurven darzustellen. Sie werden automatisch aktualisiert, wenn zugrundeliegende Objekte geändert werden. Die Konstruktion ist nicht so komplex, sie verwendet Copy Beads, Copy Curves und Intersection Beads, um die Breite bei 0, 20, 40, 60, 80 und 100 Prozent der Plankenlänge in ein Raster von Linien gleichen proportionalen Abstands zu übertragen.
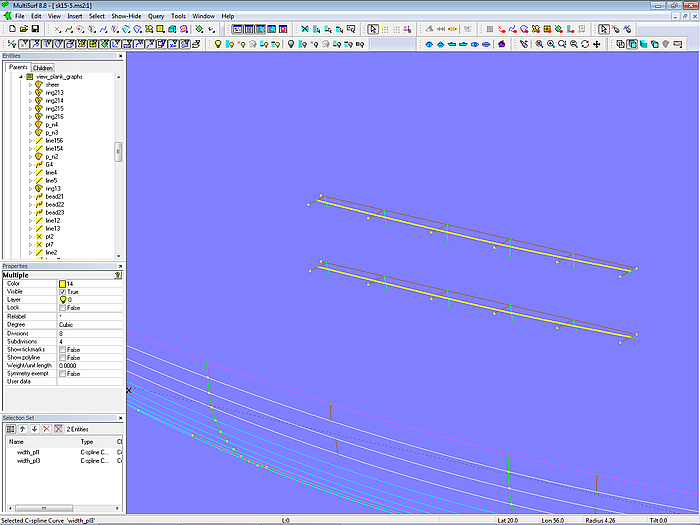
Modell plank_layout-1.ms2 – Kurven der Plankenbreite
Berechnung der Plankenbreite mit Variablen und Formeln
Das Modell kann erweitert werden, um langwieriges Bearbeiten zu vermeiden. Wenn zum Beispiel der Verlauf der Grenze zwischen dem Bereich der Beplankung von Rumpf und Kiel geändert wird, ändern sich auch die Gurtmaße an den Mallen. Aber es erfolgt keine automatische Anpassung der Plankenbreiten.
Im Modell plank_layout-2.ms2 geschieht dies mit Hilfe von Variablen und Formeln. Ändert sich das Gurtmaß an einem Mall, werden automatisch alle darauf liegende Arc-length Rings näher zusammen oder weiter auseinander geschoben. Gleiches erfolgt, wenn die Anzahl der Planken geändert wird.
Die Rechenausdrücke in den verwendeten Formeln sind einfach. Zum Beispiel gibt die Formel al_mold_1 die Kurvenlänge zwischen ring8 und ring5 auf Mall mold_1 zurück: al_mold_1 = ARCLEN (mold_1, TPOS (ring8), TPOS (ring5)).
Die Variable n_mold_1 gibt die Anzahl der Planken an Mall mold_1 an. Daher lautet der Ausdruck in der Formel d_mold_1 für die Plankenbreite bei mold_1: d_mold_1 = al_mold_1 / n_mold_1.
Was immer jetzt geändert wird am Rumpf, seine Form oder die Grenzkurve zwischen der Beplankung von Rumpf- und Kielseite, automatisch wird die Plankenbreite angepasst.
Da die Endpunkte der Plankennähte entlang Vorsteven und Heckbalken sich nicht mit ändern, muß der Strak, wie oben beschrieben, visuell kontrolliert werden.
Vermessungsregeln im Modell
Einführung
Der Entwurf einer Yacht in Übereinstimmung mit spezifischen Klassenvorschriften erfordert den permanenten Vergleich der Rumpfabmessungen mit Regelmaßen. Die Funktion "Distance Mode" (Hauptmenü/ Tools/ Measure/ Distance) bietet eine dynamische Anzeige der Entfernung zwischen zwei Punkten (auch der Kurvenlänge, falls die Punkte auf der gleichen Kurve oder Snake liegen). Eine Reihe von Distanzanzeigen läßt sich leicht erstellen, um Rumpfdaten anzuzeigen.
Distanzanzeigen sind jedoch bei jeder MultiSurf-Sitzung neu einzurichten, sie sind nicht dauerhaft in der Modelldatei gespeichert (und auch nicht in der Undo/ Redo-Sequenz enthalten). Oft erfordern Klassenre-geln weitere mathematische Operationen mit gemessenen Werten. Die Anwendung von Variablen und Formeln ist darum ein besserer Weg, um Vermessungdaten während der Entwurfsarbeit bereit zu stellen.
Der Einbau einer Vermessungsregel in ein MultiSurf-Modell wird hier an Hand der Klassenvorschriften für Schärenkreuzer gezeigt.
Schärenkreuzer – Vermessungsvorschrift
Grundlage der Rumpfvermessung ist eine Tabelle mit den Rumpfmaßen eines idealen Schärenkreuzers. Überschreiten bestimmte Abmessungen die Idealwerte, sind Deplacement, mittlere Breite, Freibord und Kiellänge zu erhöhen.
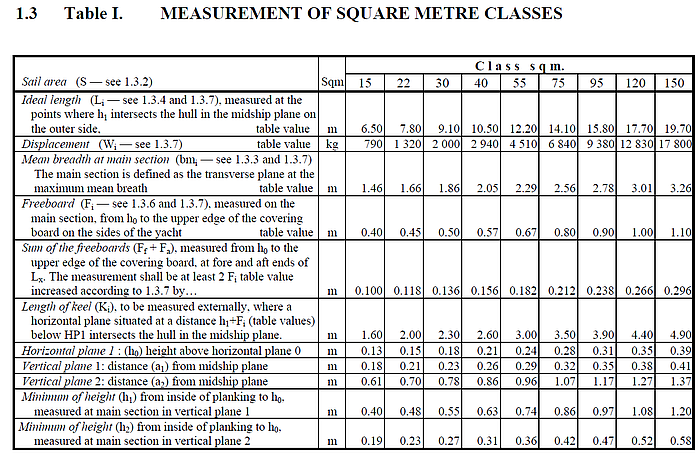
Tabelle 1: ideale Rumpfabmessungen (entnommen aus: “Rules for skerry cruisers (square metre yachts)”, SSKF, 2013)
Die Rumpfmasse werden in mehreren Horizontal- und Querebenen ermittelt.
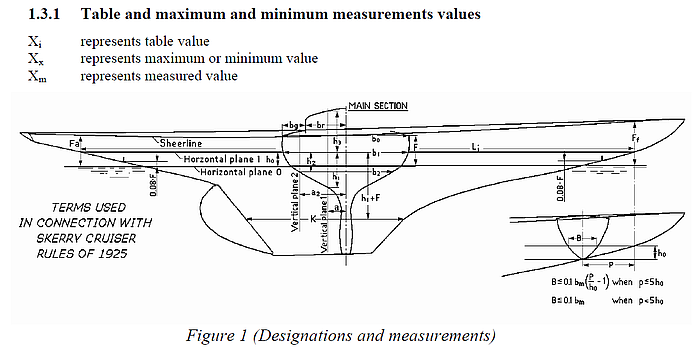
Definition der Messebenen in Horizontal- und Querrichtung (entnommen aus: “Rules for skerry cruisers (square metre yachts)”, SSKF, 2013)
Beispiel: 15 m^2-Schärenkreuzer
Als Beispiel betrachten wir das Rumpfmodell eines 15 m^2-Schärenkreuzers (sk15-1.ms2). Es ist nicht beabsichtigt, ein komplettes Modell mit Deck, Spiegel, Ruder, Aufbau usw. zu erstellen. Es geht auch nicht um eine Rumpfform mit bestimmten Proportionen, außer dass sie zu den Klassenregeln passt.
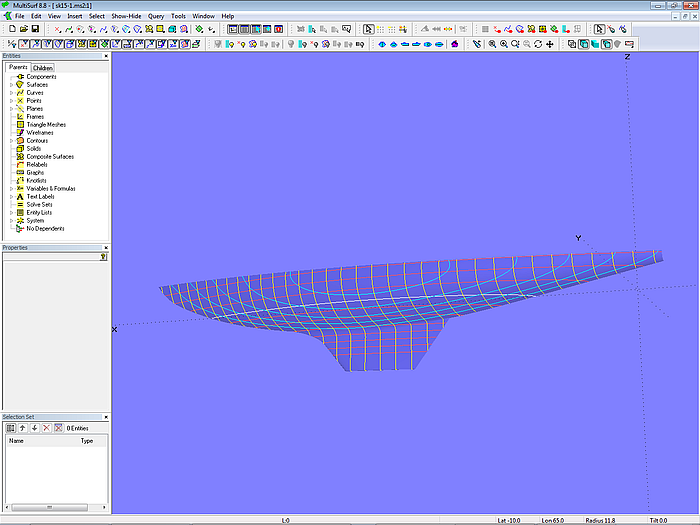
Modell sk15-1.ms2 – Rumpf eines 15 m^2-Schärenkreuzers
Der gesamte Bootsrumpf besteht aus 3 Flächen: C-spline Lofted Surface hull_0 (Rumpf), B-spline Lofted Surface keel_0 (Kiel) und Blend Surface keel_fillet (Übergang vom Rumpf zum Kiel).
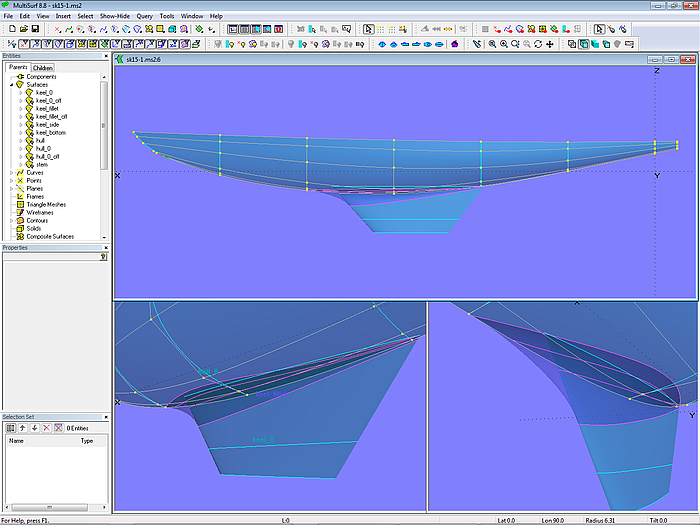
Modell sk15-1.ms2 – Rumpf, Kiel und Übergang
Der Rumpf wird mit 8 Mcs definiert, jede ist eine B-spline Curve vom Grad 3 mit 6 Cps. Vertexkurven (C-spline Curves, die korrespondierende Cps verbinden) dienen als Strakhilfe. Die Kielfläche wird durch 3 in Wasserlinienrichtung verlaufende B-splines Curves mit je 6 Cps erzeugt. Für die Kielausrundung werden B-spline Snakes verwendet, die jeweils mit 6 Magneten bestimmt werden.
Es gibt mehrere Entity-Lists. Wird eine ausgewählt, lassen sich mit der Schaltfläche „Show Parents“ in der Werkzeugleiste oder über Hauptmenü/ Show-Hide/ Show Parents alle ihre Mitglieder anzeigen. Zum Beispiel gibt es die Entity List edit_hull_0; sie enthält nur die Objekte, mit denen sich die Form des Rumpfes ändern läßt. Mit Entity Lists kann man sich schnell nur das anzeigen lassen, was man zur Bearbeitung gerade braucht. So läßt sich wirksam die Bildschirmanzeige kontrollieren.
Die Entity List measurements enthält die Vermessungsdaten. Die Anzeige erfolgt mit Text Labels. Die Gruppe "Table Values" zeigt die Daten gemäß Tabelle I an. Die Tabellenwerte werden durch Variablen definiert.
Die Gruppe "Measured Values" listet die an den verschiedenen Rumpfpositionen ermittelten Maße auf. Gegebenenfalls werden zur Berechnung Formeln verwendet.
Die Gruppe "Required Values" zeigt die vergrößerten Abmessungen an, falls die ideale Länge Li überschritten wird.
Für jede Datengruppe gibt es auch eine eigene Entity List. Somit kann man sie in separaten Fenstern anzeigen über Hauptmenü/ Tools/ Real Values oder die "V“-Taste.
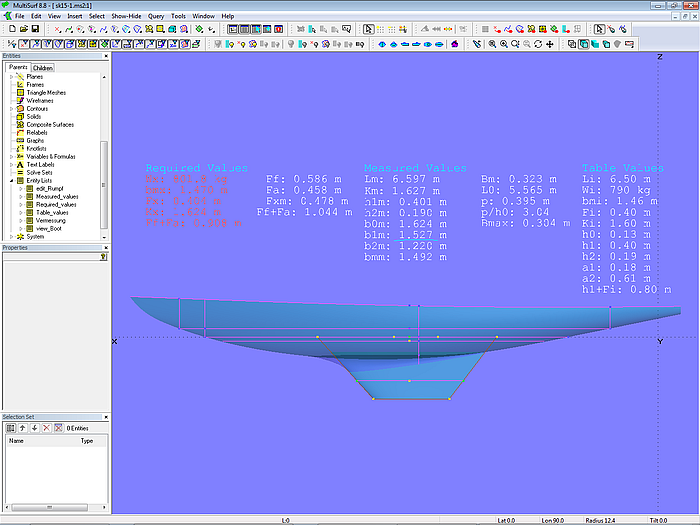
Modell sk15-1.ms2 – Vermessungsdaten und Messebenen
Wird die Form von Rumpf oder Kiel geändert, sind die Auswirkungen auf die Messwerte sofort ersichtlich.
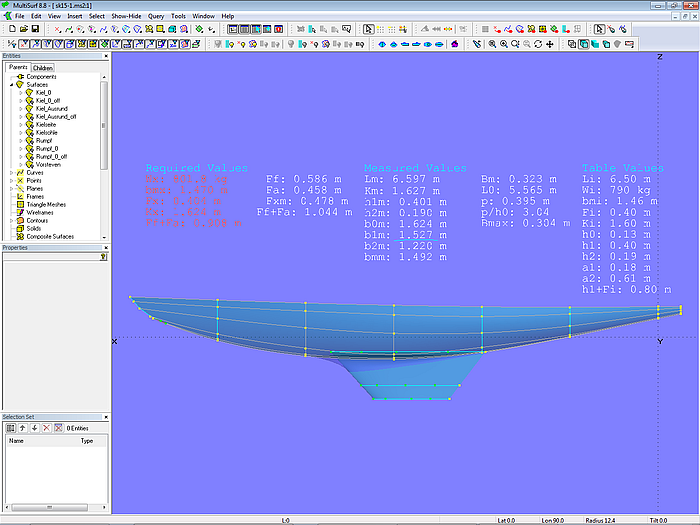
Modell sk15-1.ms2 - Vermessungsdaten und Masterkurven von Rumpf und Kiel
Verwendete Formeln
Die hier verwendeten Formeln sind einfach. Einige führen Berechnungen durch, aber die meisten bestimmen lediglich die XYZ-Position eines Punktes oder die Entfernung zwischen zwei Punkten.
Die in den Formeln verwendeten Funktionen XPOS, YPOS, ZPOS, TPOS geben die XYZ- und t-Position eines Punktes zurück. Zum Beispiel: der Freibord am Hauptspant soll berechnet werden. Am Anfang dieser Spantkurve liegt ring10; die Formel Fxm berechnet die Freibordhöhe dann mit dem Rechenausdruck: ZPOS (ring10).
Ein weiteres Beispiel: die Punkte ring11 und ring12 liegen am Anfang und am Ende der Wasserlinie. Die Wasserlinienlänge wird nun durch die Formel L0 unter Verwendung des Ausdrucks XPOS (Ring11) - XPOS (Ring12) berechnet.
Die Liste aller in MultiSurf zur Verfügung stehenden Funktionen, wie zum Beispiel ARCLEN (Bogenlänge zwischen zwei Kurvenpunkten), AREA (Größe einer Fläche), CENTROID (XYZ-Koordinaten des Flä-chenschwerpunkts), befindet sich am Ende dieses Tutorials.
Hauptspant
Die Bestimmung des Hauptspants verdient einen genauere Betrachtung. Die Klassenregeln definieren den Hauptspant als diejenige Querschiffsebene, für die die mittlere Breite bm am größten ist. Die Definition der mittleren Breite lautet: bm = (b0 + 4 x b1 + b2) / 6; b0, b1 und b2 sind Breitenmessungen: b0 an Seite Deck, b1 in Messebene plane1 und b2 in einer bestimmte Distanz unter dieser.
Um die Suche nach der maximalen mittleren Breite zu automatisieren, wird der Bead e0 auf der in der Mittschiffsebene liegenden Line l0 erzeugt. An der X-Position von e0 werden diese 3 Breitenmessungen mit Hilfe von XYZ-Ringen durchgeführt. Dann wird bm durch die Formel bm_i berechnet. Mit dieser Formel wird die Z-Position von Punkt pt15 definiert.
Nun wird die t-Position von e0 von 0 bis 1 geändert und der Pfad von pt15 über die Procedural Curve c0 aufgezeichnet. Die maximale Z-Höhe dieser Kurve wird durch den Proximity Bead e1 gefunden. Seine X-Position ist die gesuchte Lage des Hauptspants.

Modell sk15-1.ms2 - Bestimmung des Hauptspants nach den Vermessungsregeln der Schärenkreuzer-Klasse
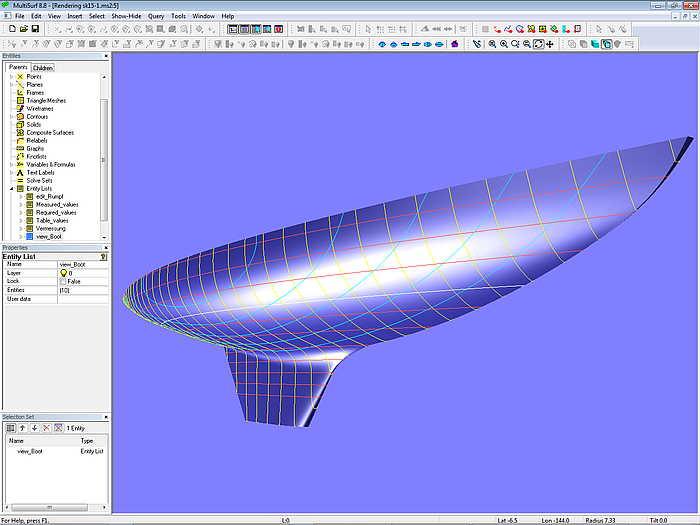
Modell sk15-1.ms2 - 15 m^2-Schärenkreuzer-Rumpf
Mathematische Funktionen in MultiSurf
| Name | Argument(s) | Result | Synopsis |
| ABS | 1, any units | Same units as argument | Absolute value |
| ACOS | 1: unitless | unitless | arc cosine (radians) |
| ACOSD | 1: unitless | unitless | arc cosine (degrees) |
| ALARM | 2: any units | Unitless | ALARM has 2 arguments ALARM(x,y). The alarm "goes off" (goes into error) if (1) it is set (x > 0) AND (2) y < 0. Using a formula or expression for y, you can build various warning limits into a model. |
| ANGLE | 3: point, point, point | Unitless (degree) | Angle of three points (angle at pt2 between the directions to pt1 and pt3) |
| ARCLEN | 3: curve, unitless, unitless | Length | Arc distance along curve, from t1 to t2 |
| AREA | 2: surface, use_sym (0 or 1) | Area = L^2 | Area of surface, CompSurf, or TriMesh |
| ASIN | 1: unitless | unitless | arc sine (radians) |
| ASIND | 1: unitless | unitless | arc sine (degrees) |
| ATN | 1, unitless | Radian (unitless) | Arc tangent |
| ATND | 1, unitless | Degree (unitless) | Arc tangent (in degrees) |
| ATN2 | 2, both with same units | Radian (unitless) | Arc tangent(y/x) |
| ATN2D | 2, both with same units | Degree (unitless) | Arc tangent(y/x) (in degrees) |
| BBOX | 1. Entity or Entity List 2. Real scale factor 3. Real sign 4. Index, 1 to 3 for X, Y, or Z component | Length | The BBOX function gets information about the bounding box of an entity, or a set of entities specified by an Entity List. A bounding box is the smallest rectangular solid, aligned with the global coordinate system, that encloses the selected entities. |
| BSPL | 1. KnotList, or *UNIFORM for uniformly spaced knots. 2. K, polynomial order (2 for linear, 3 for quad-ratic, 4 for cubic, etc.) 3. N, number of basis functions. 4. I, index indicating which basis function to evaluate (1 to N). 5. T, parameter (nominal range 0 to 1, but can be any real value) |
unitless | The BSPL function evaluates the so-called “B-spline basis functions”, which are the mathematical foundations of B-spline and NURBS curves and surfaces. Example: BSPL( *UNIFORM, 3, 5, 2, 0.40) returns 0.3200. In this case the knots are uniform (0, 0, 0, 1/3, 2/3, 1, 1, 1); the B-splines are quadratic (K = 3); there are N = 5 of them; I = 2 selects the second basis function; T is 0.40. Errors: 222. NURB has too few knots for its order and num-ber of control points. 223. NURB has too many knots for its order and number of control points. 234. Insufficient spacing between knots. 556. BSPL function: order less than 1. 557. BSPL function: number of basis functions less than 1. 558. BSPL function: index is out of range (1 to num-ber of basis functions). |
| CEIL | 1: any units | Same units as argument | CEIL(x) is the smallest integer that is greater than or equal to x. |
| CENTROID | 3: entity, use_sym (0 or 1), index (1-3, for X,Y,Z coordinate) | Length | Coordinates of centroid |
| CLEAR | 2: point, graphic entity | Length | Clearance |
| COS | 1, radian (unitless) | Unitless | Cosine |
| COSD | 1, degree (unitless) | Unitless | Cosine (of angle in degrees) |
| COSH | 1: unitless | unitless | hyperbolic cosine |
| CURV | 1/Length | Curvature of host curve or snake, at t location of bead/ring. If t is on a breakpoint, hi_side (0 or 1) controls whether curvature is measured below or above the break. kind: 0 is 3-D curvature of curve or snake; 1 is nor-mal curvature of snake; 2 is geodesic curvature of snake. |
|
| CURVINT | 3: curve, t, real | L times units of real | Integral of real times ds along curve. ds is the element of arc length along the curve. t is a Variable. real is a Formula descended from t. |
| DIST | 2: point, point | Length | Distance between points |
| ERROR | 1: entity | Unitless | Error code attached to entity (0 if no error). |
| EXP | 1, unitless | Unitless | Exponential |
| FLOOR | 1: any units | Same units as argument | FLOOR(x) is the greatest integer that is less than or equal to x. |
| FRAMEPOS | 3: point, frame, index (1-3, for x,y,z coordinate) | Length | Coordinates of point in frame |
| GRAPH | 2: graph, unitless | Unitless | Evaluation of graph |
| HYDRO | 6: sp.gr., Zcg, sink, trim, heel, index | various, depending on index | Fixed-position hydrostatics based on the visible contours. index is 1 to 29; selects one of 29 results, e.g. index = 6 for displacement volume; index = 15 for wetted surface. |
| IF | 3: any units | Same as units of selected argument | If arg1 >0, arg2; else arg3 |
| LOG | 1, unitless | Unitless | Natural logarithm |
| LOG10 | 1, unitless | Unitless | Base-10 logarithm |
| MASS | 3: entity, use_sym, index | M ML |
Mass, if use_sym is not 0, includes symmetry images. Index = 0 returns Mass. Index = 1, 2 or 3, the value returned is the mass moment with respect to X, Y or Z. This is the product of mass times the X, Y or Z coordinate of the centroid. Unit dimensions are ML. |
| MAX | 2, both with same any units | Same units as arguments | Maximum |
| MIN | 2, both with same any units | Same units as arguments | Minimum |
| PI | 1; any units | Unitless | PI has 1 argument, but its value is immaterial; PI(x) = pi for any x. |
| ROUND | 1, any units | Same units as argument | Rounding to integer |
| ROUND2 | 1, any units | Same units as argument | ( x, places) rounds x to the specified number of decimal places. E.g., ROUND2(PI(0),2) is 3.140000. |
| SIGN | 1: any units | Unitless | SIGN(x) is +1 when x > 0, -1 when x < 0, 0 when x = 0. |
| SIN | 1, radian (unitless) | Unitless | Sine |
| SIND | 1, degree (unitless) | Unitless | Sine (of angle in degrees) |
| SINH | 1: unitless | unitless | hyperbolic sine |
| SQRT | 1, unit dimensions all multiples of 2 | Unit dimensions of argument divided by 2 | Square root |
| STRAIN | 2: Surface/TriMesh, index | Unitless | Surface/TriMesh is a surface or TriMesh entity index = 0 or 1, for minimum or maximum strain This function reports the strain range for an Expanded Surface or Expanded TriMesh. |
| SURFCURV | 5: magnet, hi_side_u, hi_side_v, kind, angle | L^-1 for kind = 0 or 2; L^-2 for kind = 1 | Surface curvature kind = 0, normal curvature kind = 1, Gaussian curvature kind = 2, mean curvature |
| SURFINT | 4: surface, u, v, real | L^2 times units of real | Integral of real times dA over surface dA is the element of area on the surface u and v are Variables real is a Formula descended from u and v. |
| TAN | 1, radian (unitless) | Unitless | Tangent |
| TAND | 1, degree (unitless) | Unitless | Tangent (of angle in degrees) |
| TANH | 1: unitless | unitless | Hyperbolic tangent |
| TPOS | 1, bead or ring | Unitless | t parameter |
| UNITMASS | 1: entity | M for a point ML^-1 for a curve ML^-2 for a surface ML^-3 for a solid |
unit weight property of entity |
| UPOS | 1, magnet or ring | Unitless | u parameter |
| VELOCITY | 3: curve, t, hi_side | Length | Rate of change of arc length with respect to t If t is on a breakpoint, hi_side (0 or 1) controls whether velocity is measured below or above the break. |
| VOLUME | 2: solid, use_sym (0 or 1) | Volume = L^3 | Volume of solid |
| VPOS | 1, magnet or ring | Unitless | v parameter |
| XPOS | 1, point | Length | X coordinate |
| YPOS | 1, point | Length | Y coordinate |
| ZPOS | 1, point | Length | Z coordinate |
======================================================================================