Automatische Variation der Rumpfform
Abgeleitete Masterkurven für Sollwerte von Volumen und LCB
von Reinhard Siegel
Inhalt
Einleitung
1 Basis-Rumpf
2 Abgeleitete Masterkurven - Grundprinzip
3 Abgeleiteter Rumpf
4 Änderung der Querverschiebung über der Rumpflänge
5 Automatische Anpassung der abgeleiteten Mcs für Sollwerte von Volumen und LCB
6 Export der abgeleiteten Rumpfform
7 Import eines Basis-Rumpfes
Anhang 1 - on systematic variation of hull forms: the Lackenby method
Anhang 2 - on automated adjustment of hull form: mastercurve relocation
Einleitung
Der Entwurf einer Rumpfform ist ein iterativer Prozess. Dieser Prozess muß konvergieren. Die iterativen Schritte müssen also kleiner und kleiner werden, die Rumpfformen werden immer ähnlicher. Unweigerlich wird der Punkt erreicht, wo die Form den Vorstellungen entspricht, nur das Verdrängungsvolumen könnte ein wenig größer sein, und es wäre schon schön, wenn das LCB auch noch ein paar Zentimeter achterlicher wäre, ansonsten passt alles. Aber dieser vermeintlich kurze Weg zum wirklich finalen Modell kann langwierig sein – die Kontrollpunkte der Masterkurven müssen dann hier und da nur um wenige Milimeter verschoben werden, und neben den Hydrostatikwerten muß auch der Strak dauernd überprüft werden. Diese Feinarbeit ist zeitraubend.
Der im Folgenden beschriebene Ansatz ermöglicht es, aus den Masterkurven eines vorhandenen Rumpfes automatisch neue Masterkurven zu generieren, so dass Sollwerte von Volumen und LCB erreicht werden. Dabei bleiben der Strak, die Außenkonturen des Rumpfes und der Formcharakter der Mcs erhalten.
Dieses Tutorium wurde angeregt durch die Beschäftigung mit dem Verfahren von H: Lackenby, über das im Anhang berichtet wird.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point); synonym verwendet
Mc: Masterkurve, Stützkurve (master curve, support curve); synonym verwendet
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
1 Basis-Rumpf
Ausgangspunkt ist das Modell eines Rumpfes, dass im Grunde fertig ist. Prominenten Kurven wie Seite Deck, Bodenkontur, Vorsteven, Spantverlauf – alles strakt und sieht aus wie vorstellt. Wäre da nicht der Wunsch, dass das Verdrängungsvolumen auf der Konstruktionswasserlinie etwas größer oder kleiner sein könnte, und Verdrängungsschwerpunkt LCB ein wenig vorlicher oder achterlicher liegen.
Also beginnt man, an den Kontrollpunkten der die Fläche stützenden Masterkurven herumzuschieben, stets im Blick den Strak und die Hydrostatikwerte. Braucht man etwas mehr Volumen, werden die Mcs so geändert, dass die Spanten völliger werden. Soll LCB nach achtern, macht man sie vorne etwas schlanker, achtern etwas bauchiger. Wie dieses Editieren der Form der Mcs automatisiert werden kann, wird im Folgenden beschrieben.
Modell model-0.ms2 zeigt den Basis-Rumpf, eine C-spline Lofted Surface, gestützt von 6 B-spline-Masterkurven, jede kontrolliert mit 6 Punkten.
Wir gehen im Weiteren also davon aus, dass bis auf Volumen und/oder LCB der Rumpf im Grunde fertig ist. Die Aufgabe besteht mithin darin, die Form der inneren Mcs so zu ändern, dass bestimmte Werte für Volumen und LCB erreicht werden. Wobei der Charakter des Kurvenverlaufs der Mcs aber beibehalten werden soll - aus einer U-Spantform soll keine V-Spantform werden.
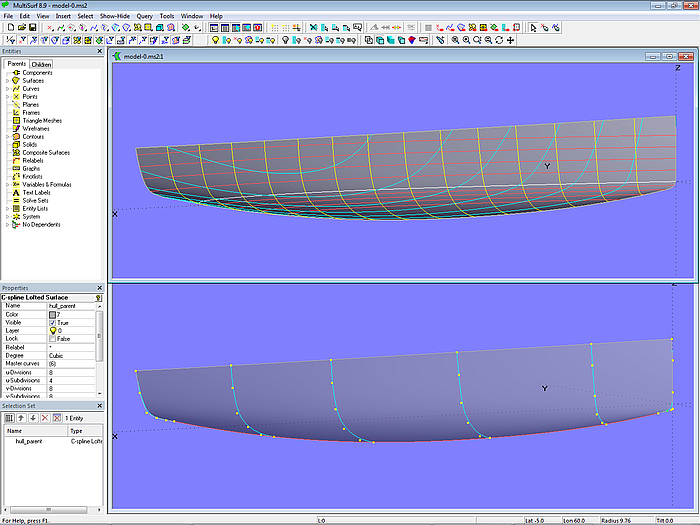
Modell model-0.ms2 – der Basis-Rumpf ist eine C-spline Lofted Surface mit 6 B-spline Masterkurven.
2 Abgeleitete Masterkurven – Grundprinzip
Um eine Mc etwas völliger oder schlanker zu machen, ohne dabei den Character ihrer Form zu verändern, müssen die inneren Cps sowohl vertikal als auch horizontal verschoben werden. Diese Erfahrung aus der Praxis führt zu dem Ansatz, der im Modell model-1.ms2 anhand mc4 beschrieben wird. Es wird eine abgeleitete Mc konstruiert, indem zu jedem inneren Cp der Basis-Mc ein neuer Cp erzeugt wird. Dieser abgeleitete Cp liegt auf der Halbierenden des Winkels zwischen seinen angrenzenden Polygon-segmenten, und ist um eine bestimmte Distanz zum Basis-Cp versetzt.
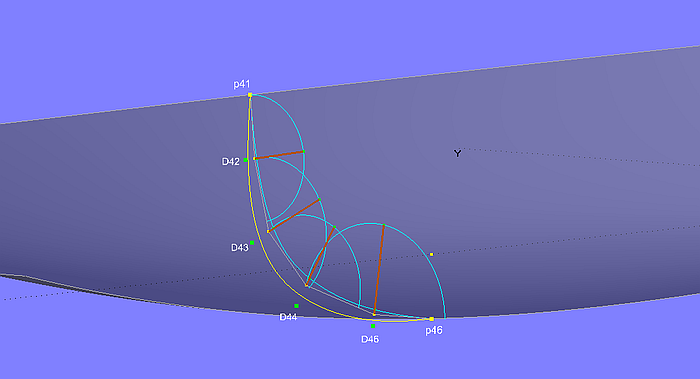
Modell model-1.ms2 – Basis-Mc und davon abgeleitete Kurve
Zunächst wird die Winkelhalbierende des Winkels zwischen cp1, cp2 und cp3 bestimmt. Dazu wird der Arc curve_42 (Type 2) mit den Punkten p41, p42 und p43 erzeugt. Auf dem Kreisbogen curve_42 liegt der Bead bead_42. Da sein Parameterwert auf t = 0.5 gesetzt ist, ist die Linie line_42, die p42 mit bead_42 verbindet, die Winkelhalbierende. Auf line_42 liegt der Arc-length Bead D42.
Diese Konstruktionsschritte werden dann mit den Cps (p42, p43, p44), (p43, p44, p45) und (p44, p45, p46) wiederholt.
Ergebnis sind die 4 Arc-length Beads D42, D43, D44 und D45, die jeweils auf den Winkelhalbierenden des Kontrollpunkt-Polygons von mc4 liegen. Auf diese Weise besteht ein enger Zusammenhang zwischen der Anordnung der Cps von Basis-Mc und abgeleiteter Mc.
Die Linien, auf denen die neuen Cps liegen, sind nun bekannt. In welcher Distanz d zu den Basis-Cps sie versetzt sind, steht aber noch nicht fest. Darum wird ein Maximalwert der Abweichung (Verschiebung) von der Basis-Mc definiert, und dieser so entlang der Basis-Mc verteilt, dass die abgeleitete Kurve ohne Verschiebung bei Cp1 (p41) beginnt, ohne Verschiebung am letzten Cp (p46) endet und dazwischen die gegebene Maximalabweichung erreicht.
Als Verschiebungsfunktion wird folgender Ausdruck verwendet:
d = c x (t –t^2)
Hierbei ist c eine Konstante und t der Parameterwert desjenigen Kurvenpunktes auf der Basis-Mc, in dem diese von der Winkelhalbierenden geschnitten wird.
Es ist ersichtlich, dass für t = 0 und t = 1 die Verschiebungsfunktion d den Wert Null annimmt.
Um die Konstante c zu bestimmen, wird angenommen, dass für t = 0.5 der Maximalwert der Verschiebung d gleich dem Wert n sein soll. Damit ergibt sich die Funktion d zu:
d = n x 4 x (t – t^2)
Dieser Ansatz ist in Modell model-1.ms2 mit Hilfe weniger Variablen und Formeln umgesetzt.

Modell model-1.ms2 – die Variable n4 kontrolliert, wie stark die abgeleitete Kurve von der Basis-Kurve abweicht.
Zunächst werden die Schnittpunkte von mc4 mit den Winkelhalbierenden (line_42, line_43, line_44 und line_45) durch die Intersection Beads e42, e43, e44 und e45 bestimmt. Die Variable n4 definiert die maximale Verschiebung.
Damit kann die Distanz d der einzelnen abgeleiteten Cps von den Basis-Cps berechnet werden. Zum Beispiel gehört zu Cp2 (p42) der Basis-Mc der abgeleitete Cp D42 (Arc-length Bead). Sein Abstand von p42 wird mit der Formel d42 und folgendem Ausdruck berechnet (die Funktion TPOS (e42) gibt den t-Parameterwert des Beads e42 zurück):
d42 = n4 x 4 x (TPOS (e42) - (TPOS (e42) )^2 )
Dieser Formelwert d42 wird nun in der Definition des Arc-length Beads D42 für die Größe „Arc dist“ ein-gesetzt.
Analog wird mit den Formeln d43, d44 und d45 der Abstand der übrigen Arc-length Beads (D43, D44, D45) von ihren Basis-Cps berechnet und für „Arc dist“ verwendet.
Verbleibt abschließend noch die Erzeugung der abgeleiteten Masterkurve mc4_derived mit diesen Kontrollpunkten: p41, D42, D43, D44, D45 und p46.
Ändert man den Wert der Variablen n4, ändert sich die Abweichung der abgeleiteten Kurve von ihrer Basis-Kurve. Nimmt n4 einen großen Wert an, kann gemäß der Verteilungsfunktion der vorletzte Cp (D45) so weit nach außen verschoben werden, dass seine Z-Koordinate kleiner ist als die des letzten Cps (p46), der auf der Mittschiffsebene liegt (dy = 0). Da dann die abgeleitete Kurve von schräg unten gegen die Mittschiffsebene läuft, würde ein negativer First zwischen beiden Rumpfhälften entstehen. Darum sorgt eine bedingte Verzeigung dafür, dass D45 nicht tiefer liegt als p46. Diese Bedingung ist in model-3.ms2 und model-4.ms2 mit Hilfe der IF-Funktion eingebaut.
3 Abgeleiteter Rumpf
In Modell model-2.ms2 ist diese Konstruktion der abgeleiteten Mc für die anderen inneren Mcs mc2, mc3 und mc5 in analoger Weise wiederholt. Man beachtete, dass die erste und letzte Mc (mc1, mc6) nicht verschoben werden.
Mit mc1, den 4 abgeleiteten Mcs und mc6 wird nun die C-spline Lofted Surface hull_derived erzeugt. Die Contours stations_derived, buttocks_derived, wl_above_derived, wl_below_derived und dwl_derived zeigen die Linien der abgeleiteten Rumpfform.
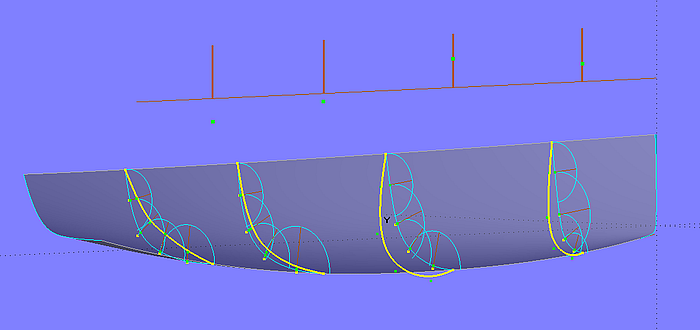
Modell model-2.ms2 – abgeleitete Masterkurven
Im Gegensatz zu model-1.ms2 wird die maximale Verschiebung n der inneren Mcs hier nicht duch Variablen definiert. Statt dessen werden die Werte n2, n3, n4, n5 mit Hilfe einer Art „Schieberegler“ bestimmt. Beispielsweise befindet sich an der Längsposition von mc4 die senkrechte Linie line4 und auf dieser der Bead bead7. Der Wert n4 ist der Abstand von bead7 vom Anfangspunkt der Linie (XYZBead bead3) und ergibt sich aus dieser einfachen Formel (die Funktion ZPOS gibt die Z-Koordinate eines Punktes zurück):
n4 = ZPOS(bead7) - ZPOS(bead3)
Versetzt man einen dieser „Schieberegler“-Beads, ändert sich die Verschiebung der abgeleiteten Mc.
Die „Schieberegler“-Beads sind unabhängig voneinander. Es ist offensichtlich, dass zwischen ihrer Position ein Zusammenhang bestehen muß, damit sich die Abweichung der abgeleiteten Mcs von den Basis-Mcs in Längsrichtung harmonsich ändert.
4 Änderung der Querverschiebung über der Rumpflänge
Wie sich diese Forderung umsetzen läßt, ist in Modell model-3.ms2 gezeigt. Die B-spline Curve curve_x bestimmt, wie die Stärke der Verschiebung der abgeleiteten Mcs in Längsrichtung variert. Diese Verschiebungskurve, die auf Mitte Schiff und relativ zur Linie line1 verläuft, hat nur 4 Cps. Mit 2 inneren Cps wird einen Wendepunkt im Verlauf von curve_x möglich. Auf diese Weise kann man zum Beispiel die abgeleiteten Mcs im Vorschiff etwas schlanker und im Hinterschiff etwas völliger machen als die Basis-Mcs.
Man beachte, dass der Verlauf von curve_x durch die beiden Beads bead3 und bead4 kontrolliert wird, die auf den horizontalen Linien links über dem Bug liegen („Schieberegler“). Versetzt man diese Punkte, ändert sich die Verschiebungskurve curve_x entsprechend.
Um am Ort einer der inneren Mc die maximale Verschiebung n zu bestimmen, wird line1 und curve_x an der X-Position der Mc geschnitten. Der Abstand zwischen dem Schnittpunkt auf line1 und dem Schnittpunkt auf curve_x ist die gesuchte maximale Verschiebung am Ort der Mc. Zum Beispiel lautet der Rechenausdruck der Formel n3 für die abgeleitete Mc3:
n3 = ZPOS (bead8) – ZPOS (bead7)
Hierbei ist bead8 der Schnittpunkt auf der Verschiebungskurve, bead7 der Schnittpunkt auf der Bezugslinie line1.
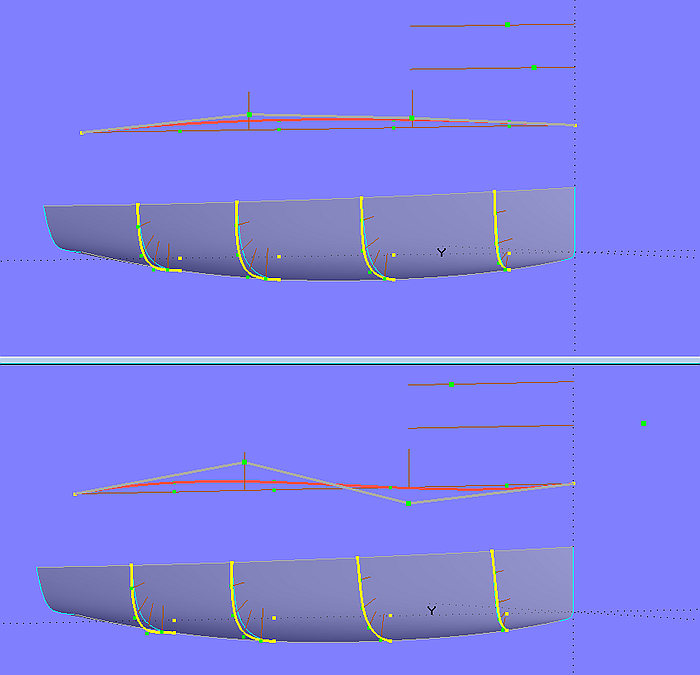
Modell model-3.ms2 – Änderung der Querverschiebung der abgeleiteten Mcs über der Rumpflänge
Da die Verschiebungskurve curve_x strakt, stehen auch die Abweichungen der abgeleiteten Mcs von ihren Basis-Mcs in einem harmonischen Verhältnis. Folglich strakt auch die abgeleitete Rumpfform.

Modell model-3.ms2 – Linien der abgeleiteten Rumpfform
In Modell model-3.ms2 werden für die Ausgangsform und die abgeleitete Form auch das verdrängte Volumen und sein Längenschwerpunkt LCB bestimmt. Zur Berechnung dieser hydrostatischen Größen werden Hydrostatic Reals verwendet. Näheres zu diesen Funktionen wird im Tutorium 14 mitgeteilt.
Für den abgeleiteten Rumpf wird als Contour List die Entity List hydro_contours_derived verwendet. Sie enthält die Spantkonturen hydro_stations1_derived, hydro_stations2_derived und hydro_stations3_derived, die den abgeleiteten Rumpf (hull_derived) und das Deck (Ruled Surface deck) schneiden. Analog gibt es für den Basis-Rumpf als Contour List die Entity List hydro_contours_parent mit hydro_stations1_parent, hydro_stations2_parent und hydro_stations3_parent.
Zur Anzeige der Werte dient die Entity List view_hydro_data. Diese im Entities Manager auswählen, dann das Real Values-Anzeigefenster öffnen mit Taste "V" oder Hauptmenü/ Tools/ Real Values.
Volumen und LCB der abgeleiteten Rumpfform lassen sich manuell durch die „Schieberegler“-Beads bead3 und bead4 auf gewünschte Werte einstellen. Der Basis-Rumpf verdrängt auf der CWL 13.30 m^3, LCB liegt bei 7.70 m. Soll beispielsweise das Volumen 10% größer sein (14.64 m^3) bei gleichem LCB, muß der t-Parameterwert von bead3 auf den Wert von 0.1258 und der von bead4 den Wert 0.1435 gesetzt werden. Was sich nur durch schrittweises Herantasten herausfinden läßt.

Modell model-3.ms2 – durch Verschieben der Beads bead3 und bead4 kann manuell die abgeleitete Rumpfform geändert werden, bis Volumen und LCB gewünschte Sollwerte annehmen.
5 Automatische Anpassung der abgeleiteten Mcs für Sollwerte von Volumen und LCB
Wie sich automatisch die abgeleiteten Mcs für Sollwerte von Volumen und LCB finden lassen, ist in Modell model-4.ms2 gezeigt. Im Gegensatz zum vorherigen Modell model-3.ms2 wird nun der t-Parameterwert der beiden Beads bead3 und bead4 durch die beiden Variablen ex_1 and ex_2 definiert. Dadurch ist es möglich, ein Solve Set-Objekt zu verwenden, um curve_x so zu bestimmen, dass Volumen und LCB des abgeleiteten Rumpfes bestimmte Sollwerte annehmen.
Die beiden Variablen Vol_target und LCB_target legen die gewünschten Werte für Verdrängungsvolumens und Längenschwerpunkt LCB fest. Der Solve Set solveset1 justiert automatisch die Variablen ex_1 und ex_2 so, dass die Hydrostatic Reals Vol_derived und LCB_derived gleich groß sind wie Vol_target und LCB_target.
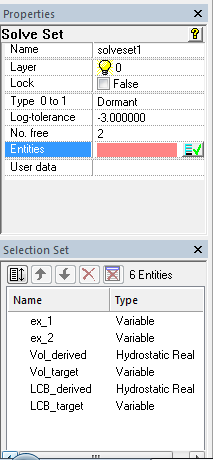
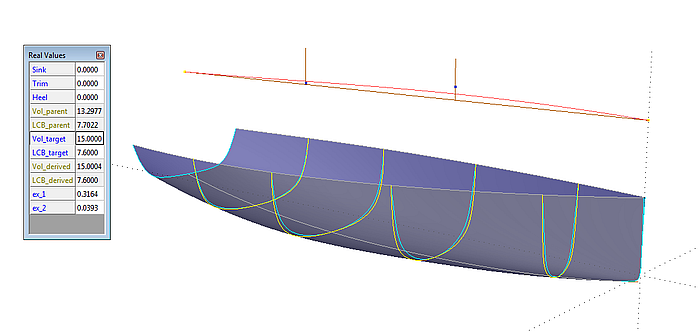
Modell model-4.ms2 – der Solve Set solveset1 mit 2 Freiheitsgraden (Variablen ex_1 und ex_2) paßt die Verschiebungskurve curve_x für die abgeleiteten Mcs automatisch so an, dass das Volumen und sein Längenschwerpunkt den Vorgabewerten entsprechen.

Modell model-4.ms2 – größeres Volumen und LCB nach achtern verschoben
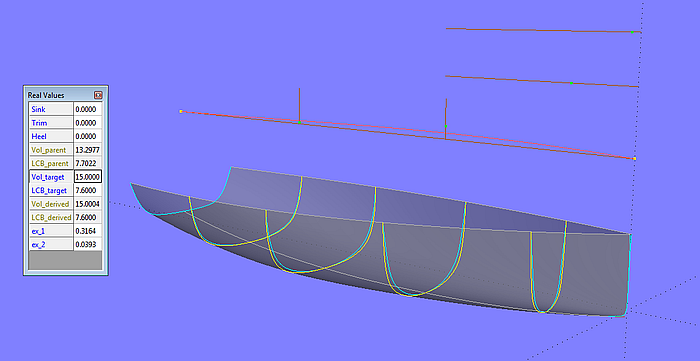
Modell model-4.ms2 – größeres Volumen und LCB nach vorne verschoben
6 Export der abgeleiteten Rumpfform
Sind die Werte für Volumen und LCB wie gewünscht, ist es praktisch, aus dem abgeleiteten Rumpf eine alleinstehende Rumpffläche zu machen. Da die abgeleiteten Cps (D22, D23, D24 etc.) Arc-length Beads sind, also keine freien 3-D Punkte, hängen sie von einer Reihe von Formeln und Variablen ab. Darum ist es nicht möglich, den abgeleiteten Rumpf als Komponente zu speichern, denn alle Eltern-Objekte der abgeleiteten Cps wären in der Komponente mitenthalten.
Zwar läßt es sich nur auf die abgeleiteten Mcs anwenden, aber mit Hilfe von Iges-Export sind nur wenige Schritte auszuführen, um eine unabhängige Fläche zu erhalten. Durch den Iges-Export erhalten die abge-leiteten Mcs unabhängige Kontrollpunkte.
- Auswählen aller Mcs der C-spline Lofted Surface hull_derived
- Hauptmenü/ File/ Export 3D/ IGES. Im Options-Dialogfenster “Selection Set Only“ auswählen. Dann Schaltfläche „OK” und die Iges-Datei unter gewünschtem Namen speichern.
- Import der Iges-Datei über File/ Import/ IGES in das Zielmodell. Abschließend mit den importierten Mcs eine C-spline Lofted Surface im Zielmodell erzeugen.

Modell model-4.ms2 – Export der abgeleiteten Mcs als Iges-Datei um unabhängige Cps zu erzeugen
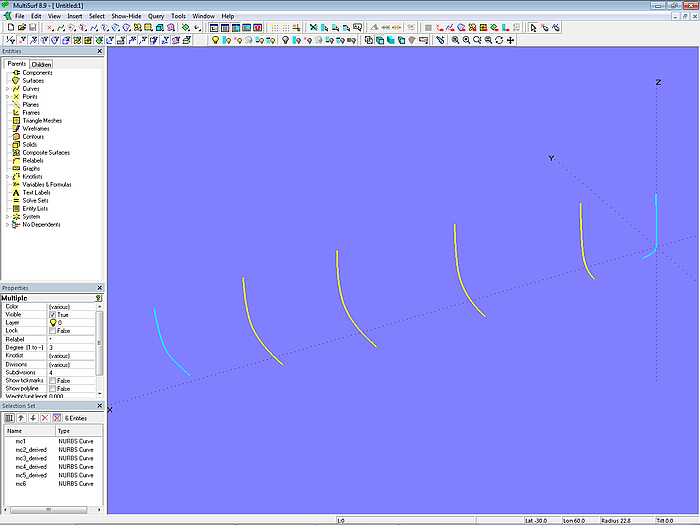
Import der Iges-Datei mit unabhängigen Mcs in das Zielmodell zur Weiterbearbeitung
7 Import eines Basis-Rumpfes
Das an Hand von Modell model-4.ms2 beschriebene Verfahren, aus einem Basis-Rumpf eine neue Rumpfform für Sollwerte von Volumen und LCB abzuleiten, läßt sich auch in Modelle übertragen, die mit einer anderen Anzahl von Mcs und Cps aufgebaut sind. Folgende Modelle liegen zur Zeit vor:
Modell model-4.ms2 – C-spline Lofted Surface, 6 mcs x 6 cps
Modell model-5.ms2 – C-spline Lofted Surface, 5 mcs x 6 cps
Modell model-6.ms2 – C-spline Lofted Surface, 5 mcs x 4 cps
Soll in eines dieser Modelle (empfangendes Modell, z. B. model-4.ms2) ein anderer Basis-Rumpf importiert werden, müssen lediglich dessen Cps übergeben werden. Hierzu gibt es zwei Möglichkeiten.
- Save Component / Load Component: man macht von den Cps des anderen Basis-Rumpfes eine Komponente und lädt diese dann in das empfangende Modell (z. B. model-4.ms2.
- Iges Export / Iges Import: man exportiert die Cps des anderen Basis-Rumpfes als Iges-Datei und importiert sie dann in das empfangende Modell (z. B. model-4.ms2.
Anschließend werden im empfangenden Modell (model-4.ms2, model-5.ms2, model-6.ms2) an jeder Mc die alten Cps durch die entsprechenden neuen Cps über Hauptmenü/ Tools/ Adopt Children ersetzt. Dabei sind im „Adopt Children“-Dialogfenster die Kontrollkästchen „Delete old parent“ und „Transfer name to new parent“ mit einen Haken zu versehen (aktivieren). Die C-spline Lofted Surface hull_parent im Modell erhält so die Cps des neuen Basis-Rumpfes.
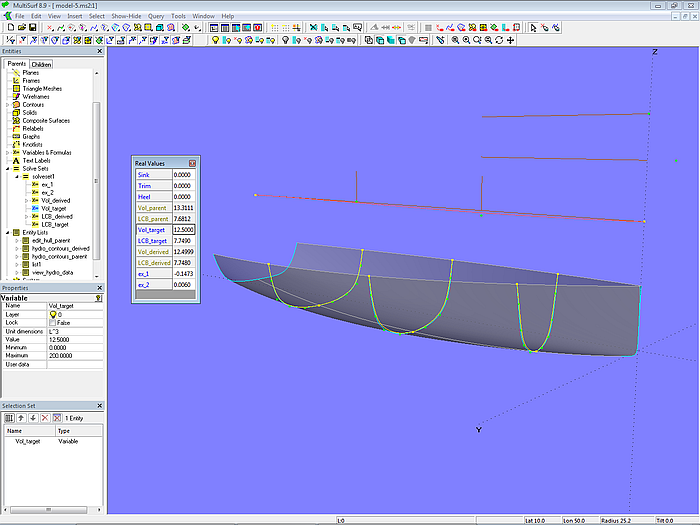
Modell model-5.ms2 – Beispiel für Basis-Rumpf und abgeleiteten Rumpf (C-spline Lofted Surface, 5 Mcs x 4 Cps)
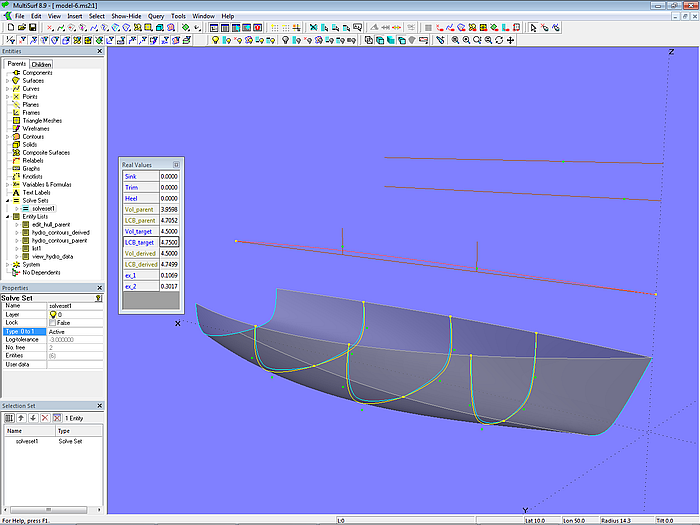
Modell model-6.ms2 – Beispiel für Basis-Rumpf und abgeleiteten Rumpf (C-spline Lofted Surface, 5 Mcs x 4 Cps)
Appendix 1
On Systematic Variation of Hull Forms - the Lackenby Method
H. Lackenby did research work on the variation of ship forms (On the systematic geometrical variation of ship forms; TINA, 1950). In the following the attempt is explained to implement his method in a MultiSurf model.
Start point is a basis hull form and its section area curve based on a set of stations. To change prismatic coefficient and/or LCB, the stations are moved towards bow or stern. That is, the shape of each station is unchanged, just its position is adjusted a bit.
Lackenby devides the hull in forebody and afterbody. Both have a certain length. The necessary shift dx of each station follows the formula: dx = c * x * (1 –x), where x is the location of the station. c is a constant, its value depends on the required change in prismatic coefficient and LCB.
For x = 0 (bow or stern) or x = 1 (midship), dx = 0. That means, the midship station and the end stations of bow and stern remain fixed (dx = 0), only the stations in between are shifted in a specific fashion.
In the MultiSurf model Lackenby-1.ms2 the author tried to implement the method of Lackenby.
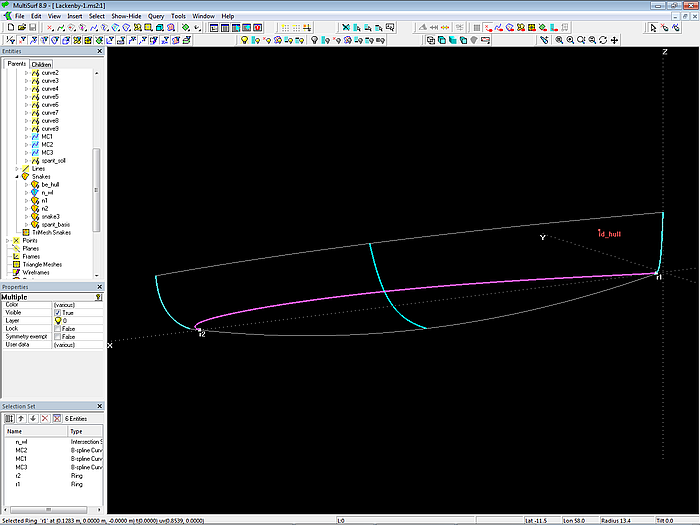
Model Lackenby-1.ms2
The hull is a C-spline Lofted Surface supported by 3 mcs. The forward end of the waterline is the Ring r1, the aft end is Ring r2.
For this hull the section area curve is constructed following these steps:
- Line l1 runs from r1 to r2.
- Bead e1 is on Line l1.
- At the location of e1 the waterline and the fairbody curve are intersected in the XYZRings r3 and r4.
- Line l2 is spanned between r3 and r4 and projected onto the hull surface as Projected Snake n1. Note, that the parent for Mirror/surface is the Bead e1 – so the projection rays originate from this point, thus there will not be a problem with projection failure due to a parallel projection ray and surface tangent.
- n1 is projected onto the centerplane (*Y = 0) as projected Curve curve1.
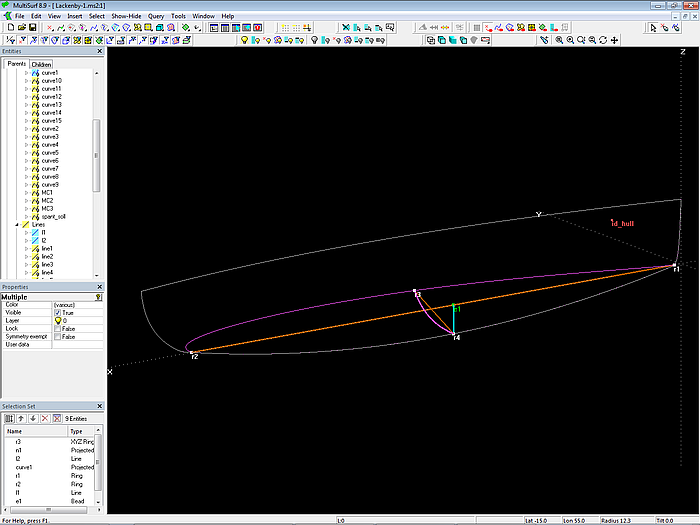
Model Lackenby-1.ms2 – construction of an immersed half-section
Finally the Ruled Surface immersed_half_section is created between n1 and curve1.
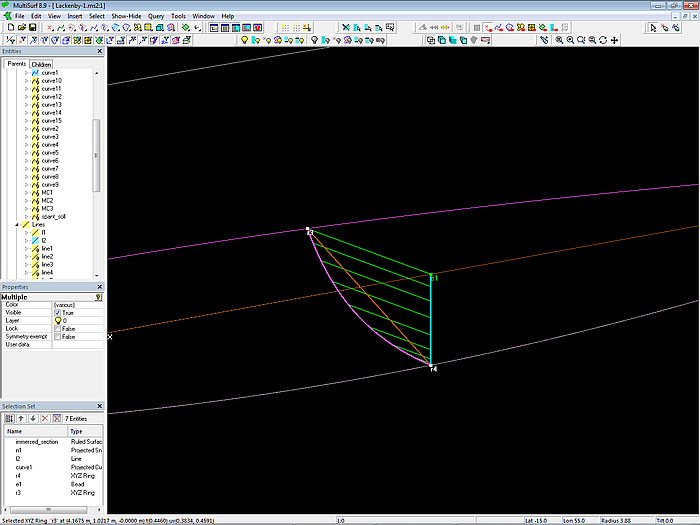
Model Lackenby-1.ms2 – immersed half-section
So now we have the immersed half-section at the position of e1.
By the Formula area_immersed the size of the complete immersed section is calculated. This value is assigned to the Z-coordinate of Point pt1, which represents the abscissa of the section area curve at position of e1.
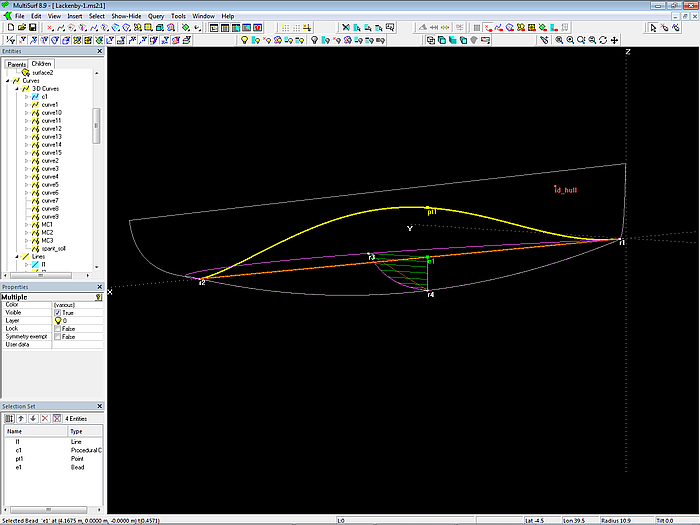
Model Lackenby-1.ms2 – section area curve by repeating the half-section construction by a Procedural Curve entity
When the t-position of e1 is changed from t = 0 to t = 1 we get the complete section area curve. The Procedural Curve c1 does this construction, creating the path of pt1.
Finally the Ruled Surface section_area_total is created between c1 and l1.
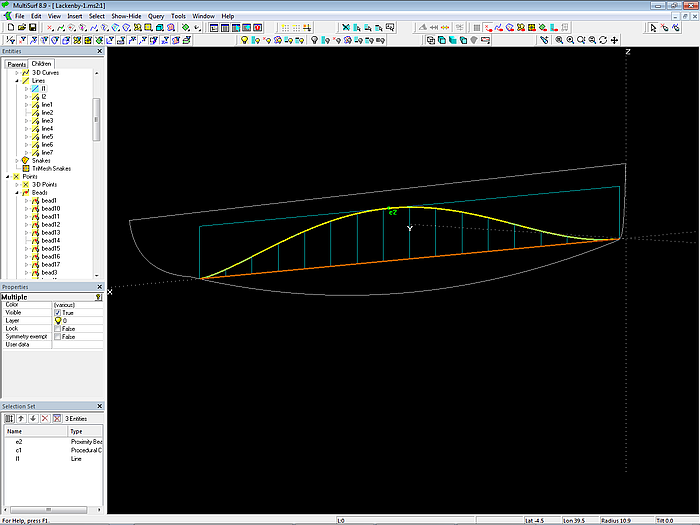
Model Lackenby-1.ms2 – section area curve
The Proximity Bead e2 on the section area curve determines the location of the maximum section area, the midship section. Note, that in general, this is not at Lwl/2.
The total prismatic coefficient is the ratio of the section area and the area of the surrounding rectangle. The Formula cp_total calculates this value.
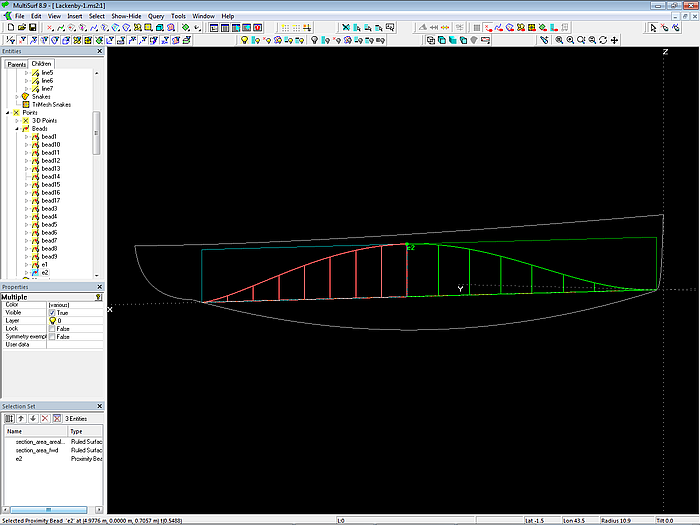
Model Lackenby-1.ms2 – section area curves of forebody and afterbody
Dividing the section area curve at e2 results in the section area curve of the forebody and the section area curve of the afterbody. Again, the prismatic coefficient of the forebody and the prismatic coefficient of the afterbody is calculated as the ratio between the respectives area and the area of the encompassing rectangle.
Change the position of the LCB keeping the total prismatic coefficient constant
Now let us assume, we want to move the LCB towards the bow by, say 0.2 m. The total prismatic coefficient should be kept constant, i.e. the displaced volume is unchanged. According to the Lackenby method we must move the stations towards the bow. How much a station must be moved can be calculated with the following formulas given by Lackenby.
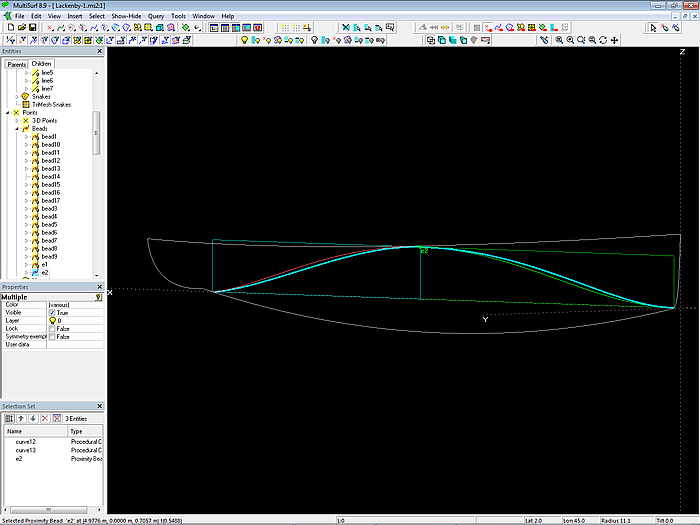
Model Lackenby-1.ms2 – modified section area curve to change the LCB
The necessary longitudinal shift d_xaft of the section at x to produce the required change in prismatic coefficient of the section area curve of the afterbody:
d_xaft = caft * x * (1-x) equal to: d_xaft = caft * (x – x^2)
with
caft = d_cpaft / (cpaft – 2 * 2cpaft * xaft)
The necessary longitudinal shift d_xfwd of the section at x to produce the required change in prismatic coefficient of the section area curve of the forebody:
d_xfwd = cfwd * x * (1-x) equal to: d_xaft = caft * (x – x^2)
with
d_xfwd = d_cpfwd / ( cpfwdt – 2 * 2cpfwd * xfwd )
where:
d_cpaft: the required change in prismatic coefficient of the section area curve of the afterbody
d_cpfwd: the required change in prismatic coefficient of the section area curve of the forebody
cpaft: the prismatic coefficient of the original section area curve of the afterbody
cpfwd: the prismatic coefficient of the original section area curve of the forebody
xaft: the fractional distance from midships of the centroid of the original section area curve of the afterbody
xfwd: the fractional distance from midships of the centroid of the original section area curve of the forebody
d_cpaft = ( 2 * dz * cptotal )/ ( haft + hfwd )
d_cpfwd = - ( 2 * dz * cptotal ) / ( haft + fwd )
where:
dz: the required fractional shift of the LCB in the modified form
cptotal: the total prismatic coefficient of the basis hull
haft: the fractional distance from midships of the centroid of the added sliver of area to the original section area curve of the afterbody
hfwd: the fractional distance from midships of the centroid of the added sliver of area to the original section area curve of the forebody
The first approximation of haft and hfwd is given by:
haft = ( 2 * xaft -3 * kaft^2 ) / ( 1 – 2 * aft )
hfwd = ( 2 * xfwd -3 * kfwd^2 ) / ( 1 – 2 * xfwd )
where:
xaft: the fractional distance from midships of the centroid of the original section area curve of the afterbody
xfwd: the fractional distance from midships of the centroid of the original section area curve of the forebody
kaft: radius of gyration about midships of the original section area curve of the afterbody
kfwd: radius of gyration about midships of the original section area curve of the forebody
All those quantities of the original section area curves of forebody and afterbody are calculated in the model by formulas and variables. Except the moments of inertia of the section areas of forebody and afterbody. The values Izz_aft and Izz_fwd are variables, the values are taken from the Mass Properties. So, if the original section area curve is changed because the basis hull is changed, those values must be looked up in main menu/ Tools/ Mass Properties and edited in the variables Izz_aft and Izz_fwd.
The results are displayed by Text Label entities.
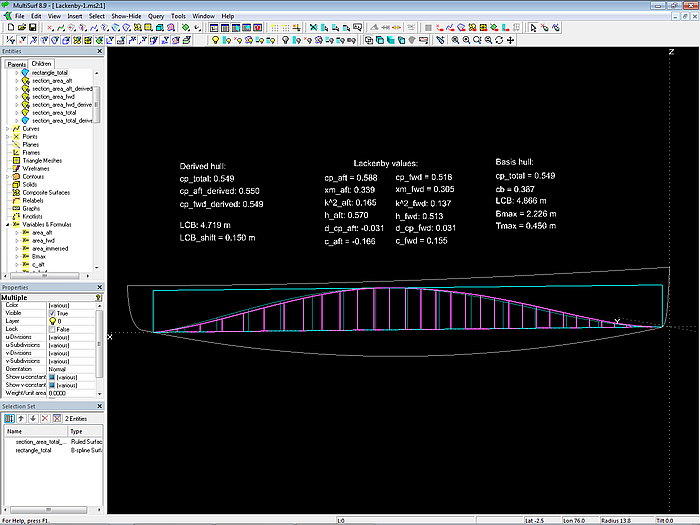
Model Lackenby-1.ms2 – calculation of station respacing
For a given value of the variable LCB_shift the model calculates the new section area curves of foreship and aftship and the required new location of stations. For one station this is shown below - a basis station (cyan) is shifted to the new position (magenta).
This readjustment can now be done with any set of stations required.
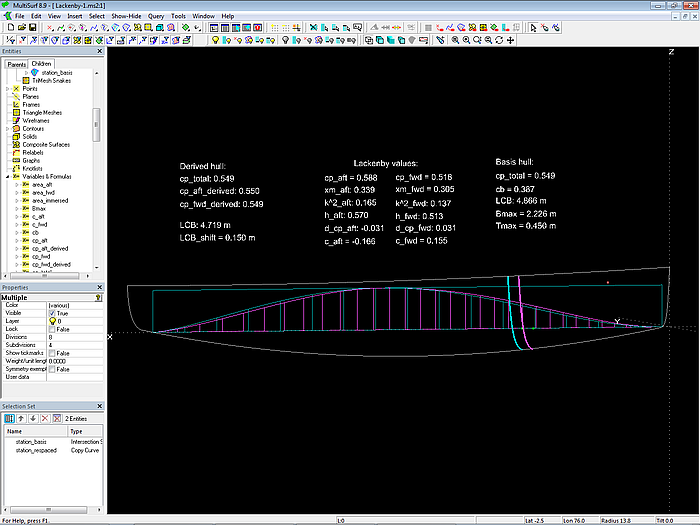
Model Lackenby-1.ms2 – adjustment of station position
To summarize: with the model Lackenby-1.ms2 it is possible to calculate the shift of stations to achieve a required LCB position keeping the volume constant.
But we do not get a surface model, we get just new station positions. At present there is no idea, how the original surface model must be modified in order to be in agreement with the new total section area curve.
I wonder if we do need a method to directly manipulate the master curves of a hull surface, and not its section area curve.
Appendix 2
On Automated Adjustment of Hull Form – MC Relocation
In model LCB_shift-1.ms2 a possible strategy is shown. Display the Real Values window (Tools/ Real Values) in order to show volume, LCB etc.
The two inner mcs of the hull surface are defined on a common basis point, the bead e1. Moving e1 will change the longitudinal position of the mcs and thus the LCB.
The volume will also change, but not much, if the LCB shift is moderate.
In this model both inner mcs will move the same distance, which is equal to the shift of e1. This means, if we have more than two inner mcs, the mcs at the extremes will move the same distance, what could cause full ends.
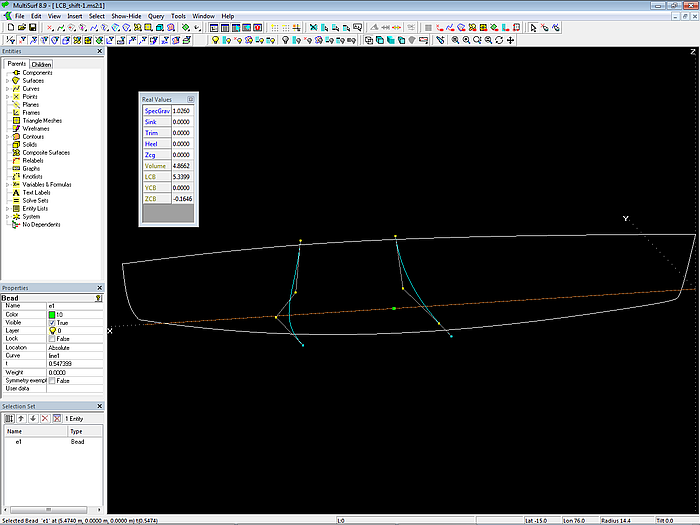
Model LCB_shift-1.ms2 – the two inner mcs can be moved by shift of their common point of reference.
Model LCB_shift-2.ms2 shows an example where the shift of mcs decreases towards the hull ends. Change Variable c and the mcs will shift in a harmonic fashion.
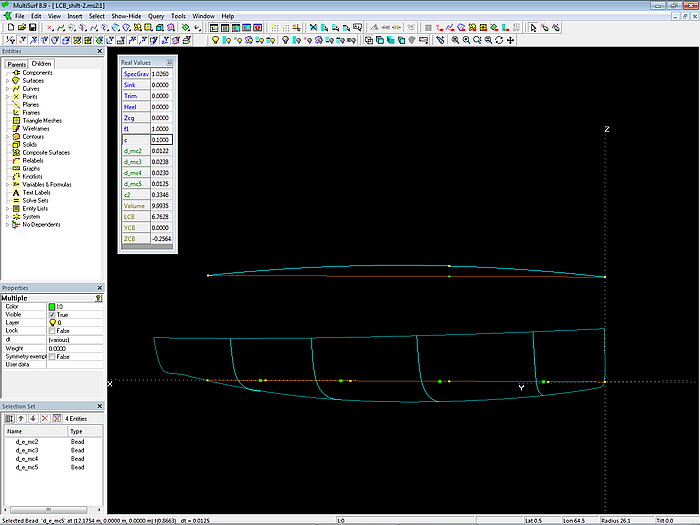
Model LCB_shift-2.ms2: the relocation of mcs decreases towards the hull ends.
There are disadvantages:
The volume is not constant. A simple solution would be to scale the model in Y direction according to the ratio (volume required / volume existing). However, that would change the beam.
The coordinates of the control points of the mastercurves are not simple numbers, but depend on a series of formulas and variables. However, via Iges-Export and an Iges re-import into the target model the dependencies can be dissolved.
======================================================================================