B-spline-Kurven und B-spline-Flächen
Eigenschaften und Anwendungen
von Reinhard Siegel
Inhalt
Einleitung
1 B-spline Curve
- 1.1 Grundlagen
- Wie sieht eine B-spline Curve aus?
- Polygonzug – Ähnlichkeit
- Grad
- Tangentialeigenschaft
- Cp-Verschiebung – lokaler Effekt
- Krümmungsverlauf
- 1.2. Anwendungen
- B-spline Curve als Stützkurve für Flächen
- Tangentiale Verbindung von Bug-Mc und Bodenkontur
- Radius Arc und B-spline Curve
2 B-spline Surface
- 2.1 Grundlagen
- Degree
- Lokale Kontrolle
- Tangentialeigenschaft
- 2.2 Anwendungen
- Rumpf - Rundspant
- Rumpffläche inklusive Bugrundung
- Ebene Fläche
- Tangentialebene
3 B-spline Lofted Surface
- 3.1 Grundlagen
- C-spline Lofted Surface vs B-spline Lofted Surface
- 3.2 Anwendungen
- Beispiele aus den Tutorien 8, 10 und 13
- Spezielle Bodengeometrie
- Rumpf mit Propellertunnel
Einleitung
B-spline-Kurven sind mit wenigen Kontrollpunkten leicht zu formen, sie schwingen nicht, sie beginnen und enden immer auf die gleiche Weise. Diese geometrischen Eigenschaften machen sie zu sehr praktischen Freiformkurven, zum Beispiel als Masterkurven für Rumpf, Deck oder Aufbauten. B-spline-Flächen als ihre Erweiterung haben ebenfalls diese geometrischen Eigenschaften. Im Folgenden soll gezeigt werden, wie sich mit B-spline-Kurven und -Flächen viele Geometrieaufgaben lösen lassen.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point); synonym verwendet
Mc: Masterkurve, Stützkurve (master curve, support curve); synonym verwendet
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
1 B-spline-Kurven
1.1 Grundlagen
Wie sieht eine B-spline Curve aus?
Die Eltern einer B-spline Curve sind eine Reihe von Kontrollpunkten (Cps). Dies können freie Punkte im Raum sein (Point), oder Punkte auf Kurven oder Flächen (Bead, Ring). Die gerade Verbindung der Cps heißt Polygonzug der B-spline Curve. Ein Beispiel zeigt Modell b-spline_curve-1.ms2.

Modell b-spline_curve-1.ms2 – Zusammenhang zwischen Cp-Anordnung und Kurvenverlauf
Polygonzug – Ähnlichkeit
Der Kurvenverlauf hängt eng mit der Form des Polygonzugs zusammen. Die Kurve beginnt im ersten Cp und endet im letzten Cp, verläuft er nicht durch die inneren Cps. Sie ist eine „Annäherung“ (Approximation) an den Polygonzug. Im Gegensatz zur C-spline Curve, die immer durch alle Kontrollpunkte verläuft (Interpolation). Man kann sich die Cps auch als Federn denken, die die Kurve anziehen.

Kurvenvergleich – eine B-spline Curve ist „weich“, sie folgt eng der Polylinie durch ihre Kontollpunkte. Eine C-spline Curve verhält sich wie eine Straklatte.
Eine B-spline Curve ist „weich“, sie schwingt nicht, eine C-spline Curve verhält sich wie eine Straklatte. Eine deutlich gekrümmte Kurve läßt sich mit einer B-spline Curve mit weniger Kontrollpunkten modellieren als mit einer C-spline Curve.
Eine B-spline Curve wird nicht durch eine einzige, von Anfang bis Ende gültige mathematische Funktion bestimmt, sondern durch mehrere abschnittsweise gültige Formeln. Durch entsprechende Randbedingungen wird sichergestellt, dass beim Übergang von einem Abschnitt zum nächsten keine Lücke entsteht, kein Knick auftritt (stetige Steigung) oder kein Krümmungssprung auftritt (stetige Kurvenkrümmung).
Grad (Degree)
Abgesehen von der Anordnung der Cps spielt noch der Grad (Degree) der B-spline Curve eine Rolle. Dies ist aus Modell b-spline_curve-2.ms2 ersichtlich.
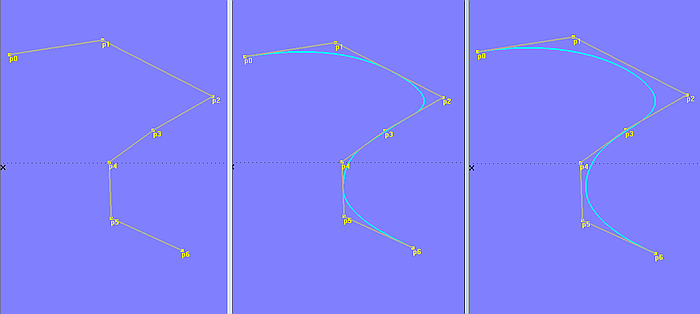
Modell b-spline_curve-2.ms2 – der Parameterwert „Degree“ bestimmt, wie eng die Kurve dem Polygonzug folgt (links: Degree = 1; Mitte: Degree = 2; rechts: Degree = 3)
Ist Degree = 1, verläuft die Kurve wie der Polygonzug, von Punkt zu Punkt gerade. Wird Degree auf den Wert 2 gesetzt, berührt die Kurve jeweils den Mittelpunkt der inneren Segmente des Polygonzugs. Bei Degree = 3 ist der Kurvenverlauf noch etwas weiter vom Polygonzug entfernt. Je größer der Grad einer B-spline Curve, umso freier folgt sie der Anordnung der Cps. Sie behält aber immer Ähnlichkeit zum Polygonzug.
Der maximal mögliche Wert für Degree einer B-spline Curve ist gleich n-1, wobei n die Anzahl der Cps ist.
Tangentialeigenschaft
Aus den vorstehenden Abbildungen geht auch hervor, dass eine B-spline Curve stets tangential zum ersten Polygonsegment beginnt, und stets tangential zum letzten Polygonsegment endet. Diese Tangentialeigenschaft ist von überaus praktischem Nutzen.
Liegen zum Beispiel wie im Modell b-spline_curve-3.ms2 cp1 und cp2 vertikal übereinander (Y-Koordinaten gleich), dann beginnt die Kurve vertikal (kein Spantausfall oder –einfall), ganz gleich, wie cp3 angeordnet ist. Soll die Mc normal zur Mittschiffsebene enden, müssen nur der vorletzte und der letzte Cp in der Z-Koordinate übereinstimmen.
Über die Tangentialeigenschaft lassen sich auf einfache Weise solche geometrischen Bedingungen fest im Modell verdrahten.
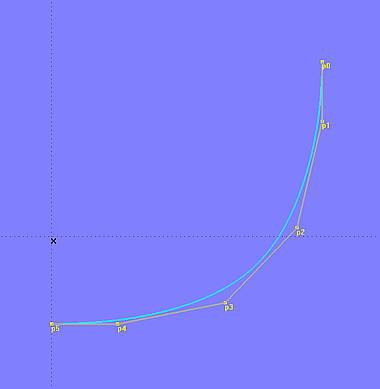
Modell b-spline_curve-3.ms2 – die Tangentialeigenschaft der B-spline Curve ist nützlich, wenn zum Beispiel eine Masterkurve vertikal beginnen und horizontal enden soll.
Cp-Verschiebung – lokaler Effekt
B-spline Curves weisen eine weitere Besonderheit auf. Verschiebt man einen Cp einer B-spline Curve, dann ändert sich nicht der gesamte Verlauf, sondern lediglich ein Teil. Dies ist Folge der abschnittsweise definierten Kurvenfunktion. Verschiebt man beispielsweise den Anfangspunkt einer B-spline Curve mit Degree = 2, dann ändert sich ihre Form nur bis zum Mittelpunkt des Polygonsegments zwischen dem 2. und 3. Cp, alles andere bleibt gleich. Siehe Modell b-spline_curve-3a.ms2.
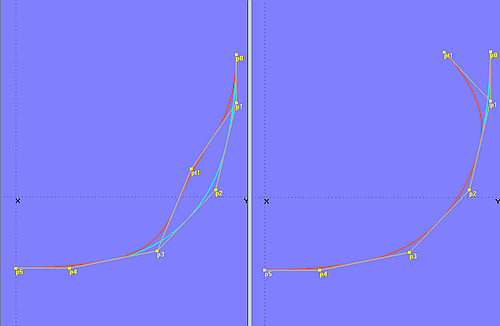
Modelle b-spline_curve-3a.ms2 und b-spline_curve-3b.ms2 – lokaler Einfluß der Kontrollpunkte
Verschiebt man einen inneren Kontrollpunkt, ändert sich der Kurvenverlauf nur in seiner Nachbarschaft (Modell b-spline_curve-3b.ms2). Ein Kontrollpunkt hat nur einen bestimmten lokalen Einfluß auf den Kurvenverlauf. Je höher der Wert für Degree, umso mehr wirken sich Änderungen auf die gesamte Form aus.
Krümmungsverlauf
Eine Kurve strakt, wenn sich ihre Krümmung im Verlauf harmonisch ändert. Über Hauptmenü/ View/ Display/ Profile/ Curvature oder die entsprechende Toolbar-Schaltfläche läßt sich der Krümmungsverlauf anzeigen.
Am Beispiel von Modell b-spline_curvature.ms2 soll gezeigt werden, welchen Einfluß die Anordnung der Kontrollpunkte auf den Krümmungsverlauf hat. Kurve c0 (Degree = 3) hat im Bereich der maximalen Krümmung einen Einschnitt. Die Krümmung nimmt erst ab, dann wieder zu, der Verlauf ist unharmonisch. Dagegen weist Kurve c1 (Degree = 3) einen harmonischen Krümmungsverlauf auf. Beide Kurven liegen übereinander, haben die gleiche Form, nur die Position der inneren Cps ist unterschiedlich.
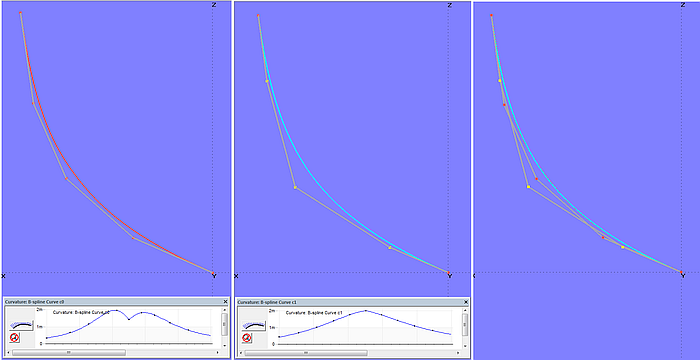
Modell b-spline_curvature.ms2 – beide B-spline Curves liegen übereinander, unterscheiden sich aber im Krümmungsverlauf.
Dass man bei gleicher Anzahl der Cps ein und die gleiche Kurvenform erzielen kann, aber mit jeweils etwas anderer Anordnung der inneren Cps, ist eine weitere Besonderheit bei B-spline Curves. Einem harmonischen Verlauf der Krümmung entlang der Kurve ist der Vorzug zu geben. Oftmals reicht es bereits, den zweiten sowie vorletzten Cp etwas näher an den Anfang beziehungsweise an das Ende der Kurve zu verschieben, um einen lokalen Abfall der Krümmung zu beheben.
1.2 Anwendungen
B-spline Curve als Stützkurve für Flächen
Eine B-spline Curve ist mit wenigen Kontrollpunkten (Cps) leicht zu formen, ohne dass sie zwischen den Cps schwingt. Bis auf den ersten und den letzten Cp verläuft sie zwar nicht durch ihre Kontrollpunkte, die Kurvenform ähnelt aber stets dem Polygonzug durch ihre Kontrollpunkte. Außerdem beginnt die B-spline Curve immer tangential zur Linie zwischen dem 1. und 2. Cp und endet immer tangential zur Linie zwischen dem vorletzten und letzten Cp. Diese Tangentialeigenschaft ist sehr nützlich, möchte man eine bestimmte Richtung an den Kurvenenden festlegen.
Rumpfflächen
Der Rumpf eines Bootes oder einer Yacht ist in Querrichtung (Spantrichtung) sehr viel stärker gekrümmt als in Längsrichtung. Mit B-spline Curves lassen sich Masterkurven für alle möglichen Hauptspantformen formen, von Rundspant bis Langkiel. Bei gleicher Kurvenform erfordert eine C-spline Curve mehr Kontrollpunkte, folglich mehr Aufwand beim Straken.
Deck, Aufbau, Anhänge
Wenig Kontrollpunkte, kein Schwingen und die Tangentialeigenschaft – mit diesen Vorteilen der B-spline Curve lassen sich Flächen für Decks, Aufbauten, Kiele etc. modellieren. Dabei können sie als stützende Kurven verwendet werden oder als erzeugende Kurven (B-spline Lofted Surface).
Beispiele werden in Abschnitt 3.2 vorgestellt.
Tangentiale Verbindung von Bug-Mc und Bodenkontur
Modell tangent_bow_mc.ms2 zeigt, wie sich eine B-spline Curve, die als Bug-Mc verwendet werden soll, festverdrahtet tangential an die Bodenkontur anschließen läßt.
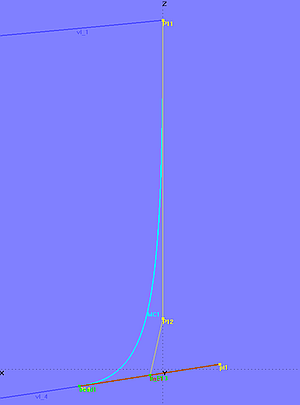
Modell tangent_bow_mc.ms2 – MC1 läuft tangential in die Bodenkontur ein, da e_P13 auf der Tangente im Anfangspunkt von vl_4 liegt.
Radius Arc und B-spline Curve
Ein Radius Arc in Kombination mit einer B-spline Curve ergibt einen zweckmäßigen Kurvenzug. Zum Beispiel als Pfad für eine Sweep Surface, als Mittellinie einer Rohrleitung oder für den Ausschnitt eines Fensters. Modell RadiusArc_B-spline.ms2 zeigt das Prinzip, wie sich beide Kurven glatt aneinander anschließen lassen.
Der Radius Arc von Typ = 3 beginnt tangential zur Linie zwischen seinen Kontrollpunkten 1 und 2 und endet tangential zur Linie zwischen Kontrollpunkt 2 und 3. Um also eine B-spline Curve tangential mit einem Radius Arc von Typ = 3 an dessen t = 0-Ende zu verbinden, setzt man einen Bead mit t = 0 auf den Radius Arc und verwendet diesen Bead als 1. Cp und den Kontrollpunkt 2 als 2. Cp für die B-spline Curve. Diese Konstruktion stellt den glatten Anschluß dauerhaft sicher.
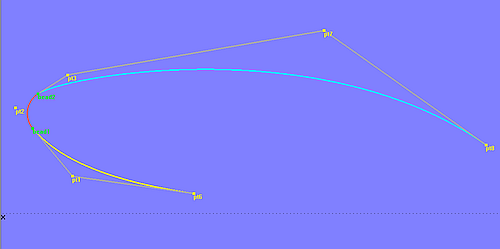
Modell RadiusArc_B-spline.ms2 – glatte Verbindung zwischen B-spline Curve und Radius Arc
2 B-spline Surface
2.1 Grundlagen
Die Kontrollpunkte einer B-spline Surface bilden ein vierseitiges Polygonnetz. Dieses Netz formt die Fläche ähnlich wie bei einer B-spline Curve der Polygonzug der Kontrollpunkte. Bis auf die vier Eckpunkte des Netzes liegen die Kontrollpunkte außerhalb der Fläche. Man kann sich die Form einer B-spline Surface so vorstellen, als sei sie über Federn mit den inneren Kontrollpunkten verbunden. Der Verlauf der Ränder einer B-spline Surface entspricht dem von B-spline Curves, definiert mit den entsprechenden Randpunkten. Modell bsurf-1.ms2 zeigt ein Beispiel
Degree
Wie eine B-spline Curve hat auch eine B-spline Surface die Eigenschaft „Degree“, und zwar je einen Degree-Wert für ihre Längsrichtung (u) und einen Degree-Wert für ihre Querrichtung (v).
Je kleiner der Wert für Degree, umso näher verläuft die Fläche am Netz. Je höher Degree, umso geringer die Anziehung, umso „straffer“ die Fläche.
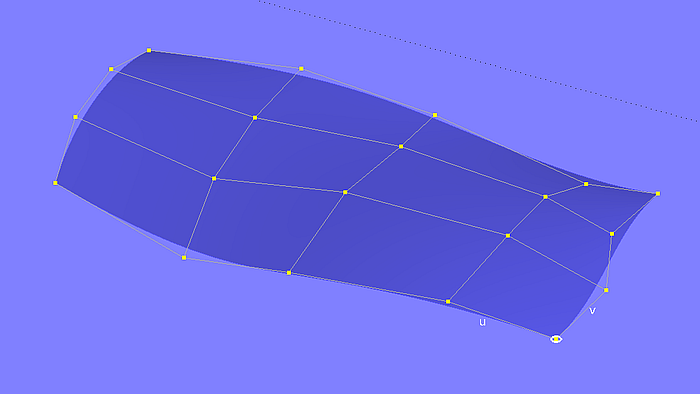
Modell bsurf-1.ms2 – B-spline Surface mit Polygonnetz der Kontrollpunkte (5 Cps in u-Richtung, 4 Cps in v-Richtung)
Die B-spline Surface folgt ihrem Polygonnetz, sie schwingt nicht darüber hinaus. Bis auf die Eckpunkte liegen ihre Cps alle außerhalb der Fläche.
Lokale Kontrolle
Ähnlich wie bei einer B-spline Curve ist der Effekt eines Kontrollpunktes auf die Form der B-spline Surface lokal (Modell bsurf-2.ms2). Je größer der Wert für Degree, umso globaler wird der Einfluß.

Modell bsurf-2.ms2 – rote und gelbe Schnitte zeigen den lokalen Einfluß der Verschiebung eines Kontrollpunkts.
Tangentialeigenschaft
Analog zur B-spline Curve verfügt die B-spline Surface ebenfalls über eine Tangentialeigenschaft. Diese Eigenschaft läßt sich praktisch nutzen, wie in den folgenden Anwendungsfällen gezeigt wird.

Modell bsurf-3.ms2 – die Cps in v-Richtung der 1. und 2. Reihe sind senkrecht zueinander. Die B-spline Surface beginnt normal zur Mittschiffsebene entlang der Kante u = 0.
2.2 Anwendungen
Rumpf – Rundspant
Modell bsurf_hull.ms2 zeigt einen mit 5 x 4-Kontrollpunkten definierten Rundspantrumpf.
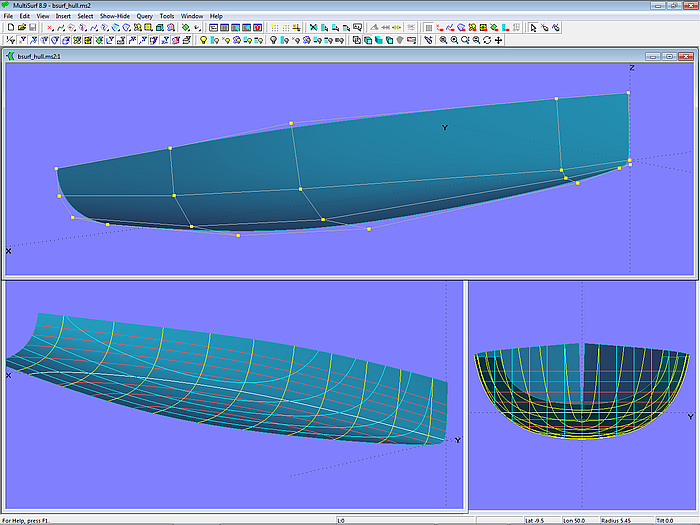
Modell bsurf_hull.ms2 – Rundspantrumpf als B-spline Surface (5 x 4 Cps)
Das Modell nutzt die Tangentialeigenschaft der B-spline Surface, damit entlang der Bodenkontur die Fläche normal zur Mittschiffsebene endet. Dazu haben alle Cps dieser Kante (P24, P34, P44 usw.) auf Mitte Schiff die gleiche Z-Koordinate wie ihre entsprechenden Nachbarpunkte (P23, P33, P43 etc.).
Rumpffläche inklusive Bugrundung
Modell bsurf_hull_w_bowround.ms2 ist ein weiteres Beispiel dafür, wie ein bestimmtes Formmerkmal über die Tangentialeigenschaft fest in eine B-spline Surface eingebaut werden kann. Hier ist die Bugrundung nicht eine separate Fläche, sondern Teil der Rumpffläche. In Längsrichtung (u-Richtung) werden 6 Cps verwendet. Damit der senkrechte Einlauf zur Mittschiffsebene gewährleistet ist, sind die Cps entlang der Stevenkontur Projected Points der Cps der in v-Richtung nächstgelegenen Reihe.
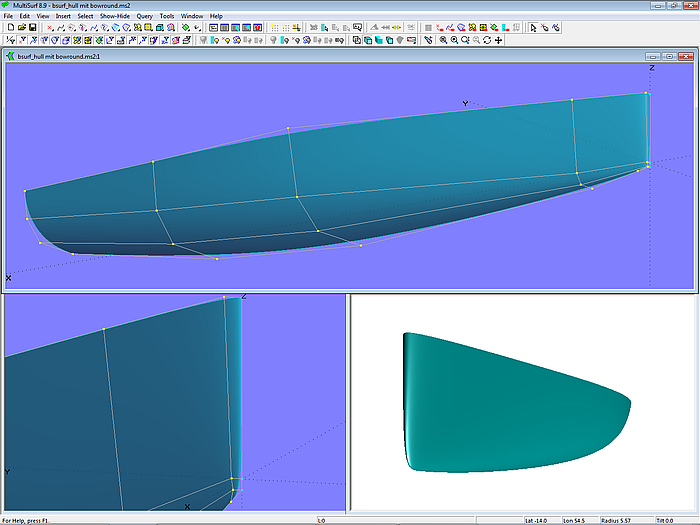
Modell bsurf_hull_w_bowround.ms2 – Bugrundung als Teil der Rumpffläche
Ebene Fläche
Gelegentlich wird in einem Modell eine einfache ebene Fläche benötigt, zum Beispiel als Basisfläche für einen Bauspant oder ein anderes planes Bauteil. Mit einer ebenen Fläche läßt sich auch eine 2-point Plane oder 3-point Plane ersetzen, die den Nachteil hat, immer so groß wie das gesamte Modell angezeigt zu werden. Das ist der Übersichtlichkeit abträglich – was nur lokal gebraucht wird, muß sich nicht über das ganze Modell erstrecken.
Eine ebene Fläche läßt sich auf verschiedene Weise erzeugen. Zum Beispiel als Translation Surface, mit je einer Line für Erzeugende und Leitkurve. Oder als Ruled Surface zwischen zwei parallelen Linien. Mit geringstem Aufwand an Objekten läßt sie sich als B-spline Surface mit 2 x 2 Cps generieren. In Modell planar_bsurf.ms2 ist dies gezeigt. Mit den 3 Punkten p1, p2 und p3 läßt sich die Lage der Fläche im Raum bestimmen, während der Copy Point p4 dafür sorgt, dass alle 4 Punkte in einer Ebene liegen. Mit diesen 4 Punkten ist die B-spline Surface planar_surface definiert. Der Degree-Wert der Fläche ist in u- und v-Richtung gleich 1.
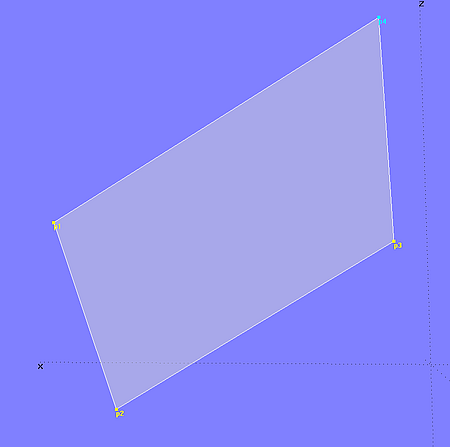
Modell planar_bsurf.ms2 – ebene Fläche mit dem Minimum an Objekten als B-spline Surface( Degree = 1 in u- und v-Richtung)
Ebene B-spline Surface als Basisfläche für einen Bauspant
Tangentialebene
Aus Modell tangent_bsurf.ms2 ist zu ersehen, wie die Tangentialebene in einem Flächenpunkt konstruiert werden kann. Mit Magnet m0, Offset Point pt01 und Point pt02 relativ zu m0 wird der 3-point Frame F0 bestimmt. In der YZ-Ebene des Frames liegt Punkt p1, ein Eckpunkt der Tangentialebene. Punkt p1 wird nun zum einen an der Y-Achse des Frames gespiegelt als Mirror Point p2 (2. Eckpunkt), zum anderen am Magnet m0 als Mirror Point p3 (3. Eckpunkt). Der 4. Eckpunkt ist der Copy Point p4. Mit diesen Eckpunkten wird abschließend die B-spline Surface tangent_surface erzeugt.

Modell tangent_bsurf.ms2 – Tangentialebene im Flächenpunkt m0 (Magnet) als B-spline Surface
Verschiebt man m0, ändert sich die ganze Konstruktion entsprechend. Mit p1 läßt sich Breite und Länge der ebenen Fläche den Erfordernissen anpassen.
Natürlich kann eine Tangentialebene im Punkt m0 auch als 2-point Plane mit m0 und dem Offset Point pt01 erzeugt werden. Aber auf die hier vorgestellte Weise läßt sich die Größe der planen Fläche kontrollieren. Außerdem liefert ihre Position im Modell Information, zu welchem Zweck sie dient. Das Modell wird übersichtlicher.
3 B-spline Lofted Surface
3.1 Grundlagen
Bei einer C-spline Lofted Surface werden die Mcs mit C-spline Curves “beplankt”. Werden statt dessen B-spline Curves verwendet, erhält man eine B-spline Lofted Surface.
Wie bei einer B-spline Curve, die im ersten Cp beginnt und im letzten Cp endet, beginnt die B-spline Lofted Surface an der ersten Mc und endet an der letzten Mc. Sie interpoliert aber nicht die inneren Mcs, da eine B-spline Curve ja auch nicht durch die inneren Cps verläuft.
Eine B-spline Lofted Surface folgt ihren Mcs, sie schwingt nicht darüber hinaus.
Für die Mcs einer B-spline Lofted Surface können Kurven unterschiedlicher Art verwendet werden. Zum Beispiel ist im Modell bloftsurf.ms2 die vorletzte Mc eine C-spline Curve, die letzte Mc ein Kreisbogen (Arc).
Mit einer B-spline Lofted Surface läßt sich vorteilhaft die Tangentialeigenschaft von B-splines nutzen, um sie ohne Knick an eine andere Fläche anzuschließen oder sie entlang ihrer Kanten auf eine bestimmte Art und Weise enden zu lassen.

Modell bloftsurf.ms2 – B-spline Lofted Surface: Masterkurven unterschiedlichen Typs werden mit B-spline Curves „beplankt“.
Sind bei einer B-spline Lofted Surface alle Mcs vom Typ B-spline Curve mit gleicher Anzahl Cps und gleichem Degree-Wert, dann ist die Fläche identisch mit einer B-spline Surface mit den gleichen Kontrollpunkten. Durch ihre andere Organisation ist die B-spline Lofted Surface aber überschaubarer. Man kann am Verlauf ihrer Mcs die Flächenform in ihrer Umgebung leicht ersehen.

Modelle bulb_b-spline_surface.ms2 und bulb_b-spline_lofted_surface.ms2 – Ballastbulb als B-spline Surface (oben) und als B-spline Lofted Surface (unten)
C-spline Lofted Surface vs B-spline Lofted Surface
Da sie steif ist, benötigt eine C-spline Curve mehr Stützpunkte, um sie in eine stark gekrümmte Form zu bringen. Also erfordert eine stark gekrümmte Fläche mehr Mcs, wenn sie durch eine C-spline Lofted Surface erzeugt werden soll. B-spline Curves sind weich, mit wenigen Cps zu formen und verfügen über die Tangentialeigenschaft, was die B-spline Lofted Surface attraktiv für Flächen mit örtlich großer Krümmung macht.
3.2 Anwendungen
Tutorien 8, 10 und 13 – B-spline Lofted Surfaces
In den Tutorien 8, 10 und 13 werden Anwendungsfälle für B-spline Lofted Surfaces mitgeteilt. Tutorium 8 (On the rounding of bows, sterns, sharp waterlines and on the attachment of keels) zeigt, wie Bug- und Heckrundungen erzeugt werden können oder sich eine separate Kielfläche tangential an den Rumpf anschließen läßt. Tutorium 10 (Ballastkiele) und Tutorium 13 (Decks und Aufbauten) beschreiben Strategien und Methoden, mit B-spline Lofted Surfaces Kiele, Ballastanhänge oder Aufbauten zu modellieren.
Hier einige Beispiele. Eine detailierte Beschreibung ist in den genannten Tutorien zu finden.
Anschluß Kiel – Rumpf
In Modell attached_keel.ms2 ist für eine klassische Segelyacht der Kiel einschließlich des tangentialen Übergangs zum Rumpf definiert als B-spline Lofted Surface mit 6 Mcs. (Tutorium 8)
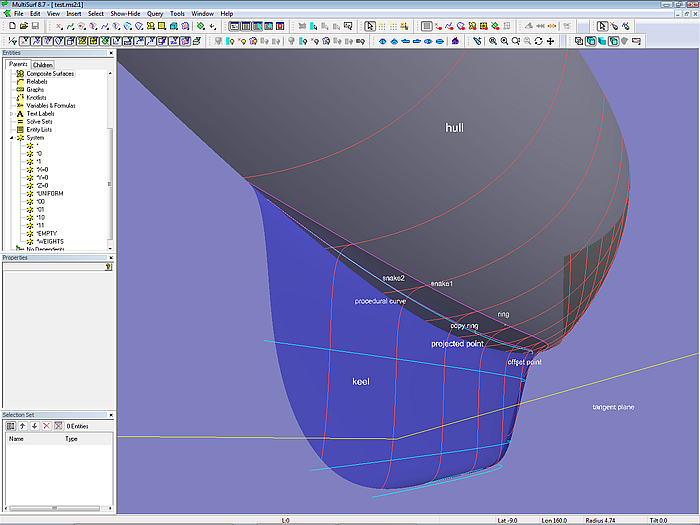
Modell attached_keel.ms2 - Kielfläche (B-spline Lofted Surface) einer klassischen Segelyacht mit tangentialem Anschluß an den Rumpf. (Tutorium 8)
Bugrundung
Modell tangent_bowround.ms2. (Tutorium 8)
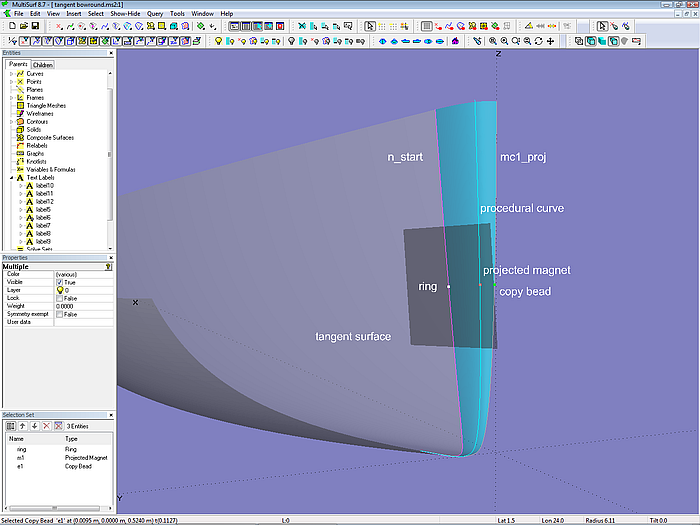
Modell tangent_bowround.ms2 – Bugrundung als B-spline Lofted Surface. (Tutorium 8)
Ballastbulb
Die B-spline Lofted Surface bietet volle Freiheit bei der Gestaltung von Bulbformen für Kielflossen (Modell bulb_b-spline_lofted_surface.ms2. (Tutorium 10)
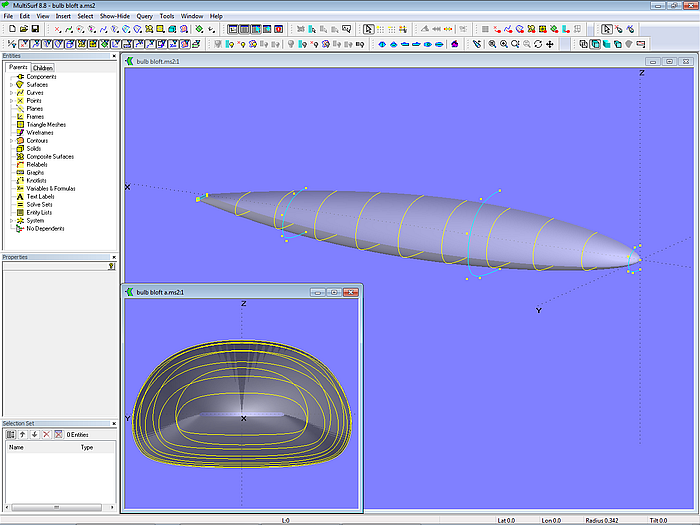
Modell bulb_b-spline_lofted_surface.ms2 – Ballastbulb als B-spline Lofted Surface; Anordnung der Masterkurven. (Tutorium 10)
Aufbau
Modell bubble_cabin_bloft-1.ms2 – runde, weiche Übergänge zwischen Aufbaufront, -seite und –dach durch eine B-spline Lofted Surface mit querlaufenden Mcs. (Tutorium 13)
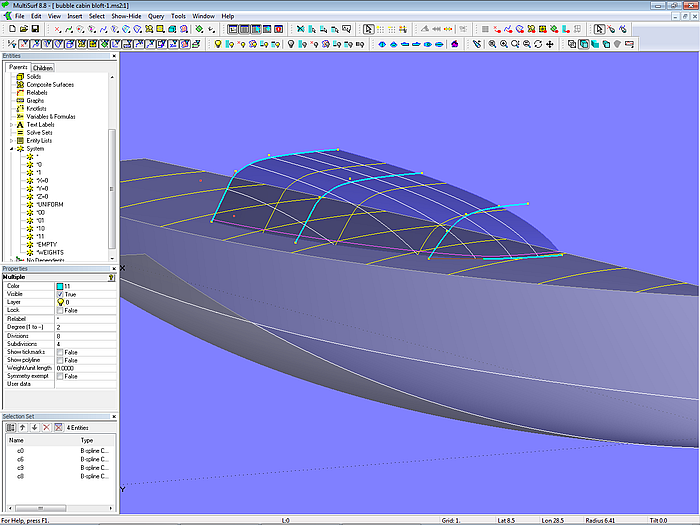
Modell bubble_cabin bloft-1.ms2 – Anordnung der Masterkurven. (Tutorium 13)
Zwei weitere Beispiele für die Verwendung der B-spline Lofted Surface sollen im Folgenden gezeigt werden.
Spezielle Bodengeometrie
Modell bottom.ms2 enthält die Bodenfläche eines Motorbootrumpfes. Entwurfsforderung ist, dass ab einer bestimmten Längsposition die Schnitte exakt gerade verlaufen.
Dazu ist die Bodenfläche in ein Bugteil und ein Heckteil unterteilt. Die Basisfläche des Heckteils ist die Translation Surface bottom_aft_0, aufgespannt mit der in Längsrichtung laufenden Line l0 und der B-spline Curve mc_bottom_aft_0, die in Spantrichtung verläuft. Den vorderen Teil der Bodenfläche bildet die B-spline Lofted Surface bottom_fwd, gestützt von 5 Mcs. Während die vorderen 3 Mcs freie B-spline Curves sind, liegen die beiden letzten Mcs als B-spline Snakes auf der Heckfläche. Dadurch läuft die Bugfläche tangential in die Heckfläche ein.
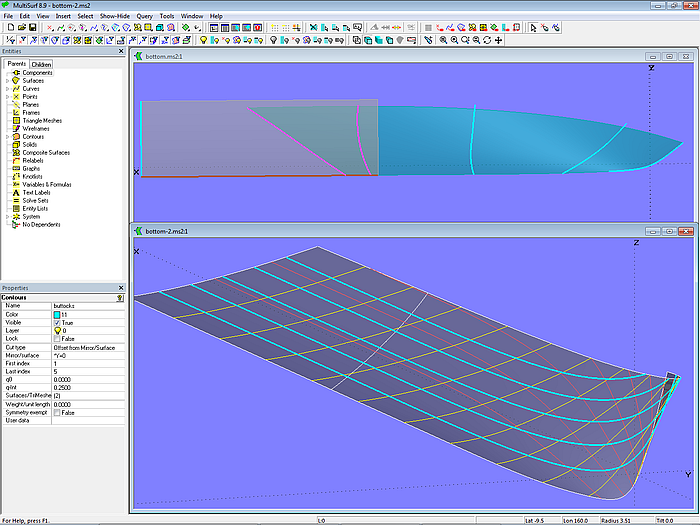
Modell bottom.ms2 – Bodenfläche mit geradem Verlauf der Schnitte im Hinterschiff
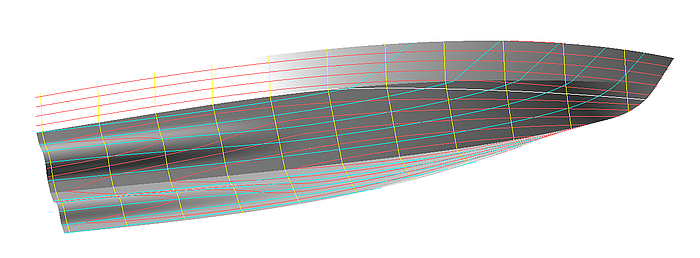
Rumpf mit Propellertunnel
Modell tunnel_stern.ms2 zeigt, wie ein Propellertunnel in die Bodenfläche eines Motorbootrumpfes eingefügt werden kann. Basisfläche des Bodens ist die C-spline Lofted Surface bottom_0. Tunnelfläche ist die B-spline Lofted Surface tunnel, bestimmt durch 6 in Längsrichtung verlaufenden Mcs.
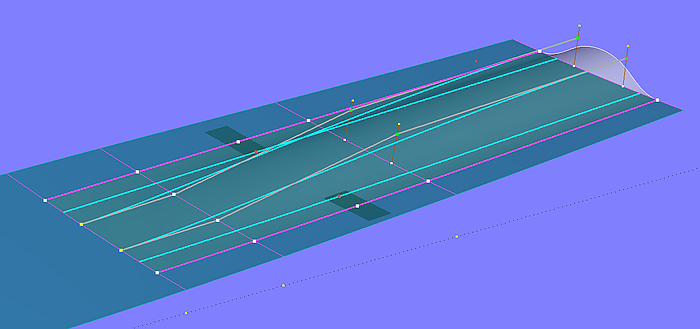
Modell tunnel_stern.ms2 – Propellertunnel als B-spline Lofted Surface mit 6 Mcs
Die Rand-Mcs sind B-spline Snakes auf der Bodenfläche. Die beiden mittleren Mcs sind B-spline Curves, sie formen Größe und Verlauf der Tunnelhöhe in Quer- und Längsrichtung. Den tangentialen Einlauf des Tunnels in den Boden stellen die beiden Procedural Curves mc2_tunnel und mc5_tunnel sicher; ihre Konstruktion sorgt dafür, dass bei diesen beiden Mcs jeder Kurvenpunkt auf der Tangentialebene im korrespondierenden Kurvenpunkt auf der jeweils benachbarten Rand-Mc liegt.
Die fertigen Teilflächen des Bodens werden durch SubSurfaces erzeugt.
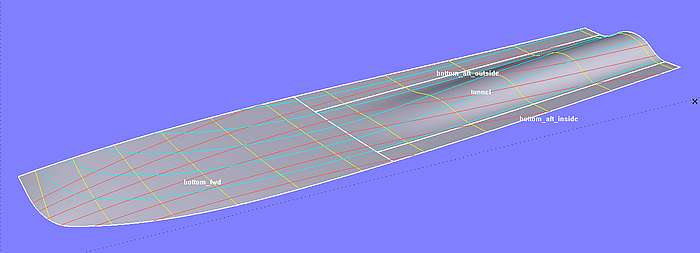
Modell tunnel_stern.ms2 – die fertigen Teilflächen des Bodens werden durch SubSurfaces erzeugt.
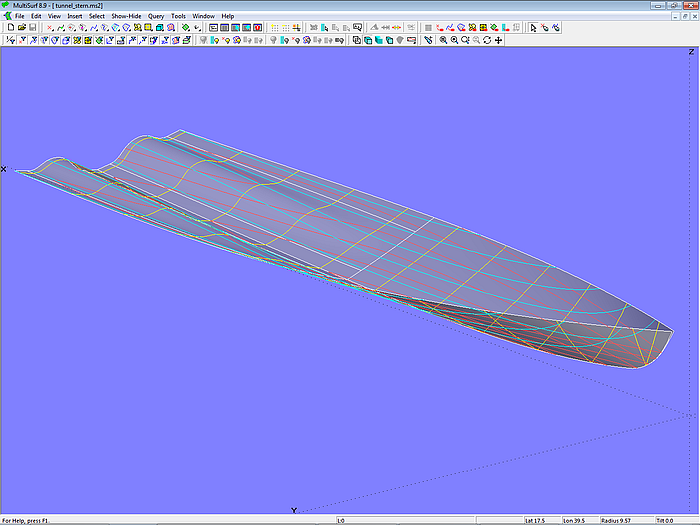
Modell tunnel_stern.ms2 – Motorbootboden mit Propellertunnel
======================================================================================