Das Solve Set-Objekt
Über iterative Lösungen von Geometrieproblemen
von Reinhard Siegel
Oktober 2020
Inhalt
Einleitung
Das Solve Set-Objekt
Aufgabe 1 – maximale Kurvenbreite
Aufgabe 2 – maximale Rumpfbreite
Aufgabe 3 – Kreisbogen berührt Kurve
Aufgabe 4 – Ellipsenbogen berührt Kurve
Bugrundung mit Ellipsenbögen
Weitere Solve Set-Anwendungen
• Proximity Bead - Kreisbogen berührt zwei Kurven
• Kreisbogen berührt Kurve - Version mit Proximity Bead
• Hydrostatik – freie Schwimmlage
• Automatische Variation der Rumpfform
Einleitung
Es gibt Geometrieprobleme, die nicht einfach zu lösen sind. Man konstruiere beispielsweise eine Linie, die durch einen bestimmten Punkt verläuft und einen Kreis tangiert. Oder man bestimme die maximale Breite einer Kurve oder eines Rumpfes. Man kann versuchen, diese geometrischen Konstruktionen annähernd und manuell auszuführen, muß sie aber wiederholen, wenn die Basisgeometrie sich ändert. Für derartige Geometrieaufgaben bietet MultiSurf eine dauerhafte, feste Lösung – das Objekt Solve Set.
Dieses Tutorium wurde angeregt durch einen MultiSurf-User, der anfragte, wie sich Wasserlinien eines Bootsrumpfes am Bug elliptisch abrunden lassen. Die Lösung dieses Geometrieproblems macht es erforderlich, den Berührpunkt zwischen Wasserlinien und Ellipsenbögen zu bestimmen. Damit dies ein dauerhafter Teil des Modells ist, muß dazu ein besonderes Objekt verwendet werden – ein Solve Set.
Als Einführung in das Thema Solve Set werden zunächst zwei einfache Beispiele betrachtet. Anschließend wird untersucht, wie sich Mittelpunkt und Radius eines Kreises bestimmen lassen, der eine Kurve berührt. Darauf aufbauend wird der Berührpunkt zwischen einer Ellipse und einer Kurve bestimmt, um dann die Frage nach der elliptischen Bugrundung zu beantworten. Abschließend wird an zwei Beispielen gezeigt, wie sich Solve Set-Objekte bei der Bestimmung der freien Schwimmlage eines Rumpfes und bei der Variation der Rumpfform für Sollwerte von Verdrängung und LCB verwenden lassen.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point); synonym verwendet
Mc: Masterkurve, Stützkurve (master curve, support curve); synonym verwendet
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
Das Solve Set-Objekt
Das Objekt Solve Set ermöglicht Konstruktionen, die allein mit den in MultiSurf zur Verfügung stehenden Punkt-, Kurven- und Flächenarten nicht möglich sind.
Solve Set - characteristische Daten:
Name -- as with any entity
Layer -- as with any entity
Lock -- as with any entity
Type –- 0 (Dormant) or 1 (Active)
Log Tolerance
No. Free –- Number of solve operations
Entities –- Entities required for solve
User data –- as with any entity
Das Solve Set-Objekt erfordert die Eingabe der für die Lösung erforderlichen Objekte in einer bestimmten Struktur:
(1) Freie Objekte mit einer festen Anzahl von Float-Daten: Point, Magnet, Bead, Ring, XPlane, YPlane, ZPlane. Jedes trägt je nach Anzahl der Float-Daten 1 bis 3 Freiheitsgrade für eine Gesamtzahl N Freiheitsgrade (Unbekannte) bei.
(2) Bedingungen. Dies sind N Objektpaare im Muster (Point, Plane/Surface). Jedes dieser Zielpaare stellt eine Gleichheitsbedingung dar. In der gewünschten endgültigen Konfiguration hat jeder Punkt einen Abstand von Null zu seiner entsprechenden Ebene oder Fläche.
Mindestens ein Objekt in jedem Zielpaar muss abhängig von mindestens einem der freien Objekte sein. Solve Set versucht, jeden freien Parameter so anzupassen, dass alle Ziele (Nullabstand) gleichzeitig erreicht werden. Dies erfordert in der Regel eine Iteration. Wenn diese Iteration innerhalb der Toleranz konvergiert, ist die Lösungsoperation erfolgreich und alle beteiligten Objekte bleiben an aktualisierten Positionen.
Das Solve Set-Objekt macht die Lösung zu einem dauerhaften Teil des Modells, wenn Type auf „Active“ gesetzt ist.
Aufgabe 1 – maximale Kurvenbreite
Ein einfaches Problem – wo liegt die breiteste Stelle einer Kurve?
Manuelle Lösung
Betrachten wir hierzu das Modell curve_bmax_manual.ms2. Wo liegt die breiteste Stelle der Kurve c0? Die manuelle Lösung wäre dies: man setzt den Bead e0 auf die Kurve c0 und verschiebt ihn. Dabei beobachtet man den Y-Wert in der Koordinatenzeige in der Status-Zeile.
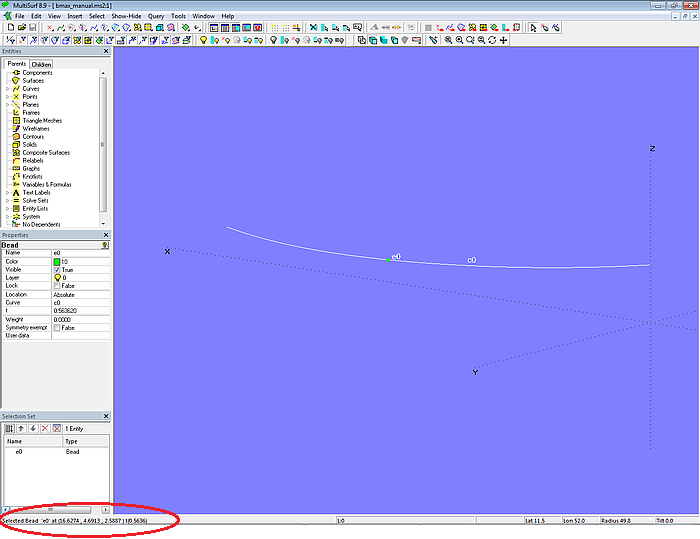
Modell curve_bmax_manual.ms2 – Bestimmung der maximalen Breite mit Bead e0 und Status-Zeile
Ändert sich die Form der Kurve c0, muß die Position von e0 neu bestimmt werden.
Lösung mit Solve Set
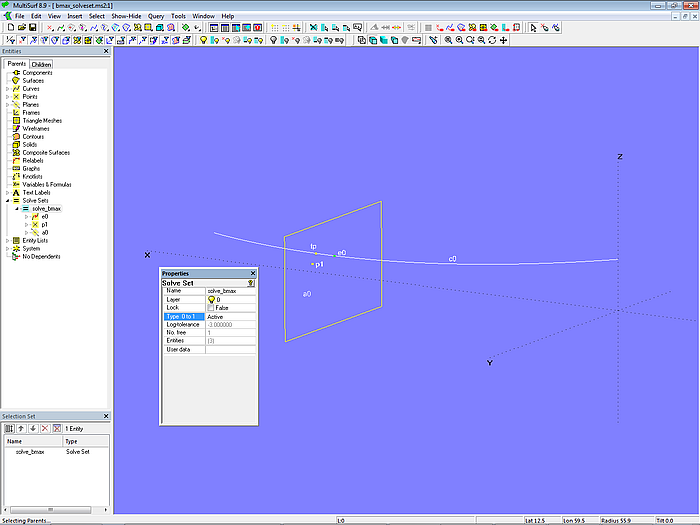
In Modell curve_bmax_solveset.ms2 wird dagegen die Position von e0 mit der maximalen Breite automatisch bestimmt. Dafür wird das Objekt Solve Set verwendet.
Betrachten wir das Modell genauer. Es gibt die Kurve c0. Auf c0 liegt der Bead e0. Er ist Support für den Tangent Point tp. Mit e0 und tp ist die 2-point Plane a0 definiert. Sie ist also die Normalebene der Kurve c0 im Kurvenpunkt e0. Weiterhin gibt es den Point p1, der zu e0 lediglich in Y-Richtung versetzt ist.
Die Objektliste des Solve Sets solve_bmax_curve lautet: {e0; p1; a0}. Das bedeutet: das Solve Set-Objekt soll das freie Objekt e0 so verschieben, dass der Abstand zwischen p1 und a0 zu Null wird (Objektpaar der Lösungsbedingung).
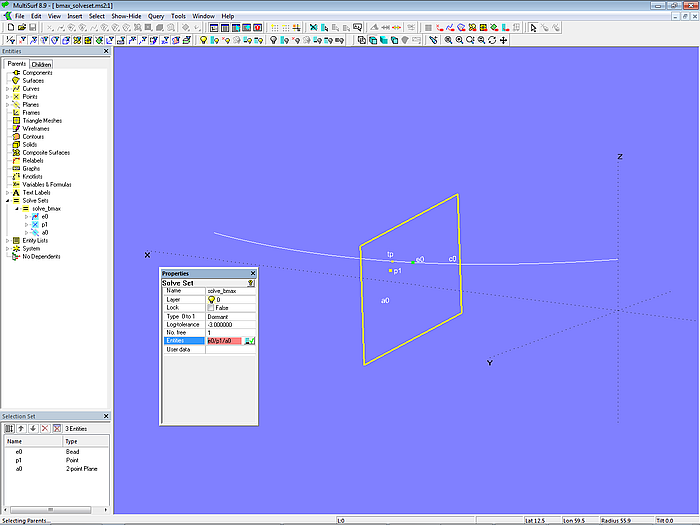
Modell curve_bmax_solveset.ms2 – Solve Set solve_bmax_curve inaktiv (Type = Dormant)
Befindet sich e0 vor der maximalen Breite, liegt p1 hinter der Ebene a0:
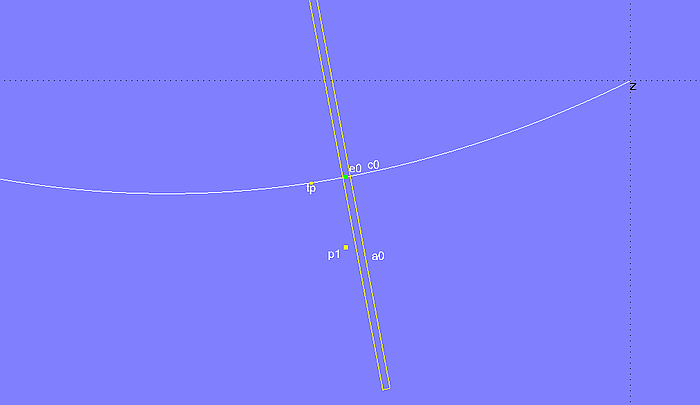
Befindet sich e0 hinter der maximalen Breite, liegt p1 vor der Ebene a0:
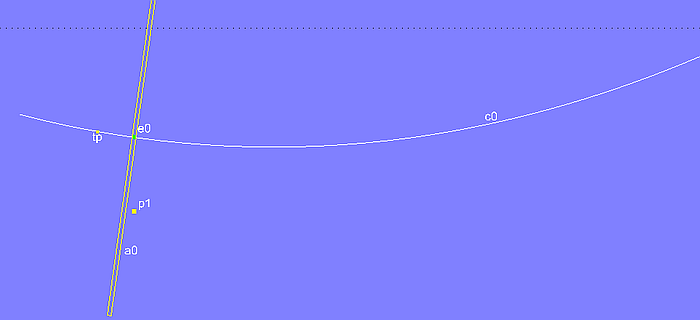
Hat p1 von a0 den Abstand Null, dann befindet sich e0 in der maximalen Y-Position. Genau diesen Punkt bestimmt im Modell curve_bmax_solveset.ms2 das Solve Set-Objekt solve_bmax_curve mit der Liste für freies Objekt und Objektpaar für die Lösungsbedingung: {e0; p1; a0}.
Modell curve_bmax_solveset.ms2 – Solve Set solve_bmax_curve aktiv; für Bead e0 wird automatisch die Position gefunden, für die sich die größte Breite ergibt.
Wird die Kurvenform geändert, wandert e0 automatisch zur größten Breite.
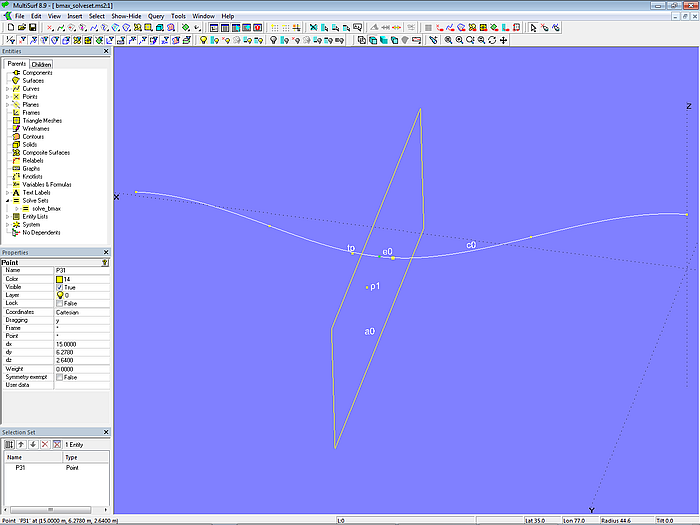
Modell curve_bmax_solveset.ms2 – ist das Solve Set-Objekt aktiv, ist seine Lösung ein dauerhafter Teil des Modells.
Aufgabe 2 – maximale Rumpfbreite
Etwas komplizierter ist die Suche nach der breitesten Stelle eines Bootsrumpfes. Hier gibt es zwei Suchrichtungen – in Längsrichtung und in vertikaler Richtung.
Manuelle Lösung
Mit Modell hull_bmax_manual.ms2 kann nur per Hand die Lösung durch Verschieben des Magnets m0 gefunden werden. Es ist nicht notwendiger Weise so, dass die größte Rumpfbreite an Seite Deck auftritt. Die Spanten könnten einfallend verlaufen.
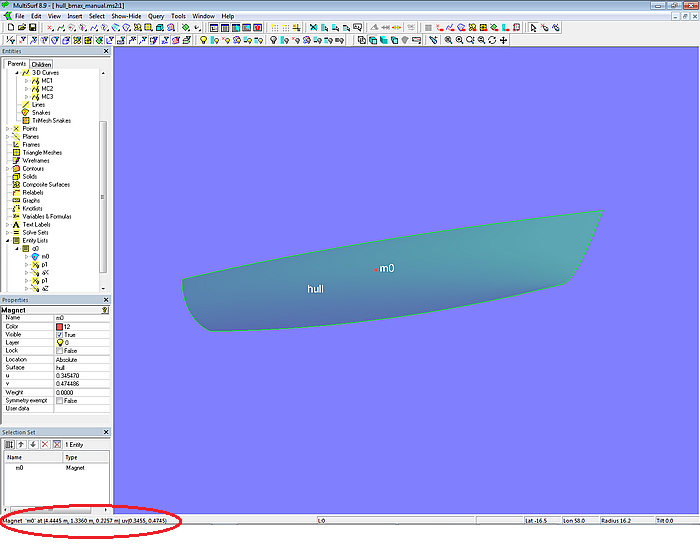
Modell hull_bmax_manual.ms2 – manuelle Bestimmung der maximalen Breite mit Magnet m0 und Status-Zeile
Lösung mit Solve Set
In Modell hull_bmax_solveset.ms2 löst die Aufgabe dagegen das Solve Set-Objekt solve_bmax_hull.
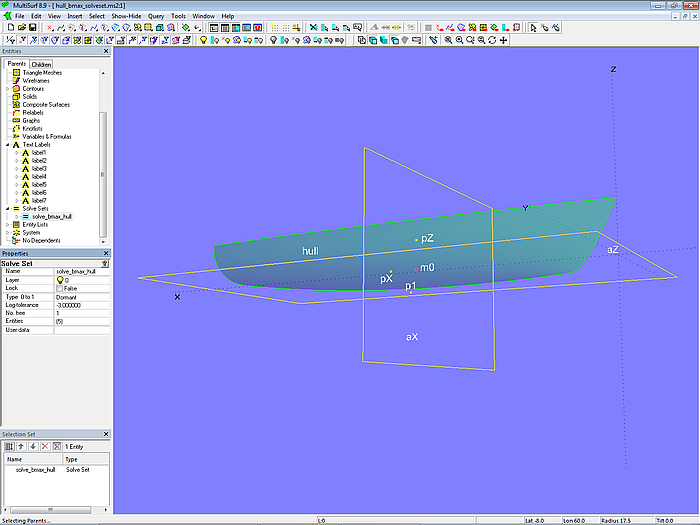
Modell hull_bmax_solveset.ms2 – Solve Set solve_bmax_hull inaktiv
Auf dem Rumpf hull liegt Magnet m0. Relativ zu m0 liegt der in X-Richtung versetzte Point pX sowie der in Z-Richtung versetzte Point pZ. Abhängig von m0 ist auch der Offset Point p1 (er steht senkrecht auf der Rumpffläche). Magnet m0 und Point pX bestimmen die 2-point Plane aX (Spantebene), m0 und pZ die 2-point Plane aZ (Wasserlinienebene).
Das Solve Set-Objekt solve_bmax_hull arbeitet mit der Objektliste {m0, p1, aX; p1; aZ}. Das heißt, die u- und v-Parameterwerte des freien Objekts m0 werden durch Iteration so bestimmt, dass p1 sowohl von aX (Objektpaar für Bedingung 1) als auch von aZ (Objektpaar für Bedingung 2) den Abstand Null hat, also in beiden Ebenen liegt. Dann liegt m0 an der breitesten Stelle des Rumpfes.
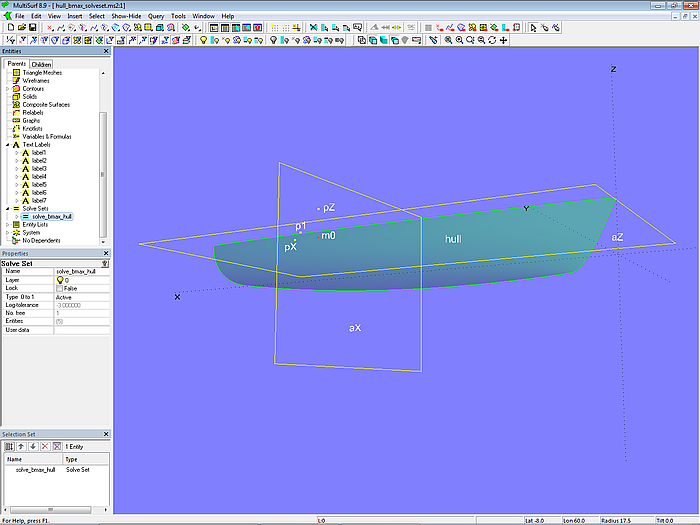
Modell hull_bmax_solveset.ms2 – Solve Set solve_bmx_hull aktiv
Hinweis: Mit den Punktarten Proximity Bead, Proximity Ring und Proximity Magnet lassen sich Aufgabe 1 und Aufgabe 2 ebenfalls lösen.
Aufgabe 3 – Kreisbogen berührt Kurve
Eine Wasserlinie, die am Bug mit einer gewissen Breite endet, soll mit einem Kreisbogen abgerundet werden. Es ist bekannt, wo der Kreisbogen beginnt. Gesucht ist die Position des Mittelpunkts (und damit der Radius), so dass der Kreisbogen die Wasserlinienkurve berührt. Diese Aufgabe ist in Modell arc_tangent_to_curve.ms2 in allgemeiner Weise dargestellt.
Manuelle Lösung
Zum einen gibt es die Kurve c0, zum anderen den Kreisbogen c1 (Arc, Type = 2). Er beginnt im Point p0, sein Mittelpunkt ist der Bead e1 auf der Line l0, und er endet auf der gedachten Linie e1-p2.
Wird e1 verschoben, ändert sich die Lage des Kreismittelpunkts, gleichzeitig auch der Kreisradius, da p0 fest liegt. Manuell läßt sich so eine Position von e1 finden, bei der der Kreisbogen die Kurve berührt.
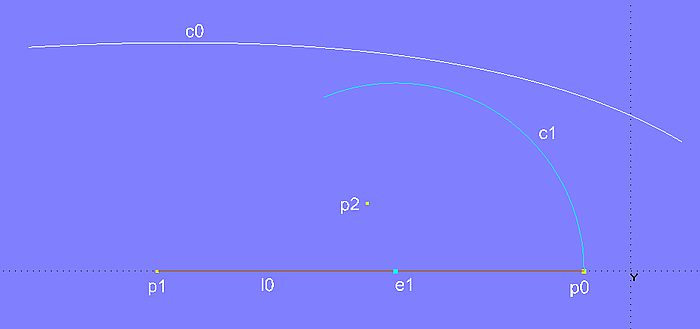
Modell arc_tangent_to_curve.ms2 – gesucht ist die Position des Beads e1, so dass der Kreisbogen c1 die Kurve c0 berührt. Hier ist der Radius (Distanz p0-e1) noch zu klein.
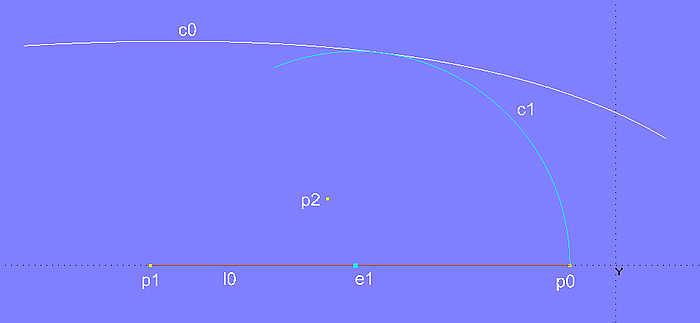
Modell arc_tangent_to_curve.ms2 – manuell ermittelte Position von e1,so dass der Kreisbogen die Kurve berührt.
Ändert sich die Form der Kurve c0, muß die Position von e1 korrigiert werden. Ein Herantasten an die Lösung ist akzeptabel, wen man es im Modell lediglich ein- oder zweimal machen muß. Soll aber die Berührung der Kurve durch den Kreisbogen eine dauerhafte Eigenschaft des Modells sein, muß ein Solve Set-Objekt verwendet werden.
Lösung mit Solve Set
Was sind die geometrischen Bedingungen dafür, dass Kurve c0 vom Kreisbogen c1 berührt wird? Zum einen muß der Abstand zwischen einem Punkt auf dem Kreis und einem Punkt auf der Kurve gleich Null sein. Zum anderen muß die Tangente im Kreispunkt gleich der Tangente im Kurvenpunkt sein. Beziehungsweise es müssen die Normalen gleich sein.
Bei einem Kreis verläuft die Normale immer durch den Mittelpunkt; die Tangente ist senkrecht dazu.
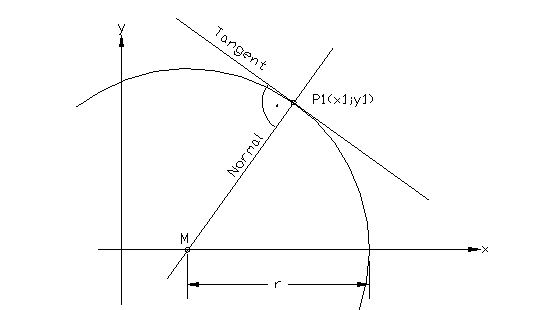
Kreis – die Normale verläuft durch den Mittelpunkt.
Um diese Bedingungen in das Modell arc_tangent_to_curve.ms2 einzubauen, gibt es auf Arc c1 den Bead e2. Davon abhängig ist Tangent Point tp_e2. Mit beiden Punkten ist die 2-point Plane radial definiert. Diese Ebene schneidet die Kurve c0 im Intersection Bead e3. Von e3 abhängig ist der Tangent Point tp_e3. Mit e3 und tp_e3 ist die 2-point Plane normal_to_curve erzeugt. Sie ist die Normale der Kurve c0 im Punkt e3. Diese Ebene schneidet die Line l0 im Intersection Bead C. Mit den Beads e3 und C ist die 2-point Plane tangential definiert. Sie ist die Tangente der Kurve c0 im Punkt e3.
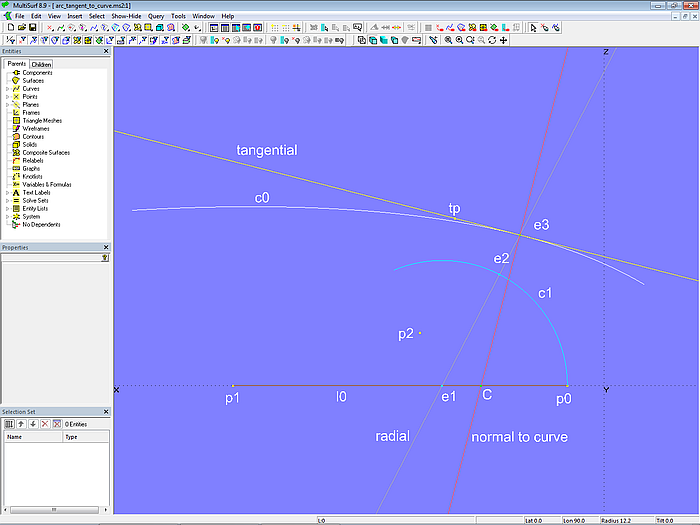
Modell arc_tangent_to_curve.ms2 – Solve Set solve_touch_curve nicht aktiv
Die freien Objekte des Solve Set-Objekts solve_touch_curve sind die Beads e1 und e2. Ihre Position (ihr t-Parameterwert) muß so variiert werden, dass zum einen e1 von der Ebene normal_to_curve den Abstand Null hat (Objektpaar für Bedingung 1). Dann verläuft die Ebene normal_to_curve durch den Kreismittelpunkt, ist also auch Normale an den Kreis. Zum anderen muß gleichzeitig e2 von der Ebene tangential auch den Abstand Null haben (Objektpaar für Bedingung 2). Dann hat e2 auch von e3 den Abstand Null.
Folglich lautet die Liste der für die Lösung erforderlichen Objekte des Solve Set solve_touch_curve: {e1; e2; e1; normal_to_curve; e2; tangential}.
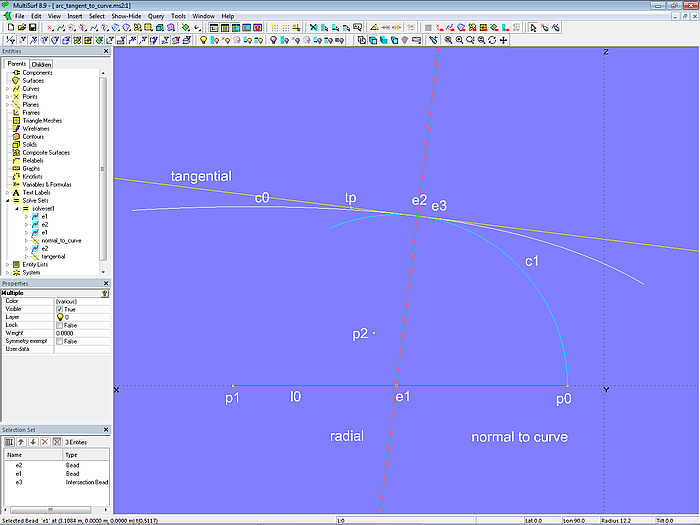
Modell arc_tangent_to_curve.ms2 – Solve Set solve_touch_curve aktiv
Wird die Kurve c0 geändert, findet das Solve Set-Objekt solve_touch_curve automatisch den passenden Kreismittelpunkt (Bead e1).
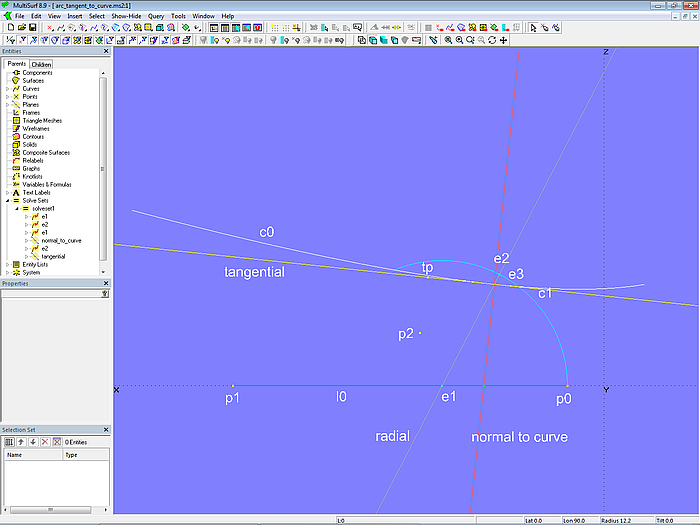
Modell arc_tangent_to_curve.ms2 – Solve Set solve_touch_curve inaktiv
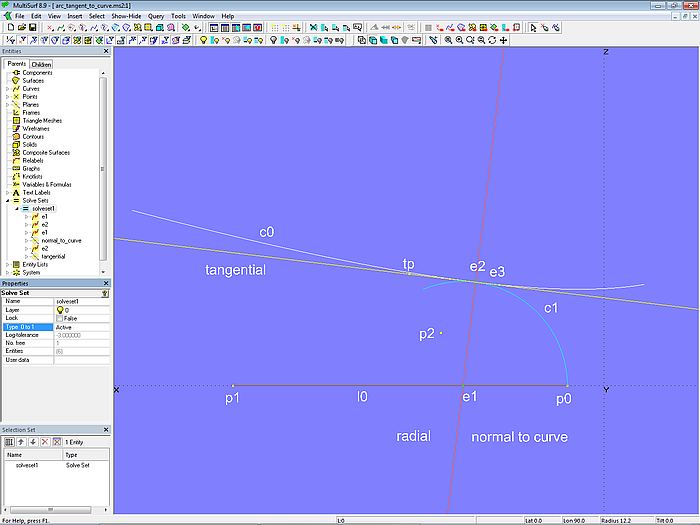
Modell arc_tangent_to_curve.ms2 – Solve Set solve_touch_curve aktiv
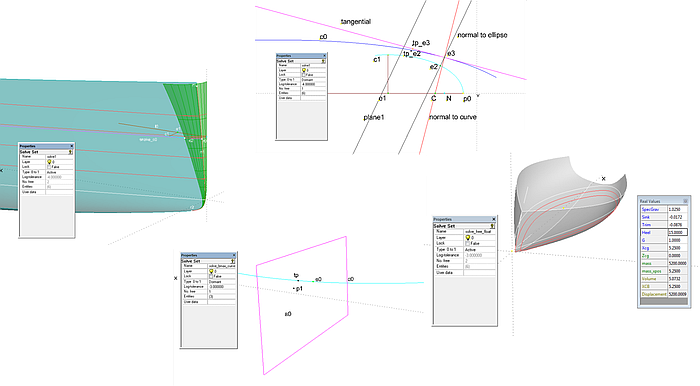
Aufgabe 4 – Ellipsenbogen berührt Kurve
Anstelle eines Kreisbogens soll ein Ellipsenbogen eine Wasserlinienkurve berühren. Diese Situation ist im Modell ellipse_tangent_to_curve.ms2 gezeigt.
Abgesehen von der Lage des Mittelpunkts gibt es bei einem Kreis nur eine Bestimmungsgröße, den Radius. Bei einer Ellipse gibt es dagegen zwei formbestimmende Größen, die große Halbachse und die kleine Halbachse. Darum muß ein Verhältnis zwischen den Halbachsen vorgegeben werden.
Manuelle Lösung
Im Modell ellipse_tangent_to_curve.ms2 gibt es die Kurve c0. Diese soll von der Ellipse c1 (Conic Section, Type = 1. Ellipse) berührt werden. Point p0 legt ihren Hauptscheitel fest. Die Strecke p0-e1 ist die große Halbachse, die kleine Halbachse ist die Strecke e1-p6. Das Längenverhältnis zwischen beiden Achsen bestimmt Variable b.
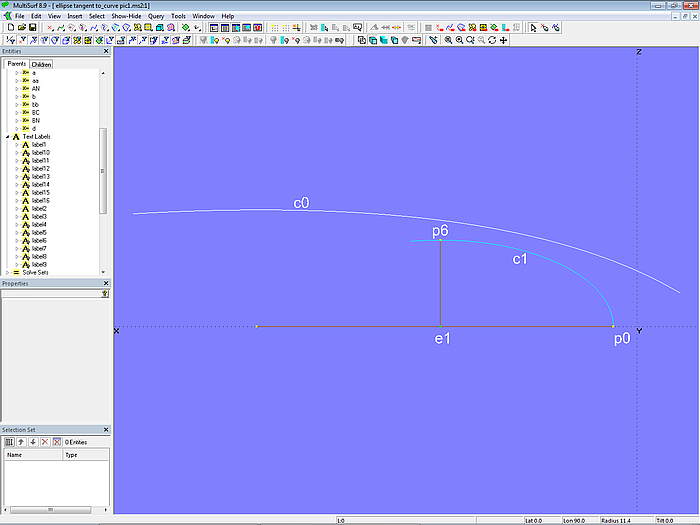
Modell ellipse_tangent_to_curve.ms2 – gesucht ist die Position des Beads e1, so dass der Ellipsenbogen c1 die Kurve c0 berührt. Hier ist die große Halbachse (Distanz p0-e1) noch zu kurz.
Durch Verschieben von Bead e1 kann man manuell die Position des Mittelpunktes finden, bei dem die Ellipse c1 die Kurve c0 berührt.
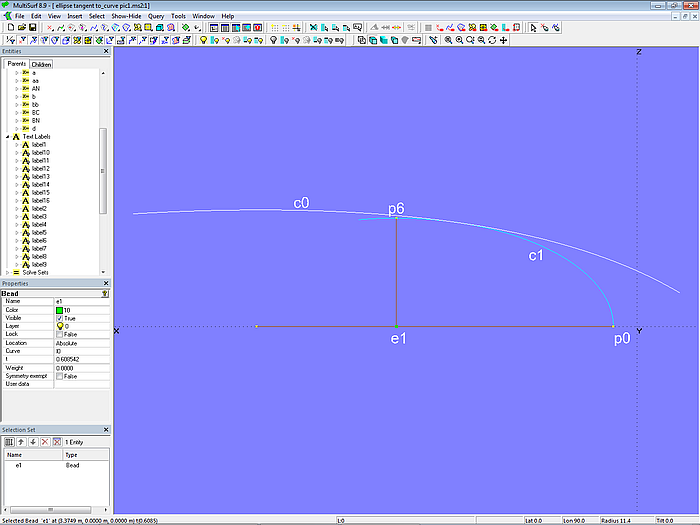
Modell ellipse_tangent_to_curve.ms2 – manuell ermittelte Position von e1,so das der Ellipsenbogen die Kurve berührt.
Soll die Berührung der Kurve durch den Ellipsenbogen eine dauerhafte Eigenschaft des Modells sein, muß ein Solve Set-Objekt verwendet werden.
Lösung mit Solve Set
Modell ellipse_tangent_to_curve.ms2 weist Ähnlichkeiten zum Modell arc_tangent_to_curve.ms2 auf. Auf dem Ellipsenbogen c1 (Conic Section, Type = 1. Ellipse) liegt Bead e2. Davon abhängig ist Tangent Point tp_e2. Mit beiden Punkten ist die 2-point Plane normal_to_ellipse bestimmt (Normale der Ellipse im Punkt e2). Diese Ebene schneidet die Kurve c0 im Intersection Bead e3. Dieser ist Support für den Tangent Point tp_e3. Mit beiden Punkten ist die 2-point Plane normal_to_curve definiert (Normale der Kurve c0 im Punkt e3). Diese Ebene schneidet Line l0 im Intersection Bead C. Mit e3 und C ist die 2-point Plane tangential erzeugt (Tangente der Kurve c0 im Punkt e3).
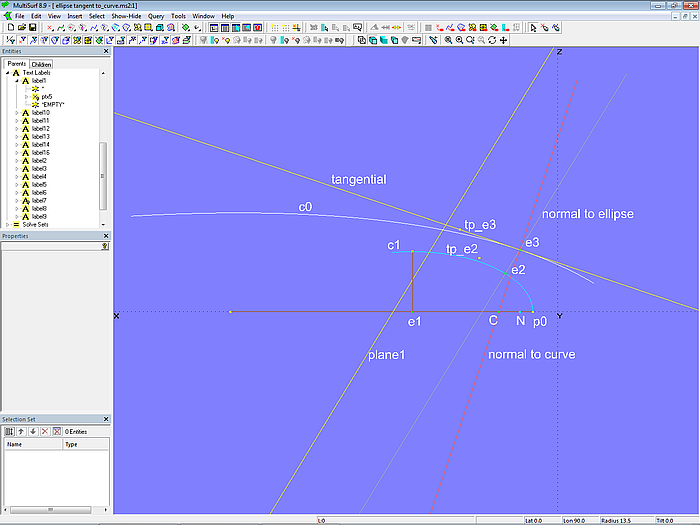
Modell ellipse_tangent_to_curve.ms2 – Solve Set solve_touch_curve inaktiv
Beim Kreis-Problem war die Bedingung für die Normale der Kurve c0 im Bead e3, dass sie durch den Kreismittelpunkt (Bead e1) geht. Dann ist sie gleichzeitig auch Normale an den Kreis. Beim Ellipsen-Problem verläuft die Normale aber nicht durch den Mittelpunkt, sondern schneidet auf der großen Halbachse die Subnormale sn ab.Darum gibt es zusätzlich die Offset Plane plane1, die durch den Ellipsenmittelpunkt M(mx;my) verläuft. Sie ist um den Offset-Wert d parallel zur 2-point Plane normal_to_ellipse.
Mit Hilfe der Beziehung für die Subnormale sn im Punkt P(px;py) läßt sich der Abstand d für diese Offset Plane ermitteln.
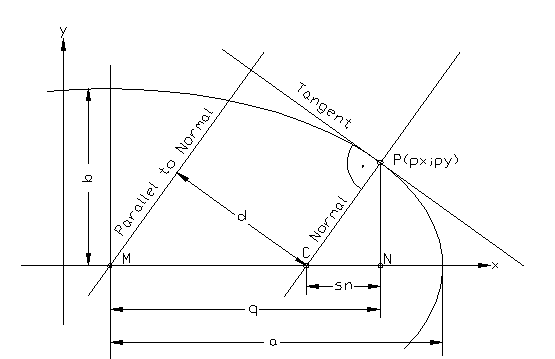
Ellipse – die Normale verläuft nicht durch den Mittelpunkt.
Für die Subnormale sn gilt:
sn = b2 / a2 * q
mit:
a – Länge große Halbachse
b – Länge kleine Halbachse
q – Abstand zwischen Punkt N und Mittelpunkt M
Desweiteren gilt:
d / MC = PN / PC
mit:
MC – Abstand zwischen Punkt C und Mittelpunkt M
PN – Abstand zwischen den Punkten P und N
PC – Abstand zwischen den Punkten P und C
Damit folgt:
d = PN / PC * MC
MC = q – sn
MC = q (1 – b2 / a2)>/p>
Also:
d = PN / PC * q (1 – b2 / a2)
Der Offset-Wert d für die Offset Plane plane1 wird mit Hilfe von Formula-Objekten berechnet.
Die freien Objekte des Solve Set-Objekts solve_touch_curve sind die Beads e1 und e2. Hat das freie Objekt Bead e1 von der Offset Plane plane1 den Abstand Null (Lösungsbedingung 1), und gleichzeitig das andere freie Objekte Bead e2 von der Ebene tangential auch den Abstand Null (Lösungsbedingung 2), dann stimmen die Normalen überein und die Kurven berühren sich.
Folglich lautet die Liste der für die Lösung erforderlichen Objekte des Solve Set solve_touch_curve: {e1; e2; e1; plane1; e2; tangential}.
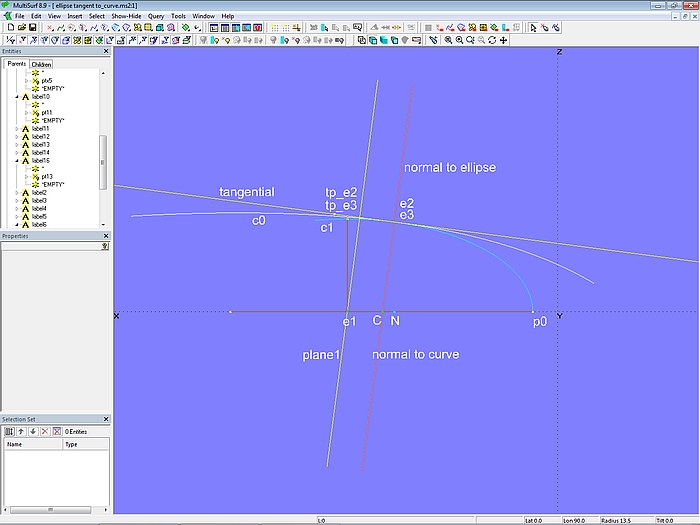
Modell ellipse_tangent_to_curve.ms2 – Solve Set solve_touch_curve aktiv
Wird die Kurve c0 geändert, findet der Solve Set automatisch den passenden Ellipsenmittelpunkt (Bead e1).
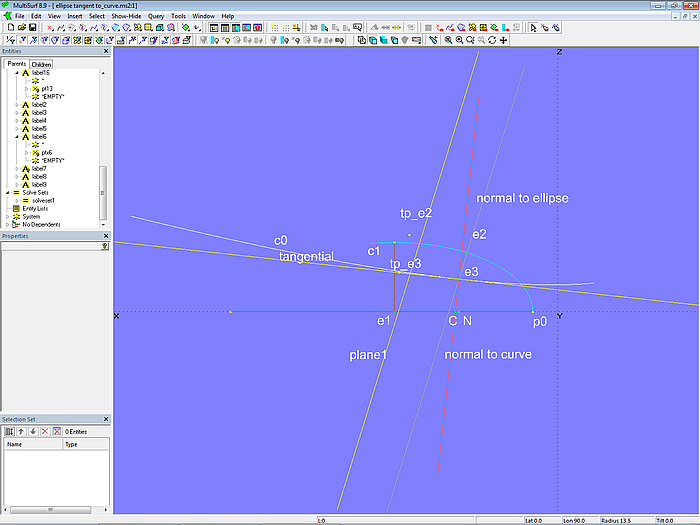
Modell ellipse_tangent_to_curve.ms2 – Solve Set solve_touch_curve inaktiv
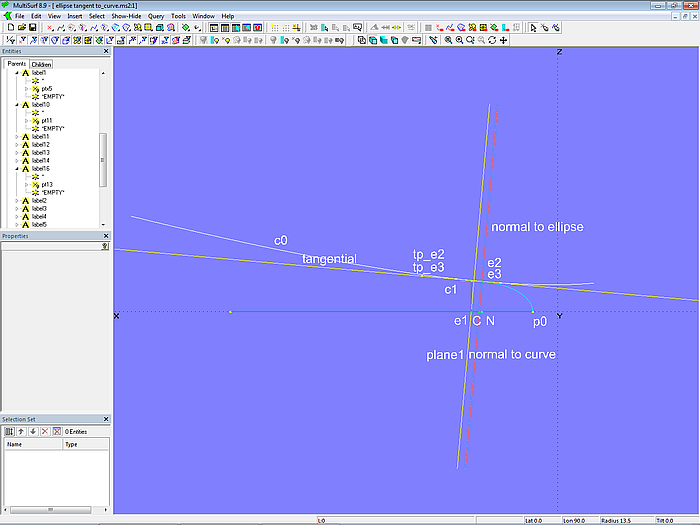
Modell ellipse_tangent_to_curve.ms2 – Solve Set solve_touch_curve aktiv
Bugrundung mit Ellipsenbögen
Modell sy15-elliptical_bowround.ms2 zeigt, wie mit der vorstehend gezeigten Methode der Vorsteven eines Rumpfes elliptisch abgerundet werden kann.
Entlang der Vorstevenkontur der Rumpffläche hull_0 verläuft die EdgeSnake n0. Auf dieser liegen die Ringe r1 und r2 und bestimmen die SubSnake n1. Auf n1 liegt Ring r0. Die Wasserlinie auf der Höhe von r0 ist die Intersection Snake snake_c0. Diese soll von der Ellipse c1 (Conic Section, Type = 1. Ellipse) berührt werden.
Der Aufbau der Berührkonstruktion ist im Prinzip der gleiche wie im Modell ellipse_tangent_to_curve.ms2, aber nun liegen snake_c0 und Ellipse c1 parallel zur XY-Ebene. Ring r0 wird auf die Mittschiffsebene projeziert als Projected Point p0 und ist Scheitel der Ellipse. Von p0 abhängig ist Line l0, auf der Bead e1 als Ellipsenmittelpunkt liegt.
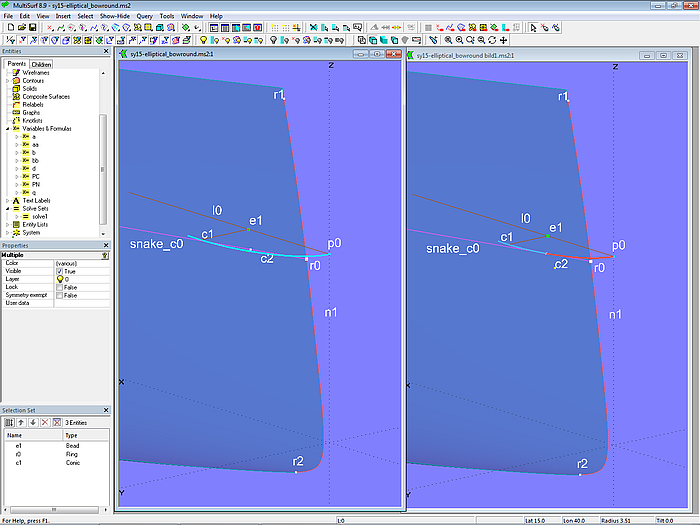
Modell sy15-elliptical_bowround.ms2 – elliptische Bugabrundung. Links: Solve Set solve_touch_wl inaktiv. Rechts: Solve Set solve_touch_wl aktiv.
Der Solve Set solve_touch_wl ermittelt die Position von e1, bei der Ellipse c1 die Wasserlinie snake_c0 berührt. Dieser Berührpunkt ist auf c1 der Bead e2, mit dem das Kurventeil bis zum Scheitel als SubCurve c2 definiert ist. Damit ist die elliptische Abrundung der Wasserlinie auf Höhe von r0 gefunden.
Verschiebt man Bead r0, verschiebt sich diese gesamte Konstruktion in Z-Richtung und SubCurve c2 überstreicht eine Fläche. Die Procedural Surface elliptical_bowround erzeugt diese Fläche.
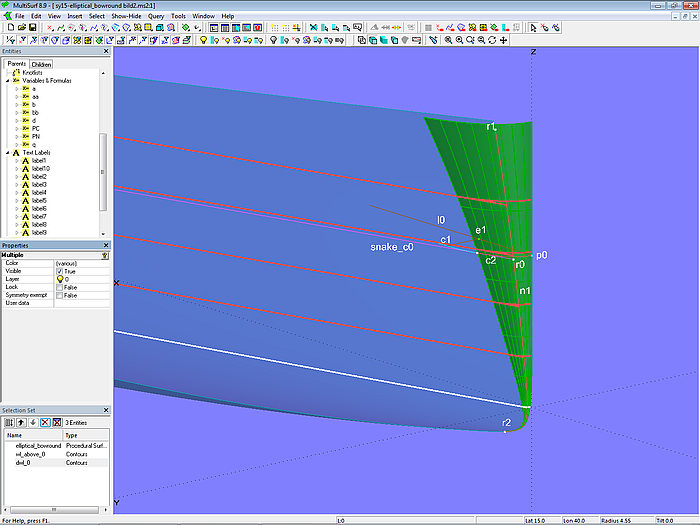
Modell sy15-elliptical_bowround.ms2 – elliptische Bugabrundung. Solve Set solve_touch_wl ist aktiv.
Weitere Solve Set-Anwendungen
Proximity Bead – Kreisbogen berührt zwei Kurven
Modell arc_tangent_two_curves.ms2 zeigt, wie sich zwei Kurven mit einem Kreisbogen mit gegebenem Radius ausrunden lassen. Dafür muß der Anfangspunkt des Kreisbogens Berührpunkt auf der einen Kurve sein, der Endpunkt des Kreisbogens Berührpunkt auf der anderen Kurve. Dies erfordert zwei freie Objekte, die so positioniert werden müssen, dass diese Bedingungen erfüllt sind.
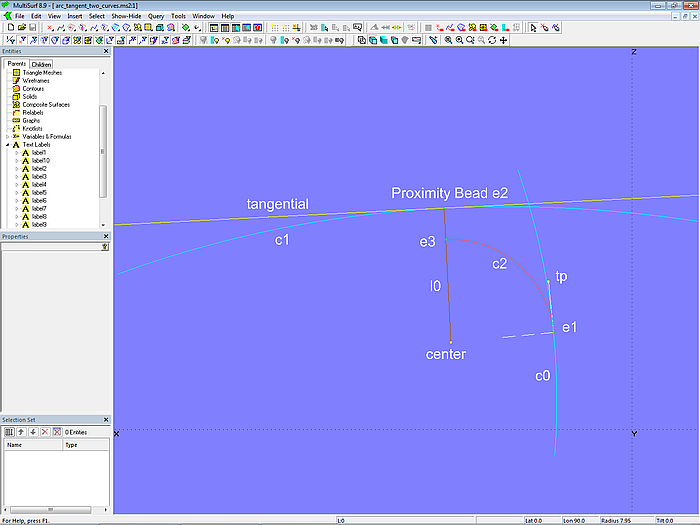
Modell arc_tangent_two_curves.ms2 –Kreisbogen c2 soll beide Kurve berühren; Solve Set solve_touch_curves nicht aktiv
Auf Kuve c0 liegt als Anfangspunkt des Kreisbogens Bead e1 (freies Objekt 1). Von e1 hängen Tangent Point tp und Point px (relativ zu e1 in Y-Richtung versetzt) ab. Mit diesen drei Punkten ist der 3-point Frame frame1 definiert. Die X-Achse von frame1 zeigt in Richtung des Tangent Point tp, ist also Tangente der Kuve c0 im Punkt e1. Die Z-Achse zeigt in Richtung der Normalen. Auf dieser Z-Achse, also der Normalen, liegt Point center, sein dz-Wert entspricht den Radius des Rundungsbogens.
Als Endpunkt des Kreisbogens liegt auf Kurve c1 der Punkt e2. Die Linie center-e2 ist Radiuslinie, also Normale der Kurve c1 im Punkt e2. Folglich muß Punkt e2 so positioniert sein, das er von center den kleinsten Abstand hat (freies Objekt 2). Mit einer speziellen Kurvenpunktart, dem Proximity Bead, läßt sich dieser Punkt einfach erzeugen. Ein Proximity Bead bestimmt denjenigen Punkt auf einer Kurve, der von einem außerhalb liegenden Punkt den kleinsten bzw. größten Abstand hat (je nach Einstellung).
Das freie Objekt 2 wird also durch den Proximity Bead festgelegt. Im vorliegenden Fall muß der Proximity Bead e2 vom Point center den kleinsten Abstand haben. Man kann auch sagen, der Proximity Bead e2 ist der Fußpunkt des Lots, das von center auf Kurve c1 gefällt wird. Mit den beiden Punkten center und e2 wird dann die 2-point Plane tangential erzeugt, also die Tangente der Kurve c1 im Punkt e2.
Line l0 verbindet center und Proximity Bead e2. Auf Line l0 liegt der Intersection Bead e3. Er hat von center den Abstand des Radius des Kreisbogens. Mit e1, center und e3 wird dieser Kreisbogen als Arc c2 erzeugt (Type = 2).
Gesucht ist nun die Position von e1 derart, dass der Abstand zwischen e3 und der Tangente tangential gleich Null ist, also der Kreisbogen c2 die Kurve c1 berührt. Zur Bestimmung dieser Position wird der Solve Set solve_touch_curves verwendet. Das freie Objekt ist Bead e1, das Objektpaar der Lösungsbedingung ist e3 und tangential. Folglich lautet die Liste der für die Lösung erforderlichen Objekte des Solve Set solve_touch_curves: {e1; e3; tangential}.
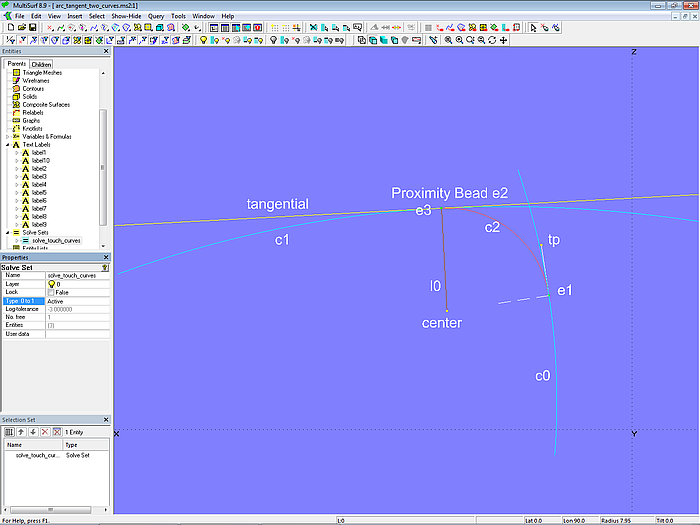
Modell arc_tangent_two_curves.ms2 – Solve Set solve_touch_curves aktiv; Kreisbogen c2 berührt beide Kurven.
Ändert sich die Form der Kurven, findet das Solve Set-Objekt automatisch den neuen Mittelpunkt der Ausrundung sowie Anfangs- und Endpunkt. Ebenso bei Änderung des Radius des Rundungskreisbogens.
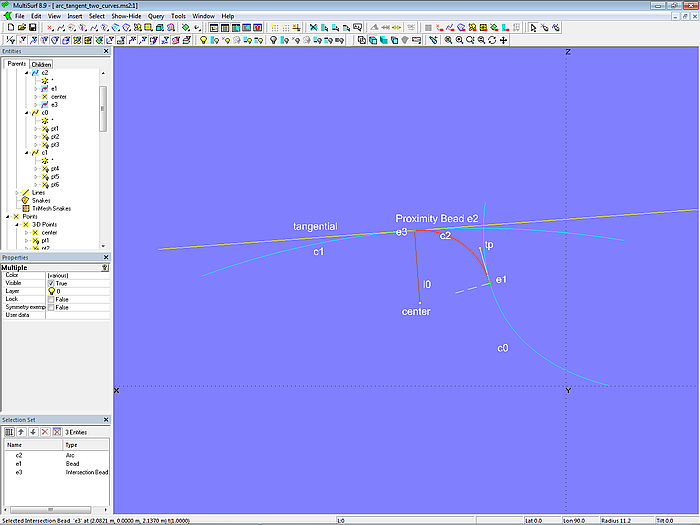
Modell arc_tangent_two_curves.ms2 – Solve Set solve_touch_curves aktiv; Kreisbogen c2 berührt beide Kurven.
Zwar läßt sich die hier gezeigte Konstruktion der Ausrundung auch ohne einen Proximity Bead durchführen, aber seine Verwendung macht das Modell einfacher und übersichtlicher. Mit dem Proximity Bead wird automatisch eines der beiden freien Objekte bestimmt.
Kreisbogen berührt Kurve - Version mit Proximity Bead
Wie sich auch die Konstruktionsaufgabe 3 – Kreis berührt Kurve – mit dem Objekt Proximity Bead vereinfachen läßt, ist in Modell arc_tangent_to_curve-Proximity_Bead.ms2 gezeigt. Es ist deutlich zu sehen, dass das Modell weniger Objekte erfordert.
Mittelpunkt des Kreisbogens c1 ist Bead e1 (freies Objekt 1). Davon abhängig ist der Proximity Bead e2 auf der Kurve c0; er hat von e1 den geringsten Abstand (freies Objekt 2). Line l1 verbindet e1 und e2, sie ist Radiuslinie des Kreisbogens und damit Normale der Kurve c0 im Punkt e2. Mit den beiden Punkten e2 und e1 wird dann die 2-point Plane tangential erzeugt, also die Tangente der Kurve c0 im Punkt e2. Der Kreisbogen c1 schneidet Line l1 im Intersection Bead e3.
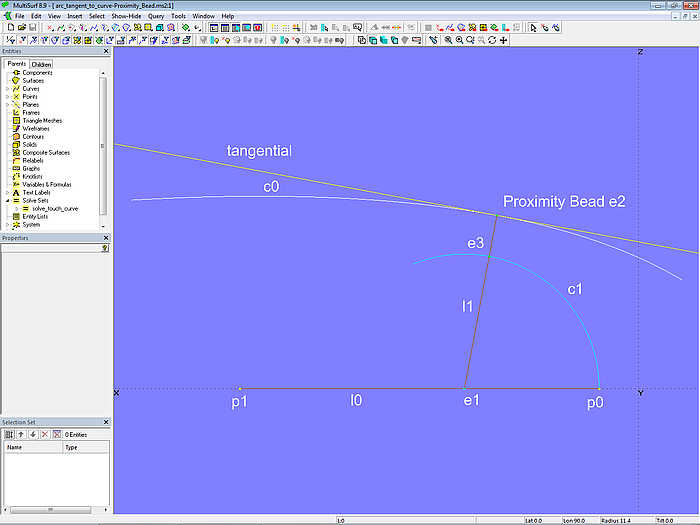
Modell arc_tangent_to_curve-Proximity_Bead.ms2 – Solve Set solve_touch_curve nicht aktiv
Die Position von e1 und damit der Radius (= Distanz p0-e1) muß so gewählt werden, dass der Abstand zwischen e3 und der Tangente tangential Null ist, also der Kreisbogen c1 die Kurve c0 berührt.
Zur Bestimmung dieser Position wird der Solve Set solve_touch_curve verwendet. Freies Objekt ist Bead e1, Objektpaar der Lösungsbedingung ist e3 und tangential. Die Liste der für die Lösung erforderlichen Objekte des Solve Set solve_touch_curve lautet also: {e1; e3; tangential}.
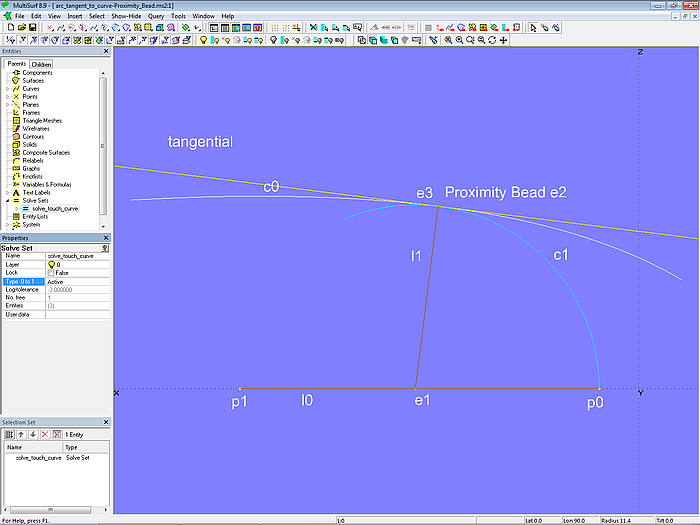
Modell arc_tangent_to_curve-Proximity_Bead.ms2 – Solve Set solve_touch_curve aktiv
Hydrostatik – freie Schwimmlage
Im Tutorium 14, „Rechnende Modelle in MultiSurf“ wird an Hand des Modells Hydro_free_floating.ms2 detailiert gezeigt, wie man mit dem Objekt Solve Set in Kombination mit Hydrostatic Reals die Frage beantwortet kann, welche Schwimmlage ein Bootsrumpf bei vorgegebenem Gewicht und Schwerpunkt einnehmen wird. Dazu ändert das Solve Set-Objekt solve_free_float systematisch Tauchung (Sink) und Trimm (Trim), bis ein Gleichgewicht zwischen den Kräften und Momenten von Gewicht und Auftrieb besteht.
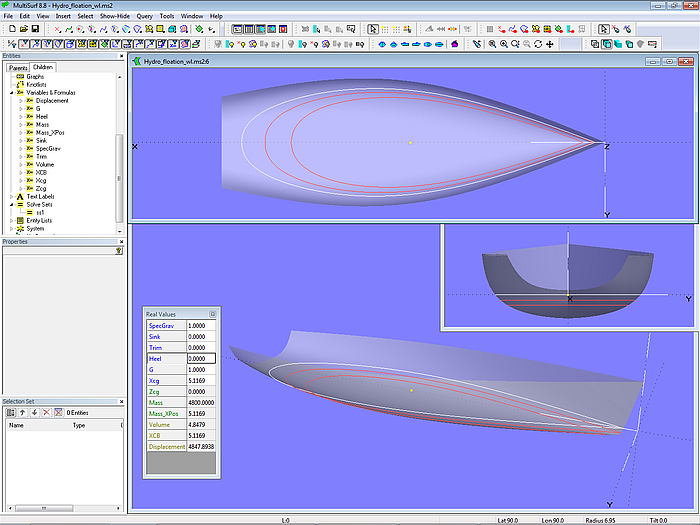
Modell Hydro_free_floating.ms2 – freie Schwimmlage bei Gleichgewicht von Gewicht und Auftrieb
Das Modell Hydro_free_floating.ms2 kann auch die Schwimmlage bei Krängung ermitteln. Das ermöglicht die Beurteilung der asymmetrischen Form der Wasserlinien oder die Beantwortung der Frage, ob der Spiegel frei von der Wasseroberfläche bleibt oder bereits eintaucht. Krängung bei festgehaltener Tauchung und Vertrimmung führt zu falschen Ergebnissen, da das verdrängte Volumen zunimmt. Um realistische Antworten zu erhalten, muß das Boot bei Krängung frei schwimmen.
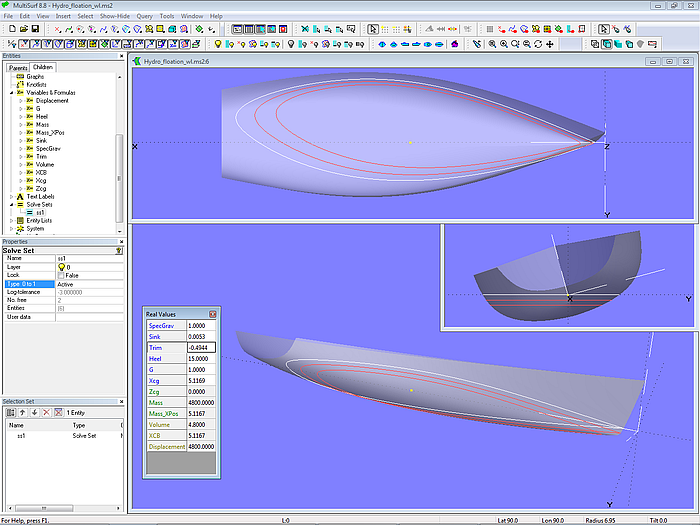
Modell Hydro_flotation.ms2 – freie Schwimmlage bei Krängung
Automatische Variation der Rumpfform
Tutorium 16, „Automatische Variation der Rumpfform“, befaßt sich mit der Problematik, dass beim Entwurf einer Rumpfform der Zeitpunkt erreicht wird, wo die Form den Vorstellungen entspricht, nur das Verdrängungsvolumen könnte beispielsweise ein wenig größer sein, und es wäre auch gut, wenn das LCB noch ein paar Zentimeter achterlicher wäre. Die Kontrollpunkte der Masterkurven müssen dann hier und da nur um wenige Milimeter verschoben werden, und neben den Hydrostatikwerten muß auch der Strak dauernd überprüft werden. Diese Feinarbeit ist zeitraubend.
Der im Tutorium 16 beschriebene Ansatz ermöglicht es, aus den Masterkurven eines vorhandenen Rumpfes automatisch neue Masterkurven zu generieren, so dass Sollwerte von Volumen und LCB erreicht werden. Dabei bleiben Strak, Außenkonturen des Rumpfes und Formcharakter der Mcs erhalten.
Im Modell formvariation_model-4.ms2 wird mit Hilfe des Solve Set-Objekts solve_V_LCB die Verschiebungskurve für die abgeleiteten Mcs automatisch so angepaßt, dass Volumen und Längenschwerpunkt der neuen Rumpfform den Vorgabewerten entsprechen.
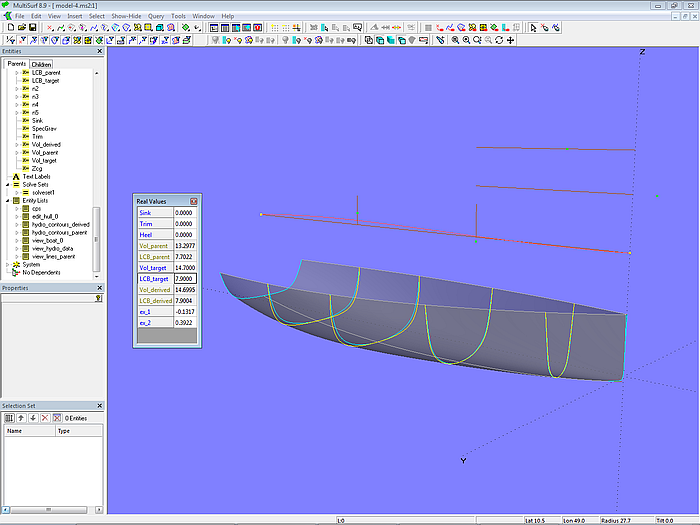
Modell formvariation_model-4.ms2 – größeres Volumen und LCB nach achtern verschoben
======================================================================================