Rundspantrumpf mit auslaufendem Knick
Eine weitere Variation der Rundspantbootsform
von Reinhard Siegel
Einleitung
Moderne Rennyachten zeichnen sich durch einen längslaufenden Knick im Rumpf aus. Bei einigen Booten verläuft der Knick in voller Länge vom Bug bis zum Heck, bei andere beginnt er achtern, verschwindet dann aber zum Vorschiff hin.
Dieser Artikel beschreibt an Hand des Modells sy15_vanish_chine.ms2, wie man in MultiSurf einen Rundspantrumpf mit auslaufendem Knick modellieren kann. Es geht dabei nicht um einen Rumpf mit spezifischen Abmessungen, sondern es soll eine in der Praxis erprobte Vorgehensweise gezeigt werden, damit man am Ende das auf dem Bildschirm sieht, was man sich vorgestellt hat.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point)
Mc: Masterkurve, Stützkurve (master curve, support curve)
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
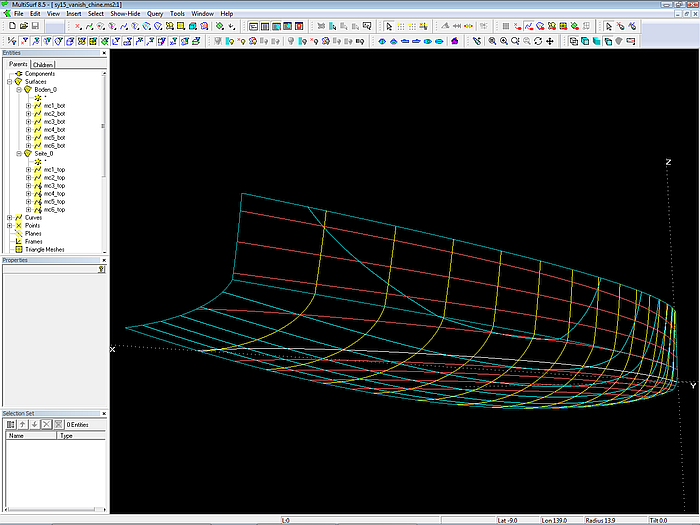
Modell sy15_vanish_chine.ms2
Konzept
Der Rumpf ist abgeleitet von den Modellen sy15.ms2 und sy15_full_chine.ms2, die in den Artikeln „Modellieren von Rundspantrümpfen“ und „Rundspantrumpf mit durchlaufendem Knick“ behandelt werden. Er besteht aus 2 längslaufenden Flächen, eine für die Seite, eine für den Boden. Sie werden analog wie bei einem Standard-Rundspanter erzeugt.
Beide Flächen – bottom_0 und topside_0 - sind C-spline Lofted Surfaces mit je 6 B-spline-Masterkurven. Die Mcs für die Bodenfläche sind vom Grad (Degree) = 3 und alle mit 4 Kontrollpunkten definiert, die der Seitenfläche haben alle 3 Cps und Grad = 2. Mit dieser Systematik läßt sich wieder die Vertexkurven-Methode zum Straken verwenden.
Der erste Cp einer Boden-Masterkurve dient auch gleichzeitig als 3. Cp der korrespondierenden Mc für die Seitenfläche, so daß die Mcs zusammenhängen. Vertexkurve vl3 beschreibt den Verlauf des Längsknicks.
Die hinteren Mcs (4, 5, ,6) von topside_0 und bottom_0 stoßen mit einen Knick aneinander, die vorderen Mcs (1, 2, und 3) müssen ohne Knick aneinander anschließen.
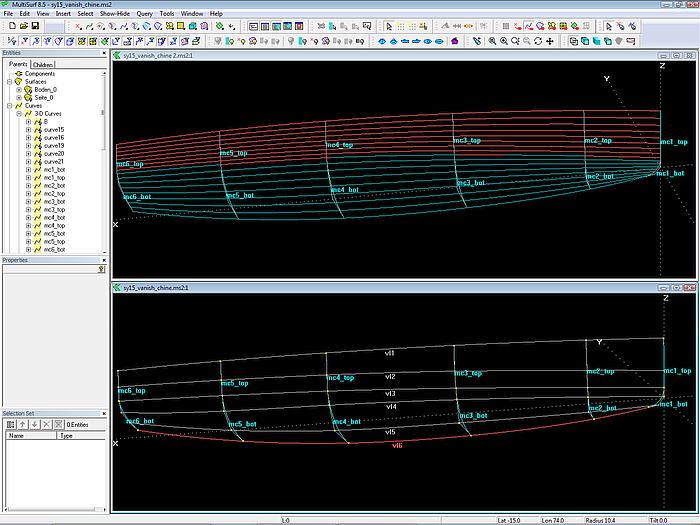
Modell sy15_vanish_chine.ms2 - je 6 Mcs stützen die C-spline Lofted Surfaces topside_0 und bottom_0. Vertexkurven verbinden korrespondierende Kontrollpunkte.
Wie verbindet man 2 B-spline Curves tangential?
Damit im Rumpf vorne kein Knick zwischen Seite und Boden auftritt, müssen die 3 vorderen Mcs für Seite und Boden tangential aneinanderstoßen. Dazu nutzen wir die Tangentialeigenschaft der B-spline Curve: sie beginnt immer tangential zur Linie zwischen dem 1. und 2. Cp und endet immer tangential zur Linie zwischen dem vorletzten und letzten Cp. Wenn also 2 B-spline Curves einen gemeinsamen End- bzw. Anfangspunkt haben, und seine beiden Nachbarpunkte liegen mit ihm auf einer Linie, ist der Übergang zwischen beiden Kurven glatt, ohne Knick.
Diese geforderte geometrische Bedingung zwischen den Kontrollpunkte cp2, cp3 und cp4 der vorderen 3 Masterkurven für Seite und Boden läßt sich auf folgende einfache Weise festverdrahten:
- man spannt eine Line auf zwischen den ersten beiden Cps der Boden-Mc
- und verwendet einen Bead auf diese Line als vorletzten Cp der Seite-Mc
Betrachten wir als Beispiel mc3_top und mc3_bot (Mc 3 für Seite und Boden): auf der Line line_3 zwischen Point p33 und Point p34 liegt der Bead p32_e. Alle 3 Punkte bleiben bei Änderungen ihrer Position stets auf einer Linie, und damit kann kein Knick zwischen beiden Mcs entstehen.
Alle Punkte cp2 der drei vorderen Mcs sind Beads; sie lassen sich auf ihrer Linie nur hin und her schieben. Diese Einschränkung garantiert aber die knickfreie Verbindung. Die Punkte cp2 der drei hinteren Mcs sind dagegen frei im Raum in alle Richtungen verschiebbare Punkte.
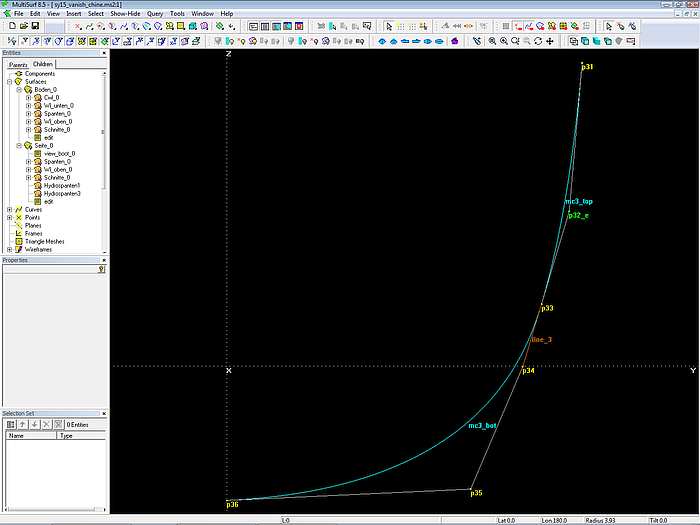
Modell sy15_vanish_chine.ms2 - B-spline Curve mc3_top schließt tangential an B-spline Curve mc3_bot an, wenn ihr gemeinsamer Kontrollpunkt p33 und seine benachbarten Punkte p32_e und p34 auf einer Linie liegen.
Warum die Linie zwischen p33 und p34 und nicht zwischen p32 and p34?
Der Bead p32_e liegt etwas jenseits des oberen Endes der Linie, aber in ihrer Verlängerung. Man könnte meinen, es wäre klarer, würde die Line zwischen den Punkten p32 und p34 verlaufen. Dann läge der Bead auf der Linie zwischen beiden Endpunkten.
Der Vorteil der hier gewählten Konstruktion ist aber, daß eine Verschiebung des Beads nur die Form der Seitenfläche des Rumpfes beeinflußt (über den Verlauf von mc3_top), während der Boden (über den Verlauf von mc3_bottom) sich nicht ändert. Würde die Line line_3 zwischen p32 und p34 aufgespannt, würden sich beim Verschieben des Beads beide Flächen gleichzeitig ändern. Es wird also eine unnötige Abhängigkeit vermieden.
Außerdem wird der Verlauf des Knicks durch alle Punkte cp3 bestimmt. Der Knick ist eine prominente Kurve und sollte deswegen direkt editierbar sein. Und nicht verändert werden infolge eines Nebeneffektes, wenn ein benachbarter Punkt verschoben wird.
Mit anderen Worten: die Seitenfläche des Rumpfes (topside_0) ist an die Bodenfläche (bottom_0) „angehängt“. Die Boden-Mcs und deren Kontrollpunkte spielen eine wichtigere Rolle für die Formgebung des Rumpfes als die Punkte cp2 der Seiten-Mcs.
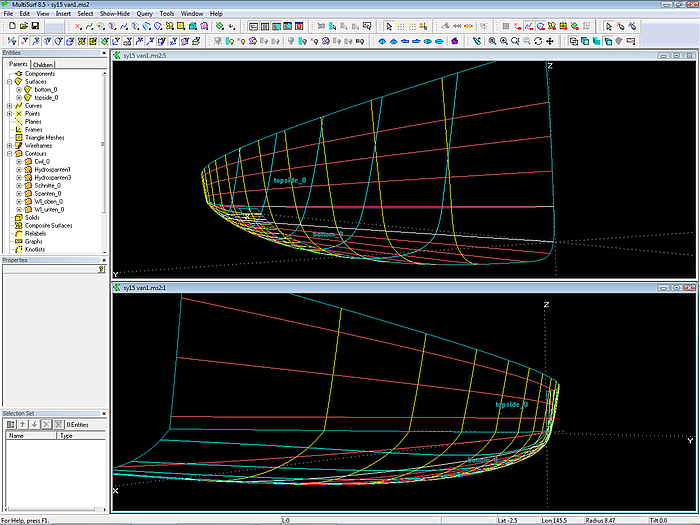
Modell sy15_vanish_chine.ms2 - auslaufender Knick; Perspektivansicht von vorn und von achtern
Obwohl in der Wireframe-Ansicht Spanten, Wasserlinien usw. auf dem ersten Blick ganz ok aussehen mögen, sollte man die Form auch in Render View überprüfen. Dabei zeigt sich ein Fehler: zwar ist die Seite mit dem Boden an den Mcs 2 und 3 glatt verbunden, aber nicht dazwischen.
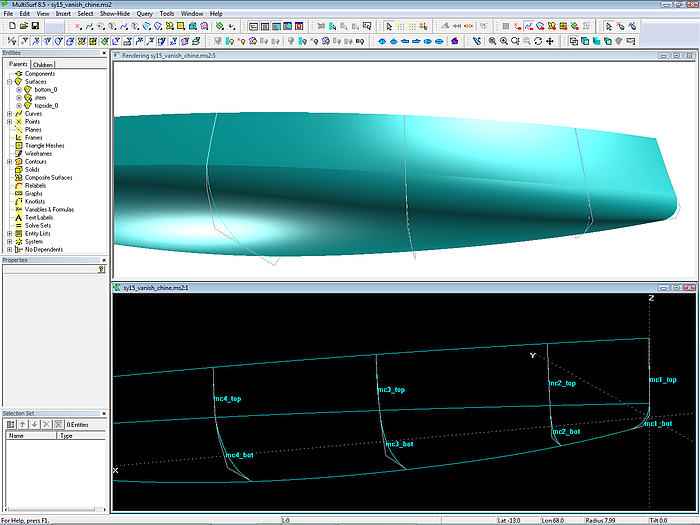
Modell sy15_vanish_chine.ms2 - Render View. Einbuchtung zwischen Seite und Boden im Bereich zwischen Mc2 und Mc3. Abhilfe durch Einfügen einer zusätzlichen Mc.
Dieser Fehler läßt sich durch eine kleinere Y-Koordinate von cp3 an Mc4 beheben, das heißt durch Verringerung der Breite des Knicks an Mc4. Aber nehmen wir an, Boden und Seite sollen nicht verändert werden - sie sind gut, wie sie sind. Dann ist die Lösung die, daß wir die obere Fläche auch zwischen Mc2 und Mc3 an die untere Fläche angeklammert werden – so, wie man es in der Praxis auch machen würde.
Das heißt, zwischen mc2_top and mc3_top muß eine weitere Mc eingefügt werden: mc2a_top.
Die Kontrollpunkte von mc2a_top sind leicht zu bestimmen: auf die Vertexkurve vl1 setzen wir einen Bead (e_vl1); er bestimmt die Längsposition von mc2a_top. An der Position von e_vl1 werden die Vertexkurven vl3 und vl4 geschnitten (XYZBeads e_vl3, e_vl4). Zwischen diesen beiden Beads wird eine Line gespannt und darauf der Bead e_vl2 gesetzt.
Mit diesen Beads e_vl1, e_vl2 und e_vl3 wird die neue B-spline Curve mc2a_top erzeugt. Außerdem wird zu den Kontrollpunkten der Vertexkurve vl2 noch der Bead e_vl2 hinzugefügt. Und schließlich mc2a_top als weitere Stützkurve für die C-spline Lofted Surface topside_0 eingefügt. Wir verklammern also die obere Fläche tangential mit der unteren an der Stelle des Beads e_vl1 auf vl1.
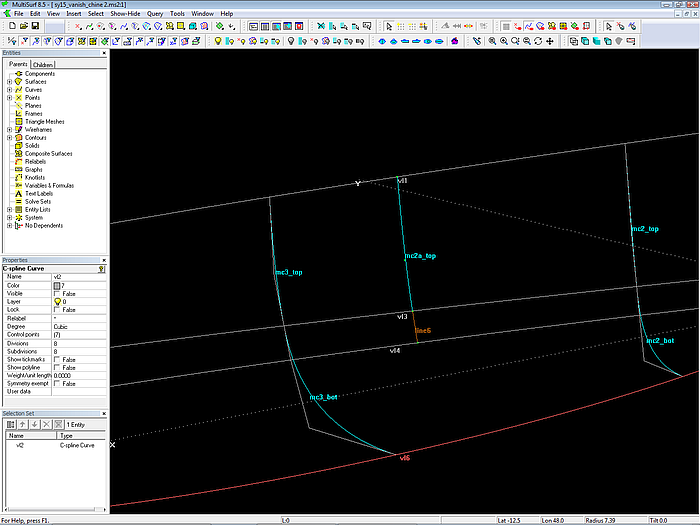
Modell sy15_vanish_chine2.ms2 – zusätzlich eingefügte Mc für die Seitenfläche des Rumpfes
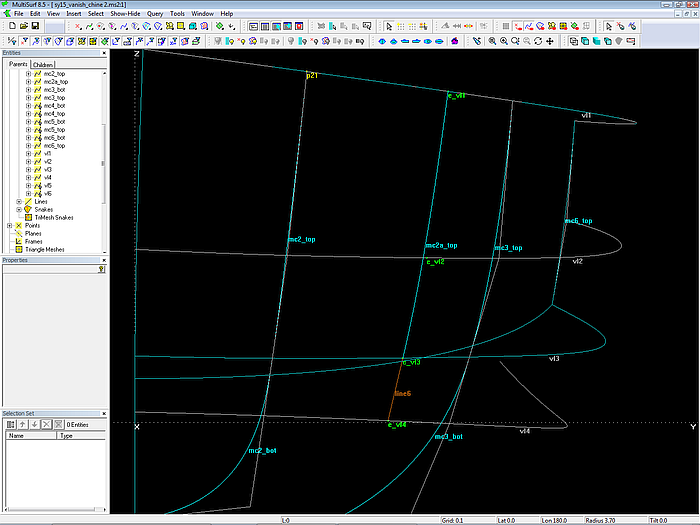
Modell sy15_vanish_chine2.ms2 – Konstruktion der 3 Kontrollpunkte für die zusätzliche Masterkurve mc2a_top
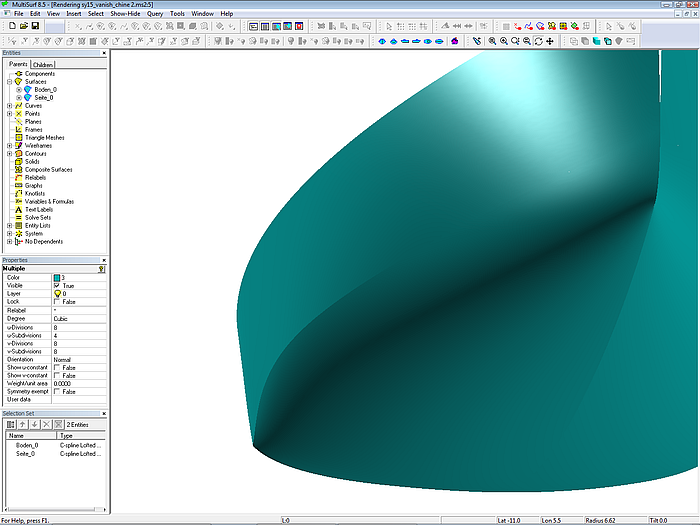
Modell sy15_vanish_chine2.ms2 – allmählich auslaufender Knick ohne Einbuchtung
Man beachte die Vorteile der Vertexkurven-Methode. Die Kontrollpunkte der zusätzlichen Mc mc2a_top sind keine freien Punkte, die sorgfältig und zeitaufwändig positioniert werden müssen, damit die Flächen straken. Sie ergeben sich aus den Vertexkurven. Durch die relationale Geometrie von MultiSurf braucht man nur den Bead e_vl1 auf der Vertexkurve vl1 zu verschieben, um die Position von mc2a_top festzulegen, sowie den Bead e_vl2 auf seiner Basislinie hin und her zu schieben, damit die Vertexkurve vl2 weiterhin strakt.
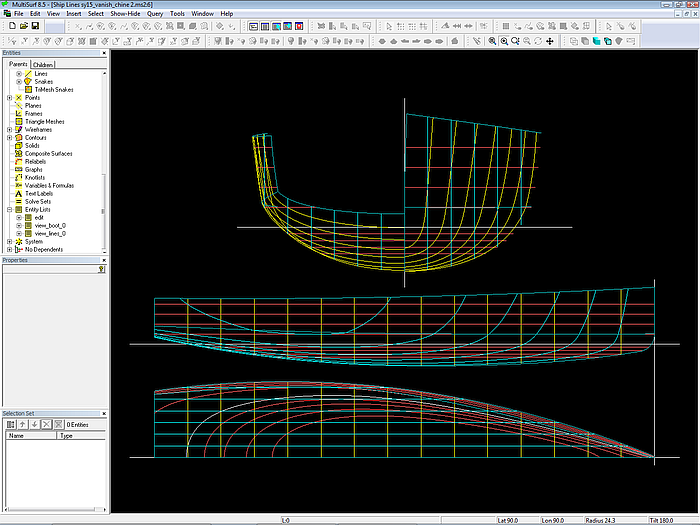
Modell sy15_vanish_chine2.ms2 – Ansicht Ship Lines
Krümmungsverlauf
Ein Problem gibt es aber noch: die 3 vorderen Mcs für die Seiten- und für die Bodenfläche sind zwar tangential miteinander verbunden, da wir dafür gesorgt haben, daß bestimmte Cps auf einer Linie liegen. Aber ist der Krümmungsverlauf entlang der beiden Kurven so, als wäre es eine einzige Kurve?
Um das zu überprüfen, setzen wir mc3_top und mc3_bot zusammen zur PolyCurve mc3_test und sehen uns ihr Curvature Profile an (View/ Display/ Profile/ Curvature oder Toolbar-Schaltfläche).
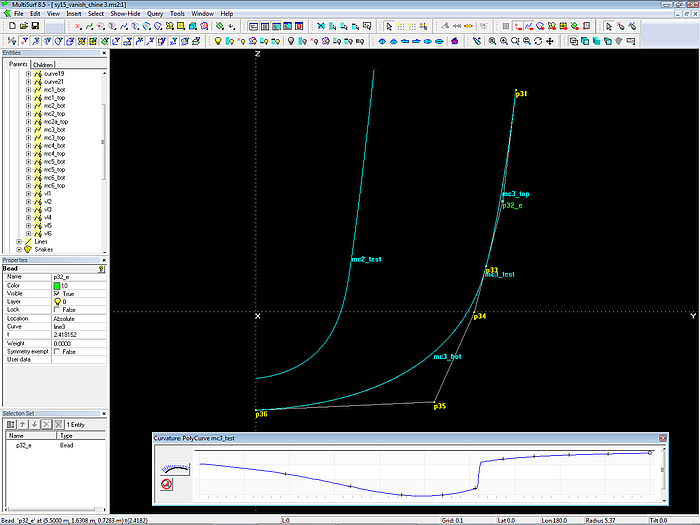
Modell sy15_vanish_chine2.ms2 - unharmonischer Verlauf der Krümmung entlang der PolyCurve mc3_test im Bereich des Übergangs der beiden Teilkurven mc3_top und mc3_bot.
Wenn man mit den Bead p32_e etwas verschiebt, läßt sich ein Verlauf erreichen, der dem einer durchgehenden B-spline Curve entspricht.
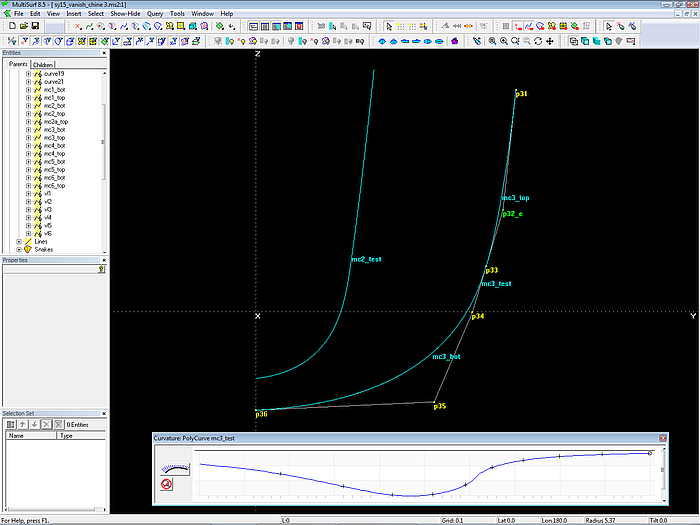
Modell sy15_vanish_chine2.ms2 - harmonischer Krümmungsverlauf der aus zwei Teilkurven zusammengesetzten PolyCurve mc3_test.
Ein Kontrollpunkt mehr für die Boden-Masterkurven?
Wenn wir uns ansehen, wie die Cps entlang der Boden-Masterkurven verteilt sind, zum Beispiel bei mc3, dann sehen wir, daß der Punkt p35 ziemlich weit entfernt ist vom Punkt p36. Deswegen ist hier die lokale Kontrolle über die Kurvenform ziemlich gering. Im Modell sy15_vanish_chine3.ms2 wurde in die Boden-Mcs ein weiterer Kontrollpunkt eingefügt.