Über Knickspantrümpfe für Motorboote
Eine weitere Variation des C-spline Lofted Surface-Themas
von Reinhard Siegel
Einleitung
Die Rumpfform von Motorbooten ist komplexer als bei Segelbooten. Knicke, Spritzkanten, Längsstufen in der Rumpfseite, Tunnel im Boden, Querstufen im Boden, um einige geometrische Formmerkmale zu nennen.
In diesem Artikel wird an Hand des Modells pb10.ms2 gezeigt, wie man in MultiSurf einen Knickspantrumpf für Motorboote modelliert. Dabei geht es nicht um einen Rumpf mit bestimmten Abmessungen, sondern es soll erklärt werden, wie die C-Spline Lofted Surface auch für diese Art von Rumpfform vorteilhaft genutzt werden kann.
Verwendete Abkürzungen:
Cp: Kontrollpunkt, Stützpunkt (control point, support point)
Mc: Masterkurve, Stützkurve (master curve, support curve)
cp1, cp2, ...: bezeichnet den 1., 2. ... Punkt in der Liste der Kontrollpunkte einer Kurve. Es ist kein Objektname.
mc1, mc2, ...: bezeichnet die 1., 2. ... Kurve in der Liste der Stützkurven einer Fläche. Es ist kein Objektname.
Im Folgenden werden die MultiSurf-Namen für Punkt-, Kurven- und Flächenarten verwendet. Das ergibt zwar „denglische“ Sätze, soll aber dem Verständnis und der Nachvollziehbarkeit dienen.
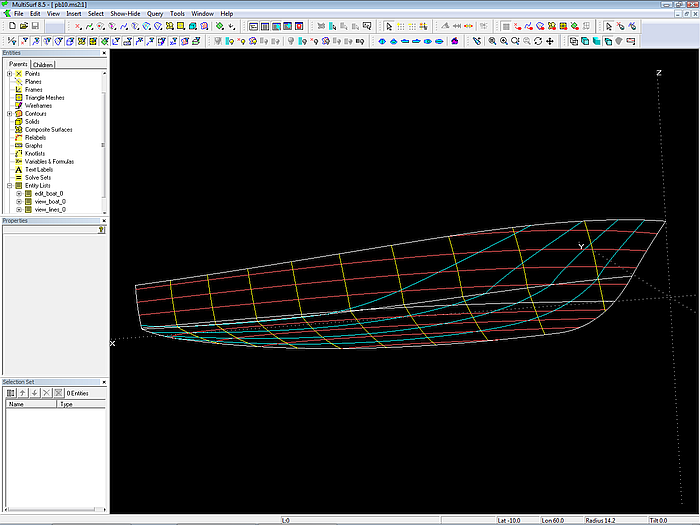
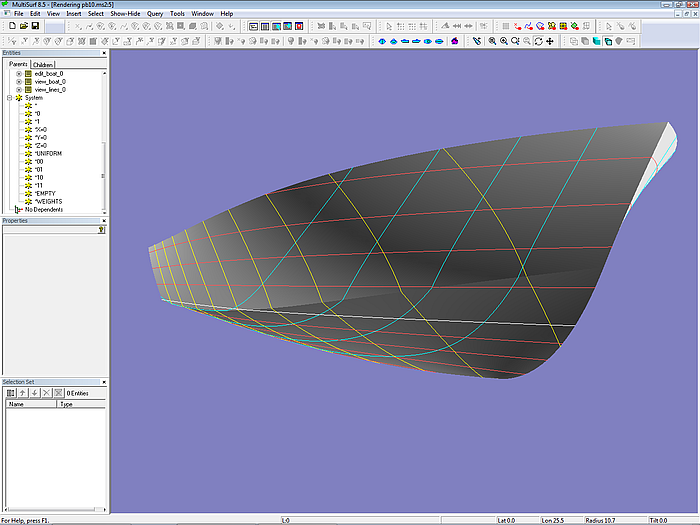
Modell pb10.ms2 - Wireframe-Ansicht
Konzept
Der Rumpf besteht aus 2 Flächen, Seite und Boden. Ihre Modellierung ist analog zu der eines Rundspantrumpfes. Beides sind C-Spline Lofted Surfaces, gestützt von je 6 B-spline-Masterkurven vom Grad 2. Jede Mc hat 3 Kontrollpunkte.
Der letzte Cp einer Mc für die Rumpfseite ist gleichzeitig auch der 1. Cp der entsprechenden Mc für den Boden. So fallen Unterkante der Seitenfläche und Oberkante der Bodenfläche zusammen - der zweiteilige Rumpf ist wasserdicht.
Die beiden Bug-Mcs (mc1_top, mc1_bot) sind strakend verbunden. Die anderen Mcs von Seite und Boden bilden dagegen einen Knick.
Vertexkurven (C-spline-Curves) verlaufen durch korrespondierende Cps.
Warum Vertexkurven?
Vertexkurven sind Hilfskurven zum Straken einer C-spline Lofted Surface. Verlaufen sie in harmonischer, regelmäßiger Weise, ist die Fläche glatt.
Die Vertexkurven-Methode erfordert, dass alle Mcs einer Fläche vom gleichen Kurventyp sind (hier: B-spline Curves) und jede Mc die gleiche Anzahl von Cps hat. Diese Bedingungen sind hier erfüllt.
Die Vertexkurve vl1 entspricht der Oberkante Rumpf, vl3 dem Knick und vl5 der Bodenkontur. Mit der Programmfunktion Display/ Profile/ Curvature läßt sich ihr strakender Verlauf leicht überprüfen.
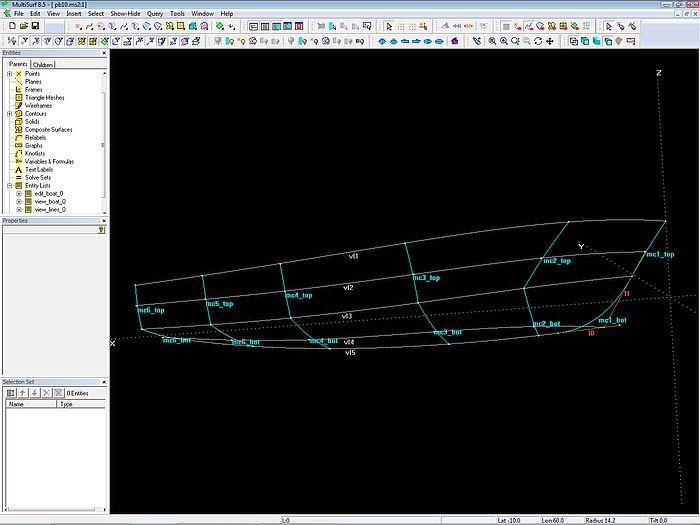
Modell pb10.ms2 - die C-spline Lofted Surface topside_0 und bottom_0 werden jeweils von 6 Mcs gestützt. Vertexkurven verlaufen durch korrespondierende Cps als Strakhilfen.
Warum in 3D straken?
Die Rumpfoberfläche muß glatt sein. Die Vertexkurven-Methode besagt: straken die Vertexkurven, dann strakt die Fläche. Folglich müssen die Cps der Mcs so angeordnet werden, daß die Vertexkurven glatt verlaufen. Das läßt sich sehr gut kontrollieren, in dem man sich diese Strakhilfskurven in 3D-Ansicht ansieht. Das Modell läßt sich auf dem Bildschirm um jeden beliebigen Punkt drehen, so daß man schräg entlang jeder Kurve schauen kann. Genau so, als hätte man ein echtes Modell gebaut und würde es in seiner Hand hin und her bewegen. Auf diese Weise läßt sich jede Unregelmäßigkeit im Verlauf einer Kurve, einer Wasserlinie etc. feststellen.
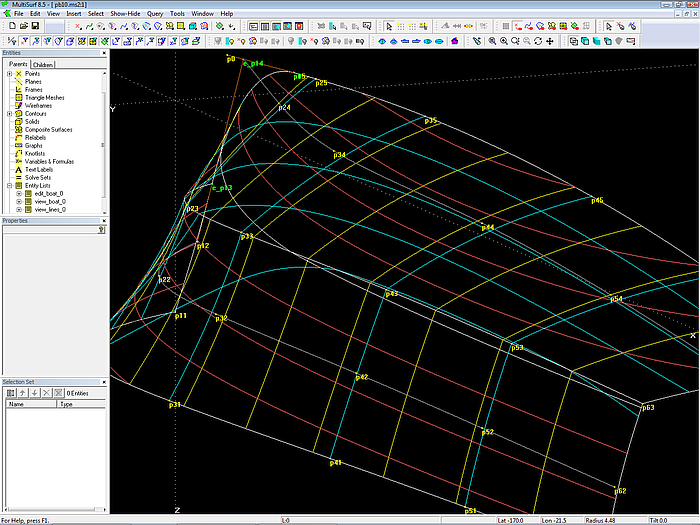
Modell pb10.ms2 - in der 3D-Ansicht läßt sich auf einfache Weise der strakende Verlauf von Kurven und Konturen überprüfen.
Warum das Verschieben von Cps einschränken?
Das Verschieben eines Punktes in der 3D-Ansicht ändert normalerweise jede seiner 3 Koordinaten. Über die Eigenschaft "Dragging" bei Punkten kann dies verhindert werden.
Um zum Beispiel sicherzustellen, dass alle Cps von mc3 bis mc6 in ihren Spantebenen bleiben, ist ihre Dragging-Eigenschaft auf (y and z) gesetzt. Wenn nun diese Punkte in 3D verschoben werden, ändern sich ihre X-Koordinaten nicht.
Weiterhin sollen alle Mcs der Bodenfläche auf der Mittschiffsebene enden. Daher ist für den letzten Cp die Y-Koordinate auf 0 gesetzt und seine Verschiebung nur in Z-Richtung erlaubt (Dragging: (z)).
Warum ist mc2_top geneigt?
Mc2_top verläuft nicht in einer Spantebene, seine 3 Cps sind versetzt angeordnet. Cp1 liegt vor cp2, und cp3 achterlich dahinter. Grund hierfür ist die Verteilung der Krümmung in der Rumpfseite. Der Bugbereich ist in der Aufsicht stark gekrümmt, braucht also hier mehr Unterstützung. Im Vergleich dazu ist der Knick weniger bogenförmig, so dass seine Stützpunkte weiter achtern liegen können.
Wie man die Bug-Mcs mc1_top und mc1_bot tangential verbindet
Der Vorsteven soll insgesamt eine harmonisch verlaufende Kurve sein, also darf zwischen der Mc für die Seite und der Mc für den Boden kein Knick sein. Um zwei B-spline Curves strakend zu verbinden, nutzen wir ihre Tangentialeigenschaft. Eine B-spline Curve beginnt immer tangential zum ersten Segment und endet immer tangential zum letzten Segment der Polylinie durch ihre Cps. Wenn also zwei B-spline Curves miteinander verbunden sind und die Nachbarpunkte zum gemeinsamen Punkt alle auf einer Linie liegen, ist der Übergang tangential.
Diese notwendige Beziehung für die Bug-Mcs läßt sich durch eine einfache Konstruktion fest verdrahten: a) zwischen dem 2. Cp der oberen Mc und dem 2. Cp der unteren Mc wird eine Line erzeugt; b) ein Bead auf dieser Line dient als 3. Cp der oberen Mc und als 1. Cp des unteren Mc, alle 3 Cps sind dann ausgerichtet.
Hinweis: geforderte geometrische Beziehungen sollten durch entsprechende Modellkonstruktion fest eingebaut werden.
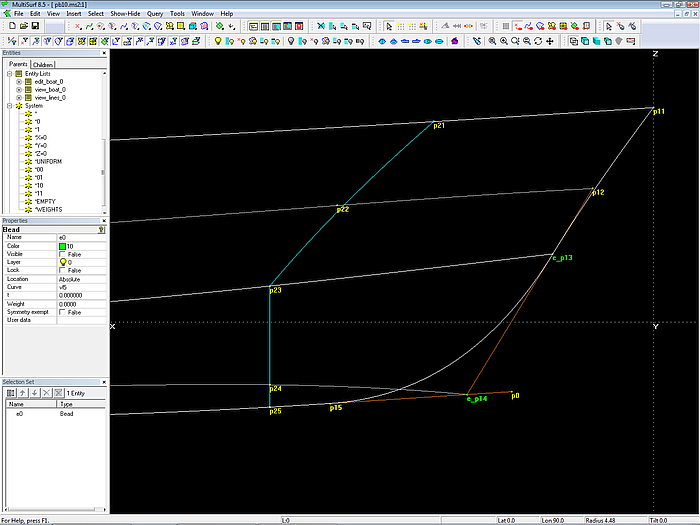
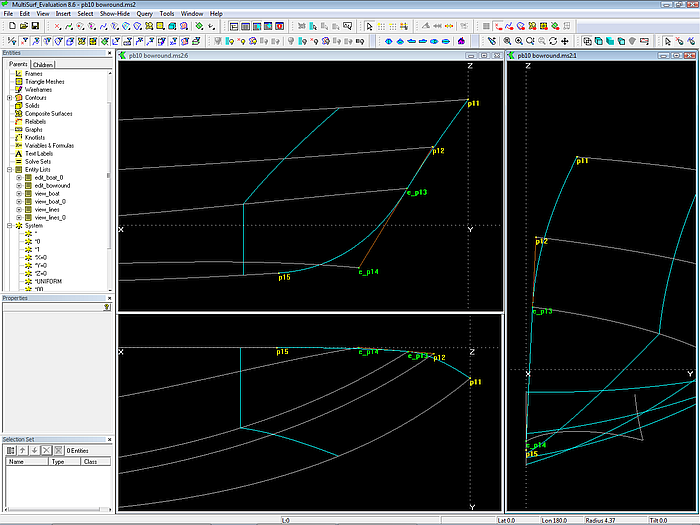
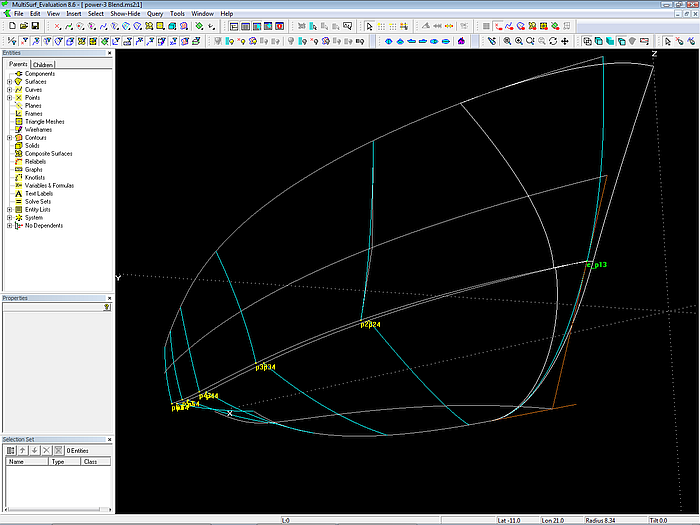
Modell pb10.ms2 – B-spline Curve mc1_top ist strakend mit B-spline Curve mc1_bot verbunden, wenn ihr gemeinsamer Kontrollpunkt e_p13 und seine Nachbarpunkte p12 und e_p14 auf einer Linie liegen. B-spline Curve mc1_bot endet tangential zur Vertexkurve vl5, weil vorletzter Cp (e_p14) und letzter Cp (p15) auf der Tangente im Anfangspunkt von vl5 liegen.
Wie der tangentiale Einlauf der Bug-Mc in die Bodenkontur verdrahtet ist
Die Vertexkurve vl5 beschreibt den Verlauf der Bodenkontur. Der Bug-Mc muss ohne Knick in diese Kurve einlaufen (es sei denn, es ist beabsichtigt). Man kann dies überprüfen, in dem man durch Zoomen und Drehen die Ansicht so einstellt, daß man schleifend entlang dem Ende von mc1_bot und dem Anfang von vl5 blickt.
Allerdings ist das keine dauerhafte Lösung. So wie etwas an der Form der Bug-Mc oder dem Verlauf der Bodenkontur geändert wird, muß man den Übergang zwischen beiden Kurven erneut prüfen und gegebenenfalls wieder manuell korrigieren.
Man löst das Problem in MultiSurf besser folgendermaßen. Wobei wir uns erneut die Tangentialeigenschaft von B-spline Curves zu Nutze machen. Zuerst benötigen wir eine Linie, die zu vl5 im Anfangspunkt tangential ist. Dazu erzeugen wir auf vl5 einen Bead mit t=0, darauf basierend einem Tangent Point und zwischen beiden eine Line. Dann setzt man einen Bead (e_p14) auf diese Tangentenlinie und verwendet ihn als cp2 der Bug-Mc mc_bot. Mit dieser einfachen geometrischen Konstruktion ist der tangentiale Einlauf der Bug-Mc in die Bodenkontur des Rumpfes im Modell fest verdrahtet.
Hinweis: geforderte geometrische Beziehungen sollten durch entsprechende Modellkonstruktion fest eingebaut werden.
Modell pb10.ms2 - Render view
Bugrundung
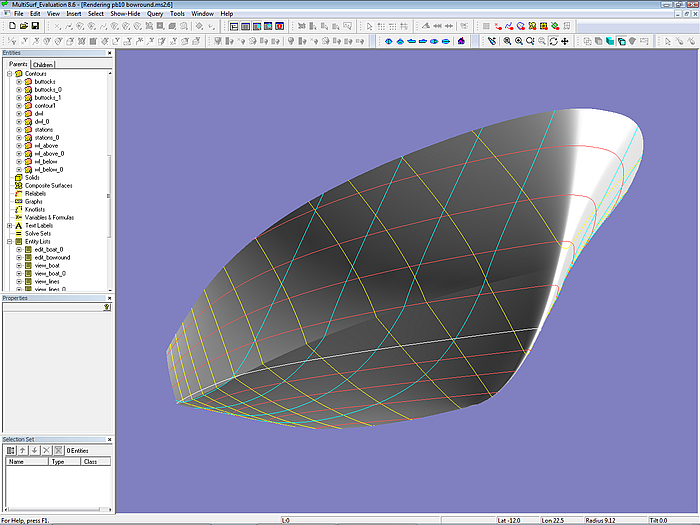
Bislang hat das Modell einen scharfen Vorsteven. Da die Y-Koordinaten ihrer Cps alle gleich Null sind, liegen die Steven-Mcs (mc1_top, mc1_bot) in der Mittschiffsebene. Es ist jedoch nicht weiter schwierig, eine Bugrundung hinzuzufügen. Dies wird im Modell pb10_bowround.ms2 gezeigt.
Konzept
Zunächst werden Kontrollpunkte der Bug-Mcs etwas von der Mittschiffsebene ins Positive verschoben. Der dadurch entstehende Spalt an den Vorderkanten von Seite und Boden wird durch Flächen senkrecht zur Mittschiffsebene geschlossen. Die Kanten zwischen Rumpf und diesen Stevenflächen werden dann abgerundet durch Blend Surfaces, die krümmungsstetig am Rumpf beginnen und immer normal zur Mittschiffsebene enden.
Dieser Ansatz ist analog zur Arbeit auf dem Reißbrett, wo man schwach und mäßig gekrümmte Kurven mit einer Straklatte zeichnete, aber in Bereichen, wo sie durch zu starke Biegung brechen würde, eine Kurvenschablone ansetzte (rohe und gekochte Spagetti-Technik).
Schritt 1:
Zuerst verschiebt man cp1 (p11) und cp2 (p12) von mc1_top etwas von der Mittschiffsebene weg (Y-Koordinate > 0). Man beachte, dass aufgrund der eingebauten geometrischen Beziehungen der knickfreie Übergang zwischen dem Bug-Mcs erhalten bleibt, ebenso der tangentiale Einlauf des Vorstevens in die Bodenkontur.
Modell pb10_bowround.ms2 – offener Bug durch Verschiebung von cp1 und cp2 der Bug-Mc der Seite weg von der Mittschiffsebene. Die tangentiale Verbindung zwischen den Mcs und der strakende Einlauf der unteren Bug-Mc bleiben durch die eingebauten geometrischen Beziehungen automatisch erhalten.
Schritt 2:
EdgeSnake le_topside_0 entlang der Vorderkante der Rumpfseite (topside_0) und Projektion auf die Mittschiffsebene (Projected Curve c0)
Schritt 3:
Ruled Surface top_flat_stem zwischen EdgeSnake le_topside_0 und Projected Curve c0
Schritt 4:
EdgeSnakes (in_top_flat_stem, out_top_flat_stem) entlang der Außen- und Innenkante der Ruled Surface
Schritt 5:
B-spline Snake n_start_round auf topside_0, wo die Bugabrundung beginnen soll
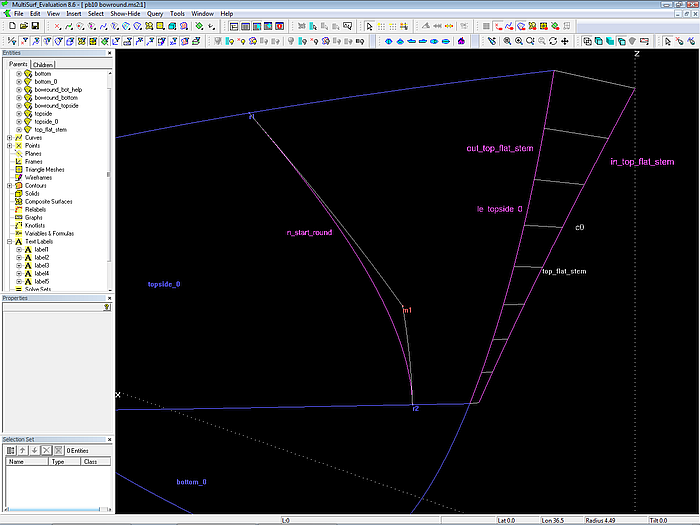
Modell pb10_bowround.ms2 - Ruled Surface top_flat_stem verläuft zwischen der Vorderkante (le_topside_0) der Rumpfseite und ihrer Projektion auf die Mittschiffsebene (Projected Curve c0)
Schritt 6:
Blend Surface bowround_topside mit Snake1: n_start_round, Snake2: le_topside_0, Snake3: out_top_flat_stem und Snake4: in_top_flat_stem
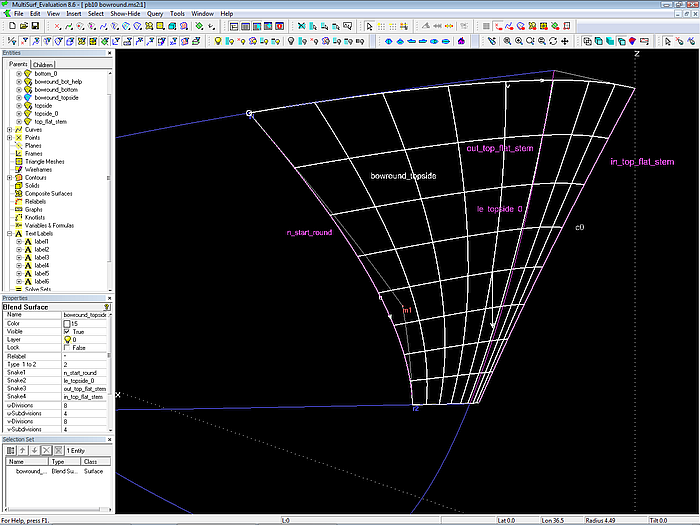
Modell pb10_bowround.ms2 – Bugrundung mit einer Blend Surface; sie beginnt krümmungsstetig auf der Seitenfläche (topside_0) und endet normal zur Mittschiffsebene.
Schritt 7:
SubSurface topside zwischen dem Beginn der Bugrundung (n_start_round) und der Hinterkante (te_topside_0) der Rumpfseite (topside_0).
Für die Bugrundung der Bodenfläche wiederholt man diese Schritte sinngemäß.
So wie das Modell auf diese Weise erstellt ist, kann es in seiner Form geändert werden. Die Bug_Mcs weiter von Mitte Schiff weg schieben, um die hier die Breite zu vergrößern, die Rundung weiter vorne oder weiter achtern beginnen lassen, dem Vorsteven mehr oder weniger Ausfall geben, gewölbter oder gerader Boden achtern, mehr Spantausfall in der Seite vorne, was auch immer – die in das Modell eingebauten geometrischen Beziehungen bleiben erhalten.
Warum Projektion der EdgeSnake und nicht von mc1_top?
Mc1_top ist eine Stützkurve für die Seitenfläche des Rumpfes. Sie verläuft entlang ihrer Vorderkante, ist aber keine Randkurve auf der Fläche selbst. Nur EdgeSnakes verlaufen entlang der Flächenkanten. In der Hierarchie der Abhängigkeiten gibt es zuerst mc1_top, dann die Fläche topside_0, dann die EdgeSnake. Wenn wir eine Stevenfläche am Bug anbringen wollen, ist es nach den Abhängigkeiten logisch, dafür die EdgeSnake an der Vorderkante als Kontrollkurve zu verwenden.
Angenommen, in einem späteren Stadium wird eine andere Kurve als Mc1 für die Rumpfseite verwendet. Dann muss man darauf achten, auch die Bugrundung entsprechend zu editieren. Mit der EdgeSnake wird der Bug automatisch angepasst.
Abgesehen davon – wenn der Aufbau des Modells nach einiger Zeit analysiert wird und man sieht, dass die Ruled Surface eine EdgeSnake als Kontrollkurve hat, weiß man gleichzeitig, dass sie wasserdicht an der Vorderkante der Seite anschließt. Ist die Stützkurve eine freie Kurve, so weiß man nur dies, erhält aber keine zusätzliche Information über die Geometrie des Modells und die Beziehungen zwischen ihren Bauteilen.
Die Kurvenart Line ist eine Linie, sie kann nur gerade sein. Eine B-spline Curve oder eine C-spline Curve kann ebenfalls vollständig gerade sein, aber das weiß man nur dann sicher, wenn man es nachgeprüft hat, und es z. B. nur 2 Cps gibt. Bei einer Line ist sofort klar, welche Eigenschaften zu erwarten sind.
Anmerkung: Der Punkt-, Kurven- und Flächentyp transportiert Informationen über die geometrischen Eigenschaften. Klare Informationen erleichtern die Arbeit.
Die Blend Surface erfordert 4 Snakes als Kontrollkurven, zwei auf Fläche 1 und zwei auf Fläche 2. Snake1 definiert den Beginn der Rundung auf Fläche 1, Snake4 bestimmt das Ende der Rundung auf Fläche 2. Die inneren Snakes (Snake 2 und Snake3) kontrollieren die Form der Rundung. Im vorliegenden Bespiel ist Snake2 die Vorderkante der Rumpfseite (topside_0) und Snake3 die Außenkante der Stevenfläche (top_flat_stem). Da beide Flächen durch den Modellaufbau eine gemeinsame Kante haben, verlaufen Snake2 und Snake3 übereinander (aber Snake2 liegt auf der Fläche topside_0, Snake3 auf der Fläche top_flat_stem).
Modell pb10_bowround.ms2 – Render view
Rumpf mit Spritzkante
Das Modell wird komplexer – es kommen 5 Punkte, 6 Kurven und 1 Fläche hinzu.
Konzept:
Bislang teilen sich Seitenfläche und Bodenfläche des Rumpfes eine gemeinsame Kante, denn cp3 der Mcs für die Seite ist gleichzeitig auch cp1 der Boden-Mcs (vom Bug abgesehen). Wird einer der cp3-Punkte verschoben, ändern sich also Oberseite und Unterseite des Rumpfes. Diese Verbindung wird getrennt, indem man einen eigenen cp1 für die unteren Mcs einfügt. Der Spalt zwischen der Unterkante der Seite und der Oberkante des Bodens wird dann durch die Spritzkante geschlossen.
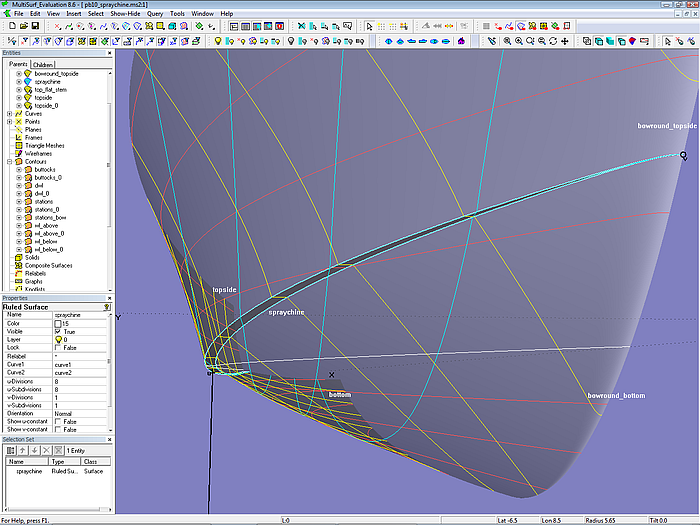
Modell pb10_spraychine.ms2 – die Masterkurven für die Seiten- und Bodenfläche haben am Kimmknick jeweils getrennte Kontrollpunkte. Deren Abstand kontrolliert die Breite der Spritzkante.
Die Spritzkante ist eine Ruled Surface, aufgespannt zwischen zwei PolyCurves. Die eine PolyCurve ist die Kombination der Unterkanten von Rumpfseite und ihrer Vorstevenrundung (EdgeSnakes). Die andere PolyCurve verbindet die Oberkanten von Rumpfboden und dessen Stevenabrundung.
Modell pb10_spraychine.ms2 – die Ruled Surface spraychine verbindet den unteren Rand der Seite mit der Oberkante der Bodenfläche. Shaded view.
Warum verläuft die Spritzkante zwischen PolyCurves?
Die Spritzkante schließt den Spalt zwischen den Flächen der Seite und den Flächen des Bodens. Entweder könnte man eine kurze Spritzkantenfläche zwischen Unterkante oberer Rundung und Oberkante unterer Rundung machen. Sowie einen langen Spritzkantenstreifen zwischen dem unteren Rand der Seite und dem oberen Rand des Bodens. Oder man macht die Spritzkante in einem Stück, verbindet also die Kombination der Kanten.
Der Autor bevorzugt das letztere Vorgehen, es ist eine Frage der persönlichen Vorliebe. Das kurze Stück Spritzkante zwischen den Bugrundungen könnte leicht vergessen werden, zum Beispiel bei der Auswahl der Flächen für Contours.
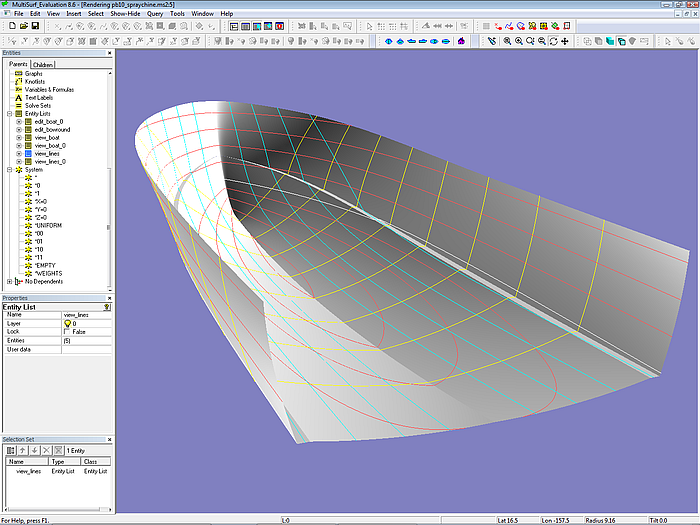
Modell pb10_spraychine.ms2 - Render view
Stufen in der Rumpfseite
Wenn wir schon dabei sind, dem Modell weitere Formmerkmale hinzuzufügen – wie wäre es mit Stufen in der Rumpfseite? Zum Beispiel als Aussteifung, Spritzkanten, Design-Marke.
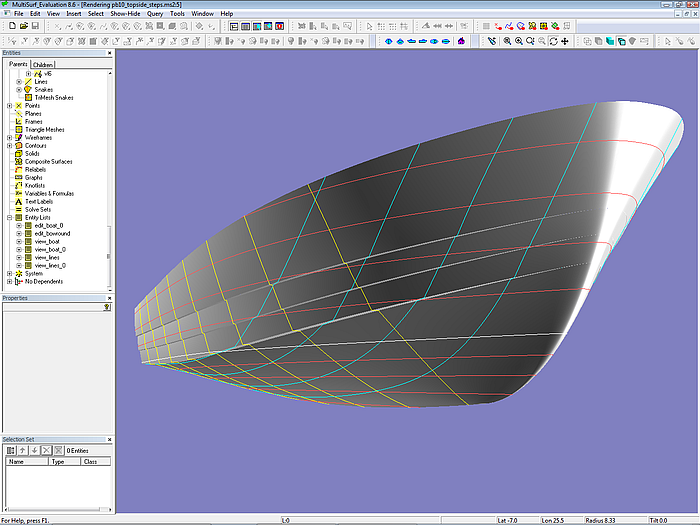
Modell pb10_topside_steps.ms2 – Render view
Konzept
Die Rumpfseite wird entlang der Stufenkanten in mehrere Längsstreifen aufgeteilt. Die horizontal orientierten Flächen sind wie die Spritzkante aufgebaut (Ruled Surface). Die vertikal verlaufenden Flächen sind eine weitere Anwendung der C-spline Lofted Surface. Jede hat eine eigene Bugabrundung (Blend Surface).
Modell pb10_topside_steps.ms2 – die Rumpfseite setzt sich aus 3 Flächen zusammen; jede Fläche ist eine C-spline Lofted Surface mit B-spline-Masterkurven.
Zum Vorsteven hin laufen die Stufen aus. Dies erfordert, dass alle Bug-Mcs der Seitenflächen strakend aneinander anschließen. Dazu nutzen wir wieder die Tangentialeigenschaft der B-spline Curve.
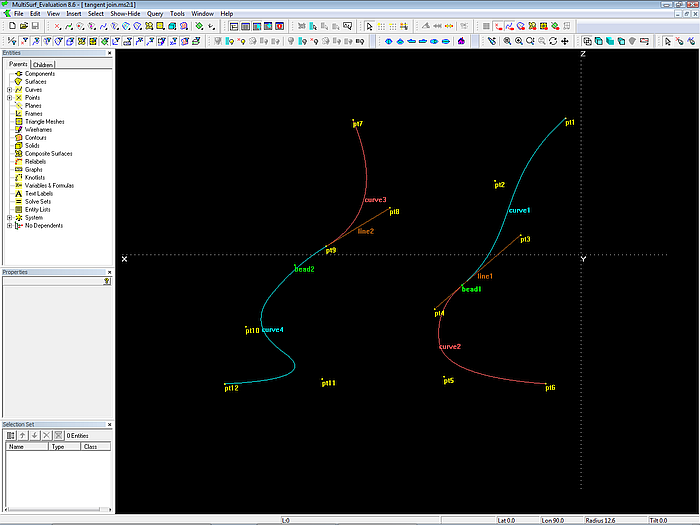
Modell tangent join.ms2 – das Prinzip der strakenden Verbindung zweier B-spline Curves: der gemeinsame Cp und seine beiden Nachbarn müssen auf einer Linie liegen.
Curve1 und curve2 teilen sich den gemeinsamen Cp bead1, der sich auf der Linie zwischen pt3 und pt4 befindet. In dieser Konstruktion ändert der gemeinsame Cp seine Position, wenn pt3 oder pt4 verschoben wird.
Curve3 und curve4 teilen sich den gemeinsamen Cp pt9, seine Nachbarn sind pt8 und bead2. Letzterer liegt auf der Linie zwischen pt8 und pt9 (genauer: auf der Verlängerung). In dieser Konstruktion ist der gemeinsame Cp frei zu positionieren.
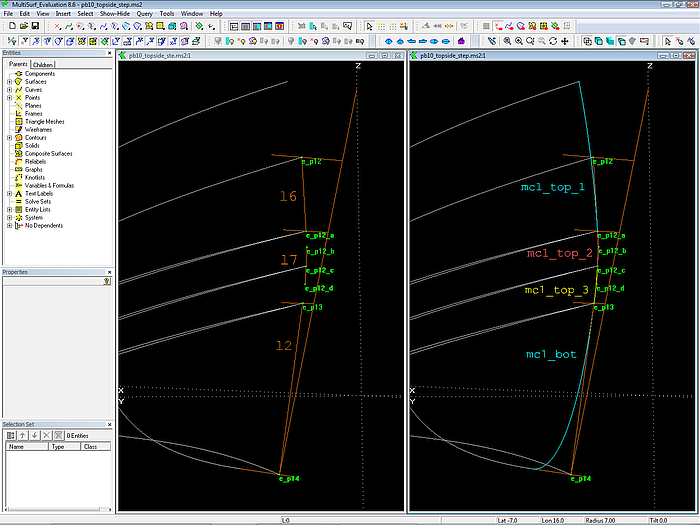
Modell pb10_topside_steps.ms2 – Konstruktion der tangentialen Verbindung der Bug-Mcs für die Flächen der Rumpfseite. Bead e_p12_b liegt auf Line l6, Bead e_p12_d auf Line l2 und Bead e_p12_c auf Line l7.
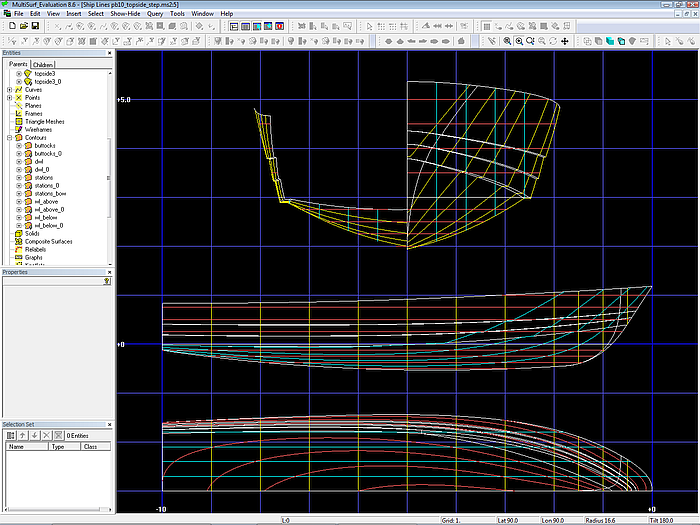
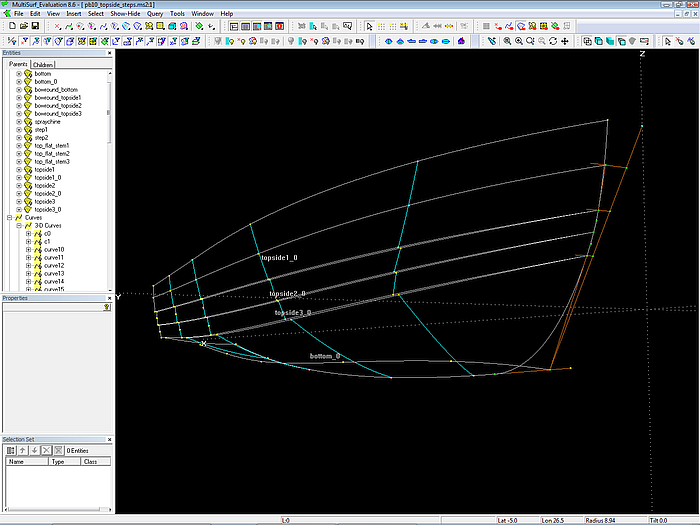
Modell pb10_topside_steps.ms2 – Ship Lines view
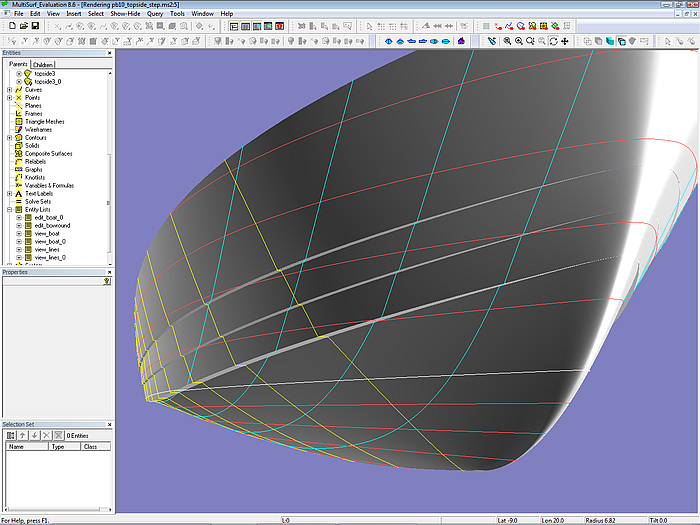
Modell pb10_topside_steps.ms2 – Render view
So weit zu den Grundlagen der Konstruktion von Geometriemodellen für Knickspantrumpfformen für Motorboote.
=====================================================================================